Если вместо двух диэлектрических сред – граница раздела металл (идеально проводящий) и диэлектрик, то .
Тогда R^= -1; T^= 0; y^= p;
Rêê= 1; Têê= 0; yêê= 0;
при любом угле падения j.
Структура поля в первой среде та же,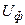 
и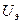 
– не меняются, а во второй среде поля нет.
На границе раздела с поглощающей средой можно воспользоваться полученными выражениями, если предположить, что b2 – комплексная величина: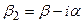 
.
Тогда sinq – тоже комплекс, то есть q – не геометрический угол, под которым распространяется преломлённая волна.
Введём обозначения:
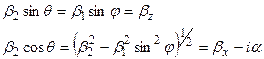
a, bx, bz – вещественные.
Для нормально поляризованной волны:
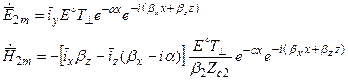
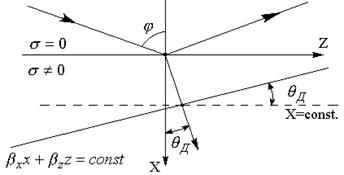
То есть в поглощающей среде – поле – плоская волна и если j ¹ 0 – неоднородная.
Поверхности равной амплитуды:
Х = const.
Поверхности равной фазы:
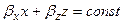
Во второй среде направление распространения образует угол qД с осью x.
qД - истинный (действительный) угол:
.
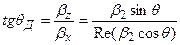(волна расположена перпендикулярно поверхностям равных фаз).
Во второй среде амплитуда убывает по экспоненте, причём во второй среде есть продольная составляющая.
Для параллельной поляризации то же самое.
Практически важный случай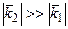 
.
Например, металлы: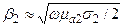 
, тогда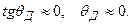 
То есть при любом угле падения j на поверхность хорошо проводящей среды преломлённая волна распространяется практически вдоль нормали к границе раздела.
Плоскости равных фаз и амплитуд практически совпадают - волна однородная.
Волна - поперечная, причём Е и Н сдвинуты по фазе на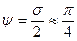 
.
Так как амплитуда быстро убывает, то поле есть практически в тонком поверхностном слое (явление поверхностного эффекта).
По закону Ома: J = dE, весь ток сосредоточен возле поверхности. Эффективное сечение меньше геометрического, а активное сопротивление на ВЧ может быть во много раз больше, чем по постоянному току (проводник можно выполнить в виде трубы).
Используют математическую модель, полагают, что ток течёт в виде бесконечно тонкого слоя:
,
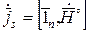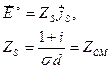
ZСМ - поверхностное сопротивление проводника, d - глубина проникновения.
Это выражение было получено на основе граничных условий Леонтовича–Щукина.
Особенность в том, что они выражают соотношение между векторами электромагнитного поля вблизи границы с реальными металлическими телами через параметры металла, без учёта поля в нём.
Мы уже определили, что в хорошо проводящей среде поле распространяется вдоль нормали к границе раздела:
.
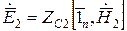На границе раздела:
.
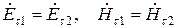Векторы Е и Н параллельны границе раздела, следовательно:
,
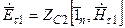так как
,
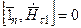то вместо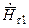 
можно использовать полный 
:
.
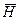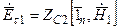На поверхности реального проводника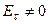 
и, хотя она очень мала ( 
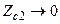), она определяет нормальную составляющую П (поток энергии, уходящий в металл).
Составляющую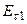 
в расчётах учитывают только тогда, когда рассчитывают потери.
Если граница раздела не плоская, то дополнительное условие - радиус кривизны должен превышать глубину проникновения.