От границы раздела обычных диэлектриков волна с нормальной поляризацией отражается всегда.
Волна с эллиптической поляризацией отражается от границы всегда.
Угол полного внутреннего отражения
Отметим условия, при которых вещество полностью отражает падающие на него электромагнитные волны.
Например, если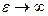 
при конечном m, то коэффициенты отражения стремятся к предельным значениям:
Rêê = - 1;
R^ = 1.
К этому предельному случаю очень близко подходят металлы, у них e имеет большую мнимую часть. Металлы - почти идеальные зеркала для электромагнитных волн.
Если существуют вещества, у которых при конечной e, m была бы весьма велика, то для них:
Rêê=1;
R^= -1.
÷ R ç стремится к 1 для критической плазмы (e £ 0).
Рассмотрим более подробно второй закон Снелля
Угол q меняется от 0 до p/2 (p/2 – предельное значение).
Угол падения, при котором q = p/2, назовём критическим:
,
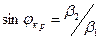это возможно, если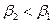 
.
При j > jкр правая часть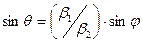 
становится больше единицы. Если q – вещественный, это невозможно.
Будем полагать: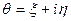 
.
Тогда: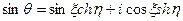 
.
Чтобы sin q >1 достаточно: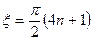 
и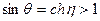 
, а cosq – мнимый.
С учётом этого при любом h ¹ 0:
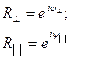
То есть средняя плотность потока энергии одинакова в падающей и отражённой волнах.
Поле в первой среде (после того, как за скобки вынесли exp(iy^/2)):
;
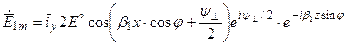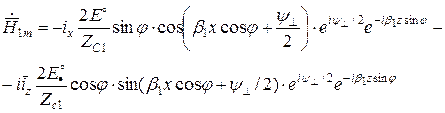
Итак, в первой среде ЭМП имеет структуру плоской волны, распространяющейся вдоль поверхности раздела (вдоль z) – направленная волна.
Поверхности равных фаз – плоскости, перпендикулярные Z.
Амплитуды E и H зависят от X и от j.
Поверхности равных амплитуд–плоскости, перпендикулярные X.
Эта волна - неоднородная плоская волна, у которой есть продольная составляющая Hz .
(для волны с параллельной поляризацией–Ez).
Фазовая скорость:
,
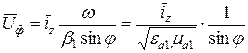то есть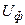 
больше 
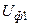, но меньше 
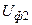. Причём, чем больше j, тем меньше .
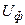Длина волны вдоль Z: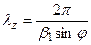 
.
Изменение Е и Н вдоль оси Х имеет характер стоячей волны в первой среде: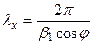 
.
Поперечные составляющие изменяются в фазе, а продольная сдвинута на 90°, в результате комплексный вектор Пойнтинга:
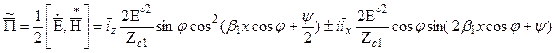
Знак ’+’ – перпендикулярная поляризация.
Знак ‘_’ - параллельная поляризация.
В среднем энергия распространяется только вдоль оси Z, а в перпендикулярном по отношению к Z направлении – только реактивный поток энергии:
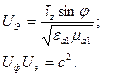
Рассмотрим поле во второй среде:
Так как cos q – мнимая величина, то:
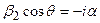
где
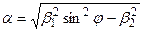
при j > jкр a – вещественная величина.
Знак ’’–’’ чтобы поле не росло до бесконечности (невозможно физически).
Для поля во второй среде:
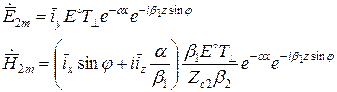
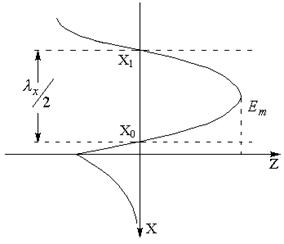Итак, во второй среде электромагнитное поле имеет структуру плоской неоднородной волны, распространяющейся вдоль оси Z.
Поверхности равной фазы и амплитуды взаимно перпендикулярны.
Энергия распространяется в среднем вдоль z, а вдоль x она убывает по экспоненциальному закону.
Такую волну называют поверхностной.
Любая из поверхностей Xn = const могла быть заменена на металлическую – это не изменит картины.
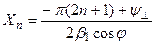
Поток энергии на плоскостях Xn = const - отсутствует (n = 1,2...).