Падение плоских электромагнитных волн на границу раздела двух сред
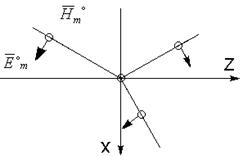
Границу раздела будем полагать бесконечно протяженной. Плоскость, проходящая через нормаль к границе раздела параллельно направлению распространения, называют плоскостью падения.
Если вектор Е перпендикулярен этой плоскости, то волна – нормально поляризованная, если параллелен, волна – параллельно поляризованная.
Любую другую ориентацию вектора Е следует рассматривать как суперпозицию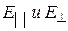 
.
Нормальная поляризация.
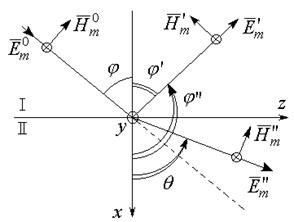j- угол падения.
В выбранной системе координат направляющие косинусы:
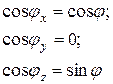и
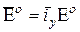
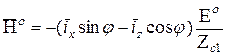
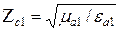
Для амплитуд:
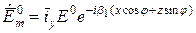
при условии 0³Х
.
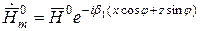Граничные условия: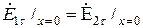 
.
Падающая волна частично (или полностью) отражается от границы и частично (или полностью) проходит во вторую среду. Можно считать, что ориентация векторов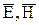 
относительно направления распространения не меняется.
Для отраженной волны:
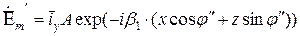
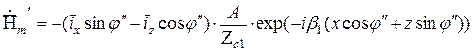
при этом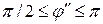 
и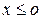 
.
Для преломленной волны:
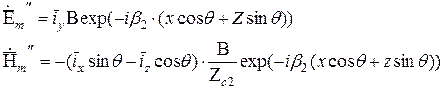
при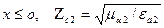 
.
Граничные условия должны выполняться при любых Z. Это возможно только, если зависимость от Z для всех трех векторов одинакова:
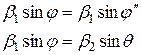
так как:
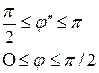
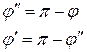
и угол падения равен углу отражения:
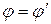(2.23)
Из другого равенства:
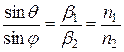(2.24)
n - показатель преломления среды:
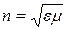
Определим постоянные А и В на границе раздела (А и В амплитуды отражённой и преломлённой волн соответственно ):
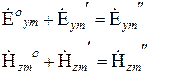
При Х = 0:
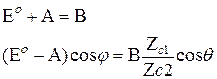
A и B пропорциональны E°: А = RЕ°, В = ТЕ°.
R - коэффициент отражения, T - коэффициент преломления (коэффициенты Френеля).
В случае нормальной поляризации:
1+R^=T^;
1-R^=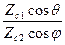 
Т^
Модуль R характеризует соотношение между амплитудами падающей и отражённой волны, а аргумент - сдвиг фаз между этими полями:
R^ =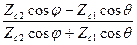 
T^ =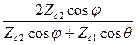 
вывод при параллельной поляризации аналогичен - самостоятельно.
R| |=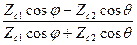 
T|| =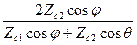 
Остановимся на простейших следствиях, вытекающих из этих соотношений.
Для нормального падения ЭМВ имеем j = 0 и формулы для R и T переходят в:
R^= - R||=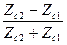 
; T^= T|| = 
.
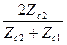При нормальном падении плоскость падения становится неопределённой и различие поляризаций пропадает.
Знак ’’минус’’ за счёт того, что R^ и T^ коэффициенты по электрическому полю, Rêê и Têê - по магнитному.
Угол Брюстера
В связи со сказанным, возникает вопрос о том, какими свойствами должно обладать вещество, чтобы являться ’’оптической невидимкой’’.
Так как визуальное обнаружение любого тела обусловлено волнами, отражёнными и рассеянными телом под самыми различными углами, то для этого необходимо, чтобы R^ и Rêê равнялись 0 для любого угла падения j, что для реального диэлектрика означает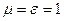 
.
Т.е. электромагнитные свойства вещества неотличимы от свойств вакуума, если он – первая среда, или (m/e = 1): ZС2 = ZС1.
Если условие ZС1 = ZС2 не выполняется, то из условия следует:
1) для параллельной поляризации: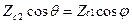 
, возводим в квадрат обе части равенства и учтём второй закон Снеллиуса в следующей форме:
.
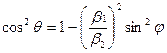Для обычных диэлектриков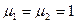 
, после преобразований:
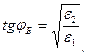
где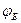 
– 
угол Брюстера
Для обычных диэлектриков существует угол падения, при котором падающая волна целиком проходит во вторую среду.
2) случае нормальной поляризации при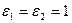 
;
