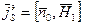Граничные условия для векторов ЭМП
1. Нормальные составляющие
Соотношения, показывающие связь между значениями векторов ЭМП в разных средах, у поверхности раздела называют граничными условиями. (Используют интегральную запись уравнений Максвелла). На поверхности раздела двух сред с параметрами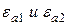 
соответственно, выделим малый элемент 
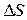так чтобы:
1. его можно считать плоским;
2. распределение Dn в пределах 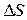должно быть равномерным.
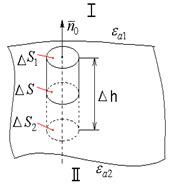
Построим на 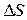цилиндр с основаниями в разных средах. Используем третье уравнение Максвелла:
.
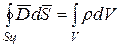Поверхность цилиндра:
.
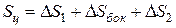Устремим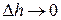 
так, чтобы 
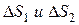оставались в разных средах:
;
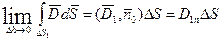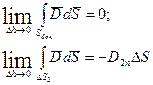
Если заряд не сосредоточен на поверхности раздела, то:
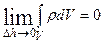
и нормальная компонента вектора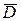 
непрерывна при переходе из одной среды в другую. Если заряд распределен по поверхности раздела в виде бесконечно тонкого слоя с поверхностной плотностью:
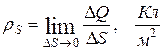
тогда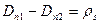 
, то есть нормальная компонента вектора D претерпевает скачек на величину 
поверхностного заряда. Для вектора Е:
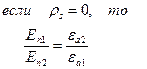
Нормальная компонента Е претерпевает разрыв. На самом деле поверхностных зарядов не бывает, толщина слоя конечна и D меняется постепенно. Но математическая модель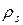 
удобнее.
Тангесальные составляющие
Из произвольной точки на поверхности S раздела двух изотропных сред проведем единичную нормаль n0. Через нее проведем плоскость Р и на линии пересечения Р и S выделим малый отрезок D l такой, чтобы считать его прямолинейным и `E неизменной в его пределах.
На отрезке Dl построим контур ABCD высотой Dh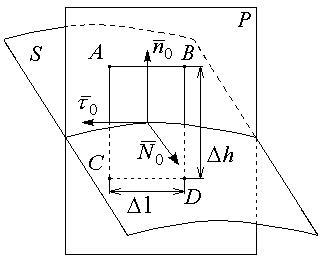 
` 
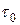- касательная к D l,
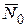- нормаль к P, образующий правовинтовую систему с ABCD и 
.
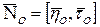Используем второе уравнение Максвелла:
,
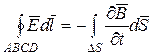где
.
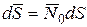Левую часть представим в виде суммы четырех интегралов:
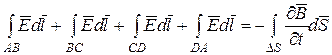
и оставляя AB и CD в разных средах, устремляем Dh ® 0:
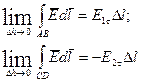
Так как Е и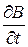 
конечные величины, то:
.
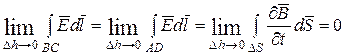А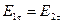 
, то есть касательная, составляющая вектора Е, непрерывна при переходе через границу раздела двух сред.
Полная система граничных условий:
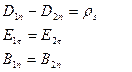
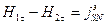
где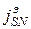 
- плотность поверхностного тока, направленного ортогонально вектору 
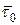(или его составляющая).
На поверхности раздела с идеальным проводником 
, внутри которого поле отсутствует, согласно уравнению Максвелла будут справедливы следующие граничные условия:
,
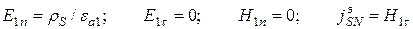или для Н в векторной форме:
