Плоской называют волну, распространяющуюся вдоль какой либо координаты и неизменную в каждый фиксированный момент времени в плоскости перпендикулярной этой координате .
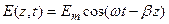
Параметр b играет роль «пространственной» частоты процесса – коэффициент фазы (1/м).
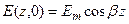
E(z,0) – периодична ; ее период: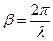 
, где l - длина волны.
Поверхность, удовлетворяющая условию: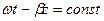 
называется волновой фронт (фазовый фронт, поверхность равных фаз), перемещающийся вдоль оси Z с фазовой скоростью:
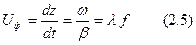
Величину a называют коэффициентом ослабления плоской волны в среде (1/м).
В расчетах чаще используют погонное затухание:
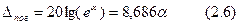дБ/м
g - коэффициент распространения.
Воспользуемся вторым уравнением Максвелла:
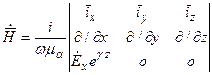
и найдем Н:
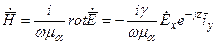
подставляем величину g:
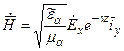
Некоторые выводы :
- в однородной плоской волне векторы Е и Н перпендикулярны;
- и Е и Н перпендикулярны оси распространения – поперечная волна;
- комплексные амплитуды векторов Е и Н в любой точке пространства связаны коэффициентом пропорциональности Zc;
Zc - характеристическое (волновое) сопротивление
; 
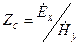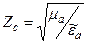(2.7)
Zc характеризует среду и, в общем случае, не связан с тепловыми потерями.
Определим плотность потока мощности плоской ЭМВ:
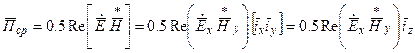
или с учетом Zс:
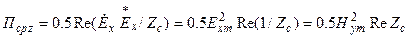(2.8)
Рассмотрим, как изменятся приведенные выше соотношения, если среда распространения – вакуум: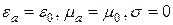 
.
Коэффициент распространения: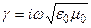 
чисто мнимый (потерь нет).
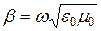тогда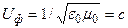 
и не зависит от частоты.
Так как Zо – действительное, то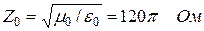 
, значит Е и Н колеблются в фазе. Отметим, что для атмосферного воздуха это тоже справедливо.
В среде без потерь, но с e>1, m>1:
;
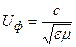(2.9)
На практике в СВЧ - диапазоне используют, как правило, диэлектрик с малыми потерями и m » 1 . Для расчета основных характеристик плоских ЭМВ используются следующие выражения:
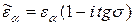
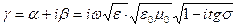
Так как tgs<<1 можно использовать приближенную формулу:
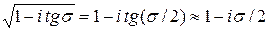
и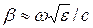 
То есть, в случае малых потерь, b - практически не изменился,
a- прямо пропорционален w и s:
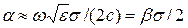(2.10)
Для сопротивления (использовали 1/(1-Х) » 1 + Х при |Х|<<1):
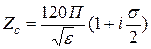
(2.11)
Так как Zс - комплексная величина, то Е и Н колеблются не синфазно и угол сдвига фаз приблизительно равен s/2.
В хорошо проводящих средах, даже при постоянстве mа, абсолютная диэлектрическая проницаемость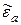 
является функцией частоты: 
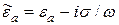, то есть наблюдается частотная дисперсия.
Говорят, что на заданной частоте w материальная среда является хорошо проводящей (металлоподобной), если:
s ¤ w >> e а (2.12)
То есть плотность токов проводимости значительно превышает плотность токов смещения и поляризационных токов.
Как следствие на низких частотах неидеальные диэлектрики и полупроводники становятся металлоподобными (сухая почва при частоте f = 1 МГц ведет себя как хорошо проводящая среда).
Но даже на самых высоких частотах радиодиапазона неравенство (2.12) выполняется для металлов с большим запасом.
В хорошо проводящей среде можно приближенно считать: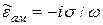 
.
Тогда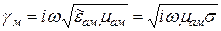 
; 
.
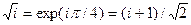Перейдем к a и b:
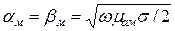(2.13)
обе величины сильно зависят от w, дисперсия ярко выражена:
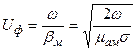
и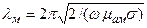 
,
а характеристическое сопротивление:
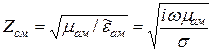(2.14)
Величина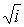 
означает, что в проводнике вектор Н сдвинут по фазе относительно вектора Е на 45°.
Если a ¹ 0, то амплитуда плоской ЭМВ изменяется вдоль координаты распространения Z по закону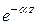 
.
Расстояние, на котором амплитуда уменьшается в е раз, называют глубиной проникновения или толщиной поверхностного слоя (d):
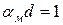
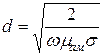(2.15)
На СВЧ диапазоне глубина проникновения очень мала. Для меди на 10 ГГц d = 0,6 мкм, это позволяет использовать тонкие (10-20 мкм) слои хороших проводников для уменьшения потерь.
Поляризация волн
Полагаем, что вектор Е имеет две составляющие,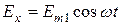 
и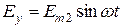 
. Найдем положение кривой, которая служит геометрическим местом концов вектора Е суммарного процесса.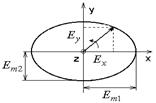 
Перепишем:
,
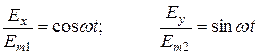возводим их в квадрат и складываем:
,
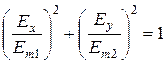это уравнение эллипса, а про волну говорят, что это эллиптически поляризованная волна.
В этом случае вектор Е вращается против часовой стрелки, если смотреть с конца iz – лево поляризованная волна.
Частные случаи:
Равна нулю одна из составляющих или сдвиг фаз между ними равен нулю. Тогда конец вектора Е перемещается вдоль линии произвольно, в общем случае, ориентированной относительно системы координат. Волна – линейно поляризованная.
Равны амплитуды Еm1 = Еm2, а сдвиг фаз - 90°. Тогда кривая окружность, волну называют волной с круговой поляризацией.
Легко заметить, что суперпозиция двух волн с линейными поляризациями, сдвинутых по фазе и пространственно на 90°, дают эллиптически поляризованную волну, две волны с круговыми поляризациями и противоположными направлениями вращения в результате суперпозиции дают волну линейно поляризованную.