Такие волны называются плоско (или линейно) поляризованными волнами.
Плоскость, в которой происходит колебание вектора Е называют плоскостью поляризации линейно поляризованной волны, а плоскость колебаний вектора Н – плоскостью колебаний. Ранее эти названия были обратными (см. [1]).
6. Все сказанное о стоячих волнах в упругих средах относится и к электромагнитным волнам. В этом случае, однако, волна характеризуется не одним вектором, а двумя взаимно перпендикулярными векторами Е и Н.
Стоячая электромагнитная волна состоит из двух стоячих волн - магнитной и электрической, колебания которых сдвинуты по фазе на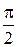 
.
7. Энергия электромагнитных волн.
Объемная плотность энергии электромагнитного поля в линейной изотропной среде задается соотношением:
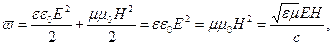
с - скорость света в вакууме.
В случае плоской линейно поляризованной монохроматической волны, распространяющейся вдоль положительного направления ОY, напряженность электрического поля задается уравнением:
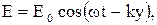
соответственно объемная плотность энергии этой волны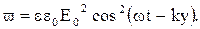 
Значение объемной плотности энергии волны меняется за период от 0 до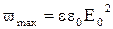 
.Среднее за период значение энергии равно:
.
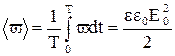8. Вектор плотности потока энергии электромагнитной волны называется вектором Умова - Пойнтинга:
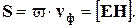
Для линейно поляризованной монохроматической волны вектор Пойнтинга направлен в сторону распространения волны и численно равен: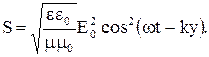 
Интенсивность электромагнитной волны равна модулю среднего значения вектора Пойнтинга за период его полного колебания:
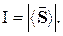
Интенсивностью электромагнитной волны называется физическая величина, численно равная энергии, переносимая волной за единицу времени через единицу площади поверхности, расположенной перпендикулярно к направлению распространения волны.
Интенсивность бегущей монохроматической волны: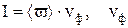 
- фазовая скорость волны, 
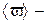среднее значение объемной плотности энергии поля волны.
Интенсивность света (электромагнитных волн, рассматриваемых в оптике) прямо пропорциональна квадрату амплитуды колебаний вектора напряженности Е поля световой волны.
Плоские электромагнитные волны
Рассмотрим бесконечное трехмерное пространство с заданными электродинамическими параметрами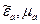 
, одинаковыми во всех точках. Кроме того, полагаем, что свободные заряды отсутствуют r = 0. Гармонически изменяющийся электромагнитный процесс будет описываться системой уравнений Максвелла:
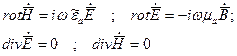
Возьмем rot от второго уравнения и подставим в него первое уравнение:
.
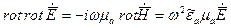Используем векторное тождество:
.
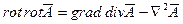И так как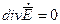 
, то: 
.
Получаем: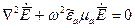 
(2.1)
Это уравнение называют уравнением Гельмгольца.
Введем параметр: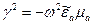 
(2.2)
и уравнение (2.1) перепишется: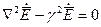 
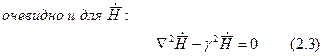
Система (2.3) – система однородных дифференциальных уравнений второго порядка. Решение этой системы в общем виде достаточно громоздкое. Для простоты положим:
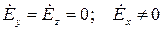
кроме того,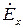 
зависит только от координаты Z, то есть:
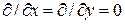
тогда первое уравнение системы (2.3) из трех уравнений начинает описываться только одним:
.
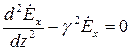Общее решение этого линейного уравнения:
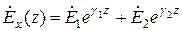
Где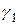 
и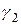 
корни уравнения (2.2). Распишем его:
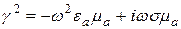
В комплексной плоскости:
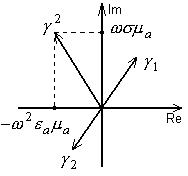
В дальнейшем будем пользоваться только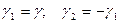 
.
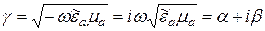
и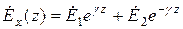 
Подобные процессы давно известны – однородная плоская волна. Первое слагаемое – волна, распространяющаяся в сторону уменьшения Z. Второе – в сторону увеличения.