Длиной волны называется наименьшее расстояние между двумя точками среды, совершающими колебания в фазе (т.е. разность их фаз равна ).
Если точки разделены расстоянием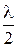 
, их колебания происходят в противофазе.
2. Фазовая скорость волны.
Из повседневного опыта известно, что бегущие по воде волны распространяются с постоянной скоростью, пока свойства среды, например, глубина воды, не меняется, что говорит о том, что скорость распространения волнового процесса в пространстве остается постоянной. В случае гармонических бегущих волн (см. определение выше) эта скорость называется фазовой.
Фазовая скорость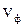 
- это скорость распространения данной фазы колебаний, т.е. скорость волны.
Связь длины волны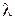 
, фазовой скорости 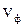и периода колебаний Т задается соотношением:
.
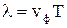Учитывая, что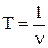 
, где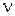 
- линейная частота волны, 
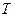- период, а циклическая частота волны 
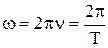, получим разные формулы для фазовой скорости:
.
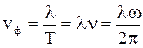Для волнового процесса характерна периодичность по времени и по пространству.
Т – период колебаний точек среды. Роль пространственного периода играет длина волны 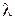. Соотношение между периодом и циклической частотой задается формулой: 
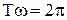. Аналогичное соотношение можно записать для длины волны и величиной k, называемой волновым числом: 
.
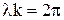4. Фронт волны. Волновая поверхность.
При прохождении волны по среде ее точки вовлекаются в колебательный процесс последовательно друг за другом.
Геометрическое место точек, до которого к некоторому моменту времени дошел колебательный процесс, называется волновым фронтом.
Геометрическое место точек, колеблющихся в фазе, называется волновой поверхностью.
Волновой фронт – частный случай волновой поверхности. Волновой фронт все время перемещается. Волновые поверхности остаются неподвижными. Они проходят через положения равновесия частиц среды, которые колеблются в одинаковой фазе.
При описании распространения волн широко используют понятие луча. Направления, в которых распространяются колебания, называются лучами. В изотропной среде (см. определение выше) лучи перпендикулярны волновым поверхностям (фронту) и имеют вид прямых линий. В анизотропной среде, а также при дифракции волн, лучи могут искривляться.
Форма волнового фронта определяет вид волны: сферические (от точечного источника в изотропной среде), эллиптические (в анизотропной среде), цилиндрические (от протяженных источников), плоские и другие. На достаточно большом расстоянии от источника небольшой участок любого фронта можно считать плоским.
Если известно положение фронта волны в некоторый момент времени и скорость волны 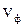, то его положение в последующий момент времени можно определить на основе принципа Гюйгенса. Согласно этому принципу все точки поверхности волнового фронта являются источниками вторичных волн. Искомое положение волнового фронта совпадает с поверхностью, огибающей фронты вторичных волн.
5. Уравнение бегущей волны.
Уравнением упругой волны называется зависимость от координат и времени скалярных или векторных величин, характеризующих колебания среды при прохождении по ней волны.
Упругая волна называется синусоидальной или гармонической, если соответствующие ей колебания частиц среды являются гармоническими. Так, рассмотренные выше бегущая и отраженная волны являются гармоническими волнами.