W - полный запас энергии ЭМП внутри объема V в фиксированный момент времени
Общие положения теории ЭМП
Основные законы электродинамики
В курсе «Теория передачи электромагнитных волн» рассматривается классическая нерелятивистская электродинамика. Это частная версия теории электромагнетизма, которая отличается, прежде всего, тем, что ее основные понятия - напряженности полей, заряды и токи - не выводятся из чего-либо, а постулируются.
Кроме того, методы, которые мы будем использовать, справедливы в условиях, когда скорости движущихся тел много меньше скорости света.
Согласно основным положениям макроскопической ЭД ЭМП в каждой точке в каждый момент времени определяется четырьмя величинами: 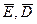 - характеризующими электрическое поле, и
- характеризующими электрическое поле, и 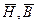 - магнитное поле. Кроме этих четырех векторов в уравнениях электромагнитного поля присутствуют еще две величины: плотность заряда
- магнитное поле. Кроме этих четырех векторов в уравнениях электромагнитного поля присутствуют еще две величины: плотность заряда 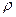 и плотность тока
и плотность тока 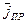 , они характеризуют источники поля - заряды и токи. (В макроскопической ЭД r – плотность свободного электрического заряда, а j - плотность электрического тока (тока проводимости)).
, они характеризуют источники поля - заряды и токи. (В макроскопической ЭД r – плотность свободного электрического заряда, а j - плотность электрического тока (тока проводимости)).
Если нет макроскопических перемещений вещества, то плотность тока и плотность заряда связаны уравнением непрерывности:
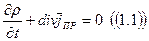 (1.1)
(1.1)
Выражающим тот факт, что ток проводимости обусловлен движением свободных зарядов. 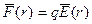 - сила действующая на заряд q. Векторное поле
- сила действующая на заряд q. Векторное поле 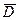 необходимо для описания электрического поля в материальной среде (например, в диэлектрике) - поле электрического смещения.
необходимо для описания электрического поля в материальной среде (например, в диэлектрике) - поле электрического смещения.
Сила Лоренца: 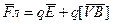 ,
,
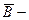 поле магнитной индукции.
поле магнитной индукции.
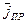 - характеризует силу тока через единичную площадку перпендикулярную вектору скорости заряженных частиц.
- характеризует силу тока через единичную площадку перпендикулярную вектору скорости заряженных частиц.
q - объемная плотность заряда в объеме V.
Векторы ЭМП и величины j и r зависят от 3-х пространственных координат и времени t. Они связаны между собой системой уравнений Максвелла:
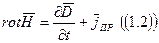 , (1.2)
, (1.2)
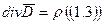 , (1.3)
, (1.3)
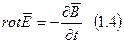 , (1.4)
, (1.4)
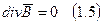 . (1.5)
. (1.5)
При этом здесь и далее мы будем использовать систему единиц СИ.
Размерности величин в этой системе: 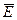 В/м,
В/м, 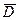 Кл/м2,
Кл/м2, 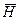 А/м,
А/м, 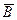 Тл,
Тл, 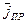 А/м2,
А/м2, 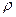 Кл/м3.
Кл/м3.
Уравнение (1.2) называют обычно первым, а (1.4) - вторым уравнениями Максвелла Дж. Кларка. (1873 - трактат об электричестве и магнетизме).
Все 4 уравнения - обобщение опытных данных.
Уравнение (1.2) - дифференциальная формулировка закона полного тока и гипотезы Максвелла о токе смещения.
Уравнение (1.3) - закон Гаусса.
(1.4) - закон электромагнитной индукции (Фарадей).
(1.5) - закон неразрывности магнитных силовых линий.
Система уравнений 1.2-1.5 справедлива для электромагнитных полей в любых средах, но их недостаточно для решения конкретных задач (неизвестных больше чем уравнений).
(1.3) и (1.5) - практически скалярные уравнения.
В систему следует включить уравнения, учитывающие влияние среды на протекающие в ней электромагнитные явления.
Материальные уравнения
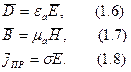
Величиной 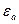 - абсолютной диэлектрической проницаемостью - характеризуют свойства диэлектриков (веществ не проводящих электрический ток) неполярных и полярных:
- абсолютной диэлектрической проницаемостью - характеризуют свойства диэлектриков (веществ не проводящих электрический ток) неполярных и полярных:
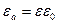
Электрическая постоянная:
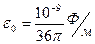
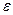 - относительная диэлектрическая проницаемость (безразмерная)
- относительная диэлектрическая проницаемость (безразмерная)
(вакуум, воздух 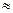 1; полиэтилен = 2,25; пресная вода
1; полиэтилен = 2,25; пресная вода 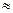 81).
81).
Свойства магнетиков характеризуют магнитная проницаемость или магнитная проницаемость:
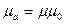 .
.
Размерная константа, называемая магнитной постоянной:
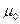 =4
=4 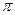 *10-7
*10-7 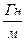
Величина 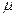 может быть меньше 1 и много больше.
может быть меньше 1 и много больше.
У диамагнетиков - уменьшающих поле - 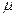 <1 (как правило, близко к единице). К ним относится большинство веществ.
<1 (как правило, близко к единице). К ним относится большинство веществ.
У парамагнетиков, увеличивающих магнитное поле, - 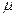 незначительно больше 1. (кислоты, азот некоторые металлы и т.д.)
незначительно больше 1. (кислоты, азот некоторые металлы и т.д.)
Особый класс веществ - ферромагнетики. У них 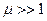 .
.
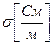 - удельная проводимость. У серебра 6.1*107; у меди 5.7*107 и т.д.
- удельная проводимость. У серебра 6.1*107; у меди 5.7*107 и т.д.
Уравнение (1.8) называют законом Ома в дифференциальной форме.
Уравнения 1.6-1.8 охватывают электромагнитные свойства достаточно большого числа сред, но многие свойства реальных веществ не учитывают.
Имеется в виду тот факт, что соотношения прямой пропорциональности между E и D , B и H - линейные среды могут нарушать.
В диэлектрике нелинейная зависимость 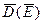 наблюдается каждый раз, когда E становится очень высокой и возникает электрический пробой.
наблюдается каждый раз, когда E становится очень высокой и возникает электрический пробой.
Согласно макроскопической теории поля электромагнитная энергия распределена в пространстве, занятом полем, с некоторой объемной плотностью таким образом, что электромагнитная энергия, содержащаяся в объеме V, выражается в виде объемного интеграла:
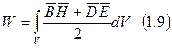 (1.9)
(1.9)
W - полный запас энергии ЭМП внутри объема V в фиксированный момент времени
(измеряется в Дж).
Изменяться во времени эта энергия может за счет двух процессов:
1. Она может внутри данного объема превращаться другие, неэлектромагнитные формы энергии (тепловая, химическая, кинетическая ускоренных частиц...) или возникать из неэлектромагнитных форм.
2. Эта энергия, оставаясь электромагнитной, может вытекать из данного объема (или втекать в него) через поверхность S, ограничивающую данный объем.
Первый процесс характеризуется мощностью потерь РПОТ.
Второй - мощностью излучения S.
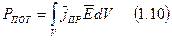 ,
,
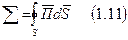 ,
,
где
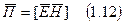
вектор плотности потока мощности электромагнитного поля - вектор Пойнтинга (1884 - английский ученый)
Величины РПОТ и S могут быть положительными и отрицательными (отрицательность РПОТ - идет превращение других видов энергии в электромагнитную; отрицательность S показывает, что в данный объем поступает энергия из внешнего пространства).
Выражения (1.11)-(1.12) справедливы для любых сред.
Три энергетические величины РПОТ, W и S связаны между собой соотношением Умова-Пойнтинга:
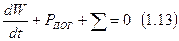 ,
,
которое представляет собой математическую формулировку закона сохранения энергии для электромагнитного поля.
Так же как интегральная величина 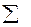 связана с дифференциальной П, величина объемной плотности электромагнитной энергии связана с W:
связана с дифференциальной П, величина объемной плотности электромагнитной энергии связана с W:
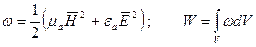
и объемная плотность мощности тепловых потерь:
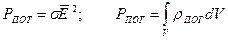
Тогда уравнение (1.13) будет выглядеть следующим образом:
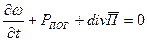 (1.14)
(1.14)
Теорема Остроградского-Гаусса
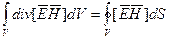
Мы уже говорили, что токи и заряды являются источниками ЭМП, а также сами возникают под действием поля.
На практике приходится учитывать также токи и заряды, которые вызываются внешними источниками и практически не зависят от возбужденного ими ЭМП.
Такие токи принято называть "сторонними" и векторное поле плотности сторонних токов 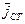 следует ввести, как заранее заданную функцию в уравнения Максвелла, а также в уравнение Умова-Пойнтинга:
следует ввести, как заранее заданную функцию в уравнения Максвелла, а также в уравнение Умова-Пойнтинга:
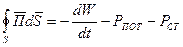 ,
,
где 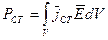 .
.
Сводка уравнений Максвелла:

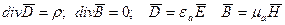
* Уравнения в интегральной форме записать самостоятельно.
Это система дифференциальных уравнений в частных производных первого порядка относительно шести неизвестных функций (ЕХ ЕУ ЕZ НХ НУ НZ), которые зависят от трех пространственных координат и от времени t.
Так как в большинстве практических задач материальные среды можно считать линейными, то в них будет справедлив принцип суперпозиций ЭМП:
Если 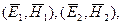 частные решения УМ, то решением будет и сумма вида: (
частные решения УМ, то решением будет и сумма вида: ( 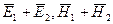 ).
).
Решение уравнений можно значительно упростить, если исключить временную переменную.
Любой сигнал может быть разложен на спектр гармонических составляющих по преобразованию Фурье.
Для гармонически изменяющего в некоторой заданной точке пространства вектора (например, E):
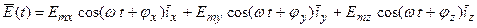
Emx, Еmy, Emz - амплитуды отдельных составляющих поля 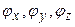 - соответствующие начальные фазы, по-другому это выражение можно записать:
- соответствующие начальные фазы, по-другому это выражение можно записать:
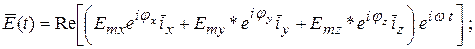
Вектор 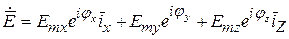 принято называть комплексной амплитудой поля E в заданной точке пространства (считается, что частота поля w - известна).
принято называть комплексной амплитудой поля E в заданной точке пространства (считается, что частота поля w - известна).
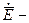 пространственные, в общем случае, трехмерные векторы (изобразить вспомогательным вектором, вращающимся в комплексной плоскости нельзя).
пространственные, в общем случае, трехмерные векторы (изобразить вспомогательным вектором, вращающимся в комплексной плоскости нельзя).
Exp – эти множители характеризуют только фазы, т.е.
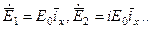
Не образуют угол 900, а параллельны орту ix и сдвинуты по фазе на 900.
Связь между E(t) и 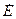 :
:
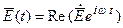
Если подставить подобные выражения для всех векторов в уравнения Максвелла и сократить общий множитель, то получим:
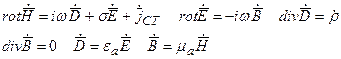
Если объединить первое уравнение и пятое, то получим:
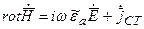
где
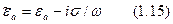
комплексная диэлектрическая проницаемость данного вещества, учитывающая и проводящая и поляризационные свойства.
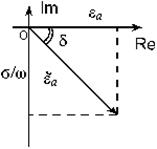 |
Действительная часть - интенсивность процесса поляризации, мнимая - плотность токов проводимости (потери).
В комплексной плоскости
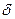 - угол диэлектрических потерь (в справочниках обычно приводят tg
- угол диэлектрических потерь (в справочниках обычно приводят tg 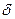 ) :
) :
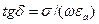
На частотах СВЧ диапазона для хороших диэлектриков tg 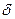 =10-5¸10-4, если tg
=10-5¸10-4, если tg 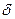 >10-3 - диэлектрик принято считать плохим.
>10-3 - диэлектрик принято считать плохим.
Выразим через комплексные амплитуды вектор Пойнтинга.
Воспользуемся соотношениями:
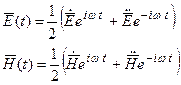
подставляем их в…
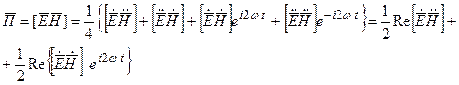
Первое слагаемое неизвестно во времени, а второе меняется с удвоенной частотой - колеблющаяся составляющая вектора Пойнтинга, среднее за период значение которой равно 0; 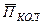 .
.
Первое слагаемое практически равно плотности потока мощности усредненной за период (действительный вектор):
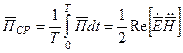
При анализе гармонических полей удобней использовать комплексный вектор Пойнтинга:
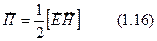 и
и
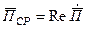
Комплексный вектор Пойнтинга аналогичен комплексной мощности гармонического колебания.
Если он чисто мнимый, то процесс не переносит мощности (перенос реактивной мощности).
Принцип перестановочной двойственности
Рассмотрим две системы:
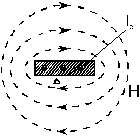
1. Пластинка (вид с торца) с электрическим током IЭ.
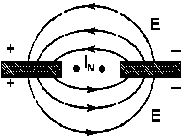
2. Две заряженные полуплоскости.
 |  | ||
Ширина пластинки и зазора - 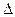 .
.
Картинки однотипны с точностью до направлений стрелок.
Это сходство позволяет формально предположить: в щели параллельно кромкам протекает гипотетический ток IM , называемый магнитным током (физически не существует).
Геометрическое сходство полей - следствие симметрии двух основных уравнений Максвелла:
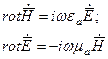
Которые переходят одно в другое при перестановках 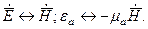
Если в первом уравнении был ток jCT Э, то следует предположить наличие jCT M и 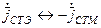 .
.
Если найдено решение какой-либо задачи ЭД, то простая перестановка дает решение дуальной (двойственной) задачи, причем физически реализуемой.
Лемма Лоренца
Оценим связь между полями, возбужденными двумя независимыми системами сторонних токов.
Поле, созданное одной системой:
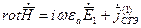 ;
; 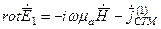 (1.17)
(1.17)
для другой
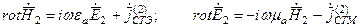 (1.18)
(1.18)
Проделаем ряд операций:
- умножим скалярно первое уравнение из (1.17) на вектор 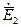
- умножим скалярно второе уравнение из (1.18) на вектор 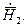
- вычтем второе равенство из первого, учитывая векторное тождество:
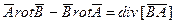
получим:
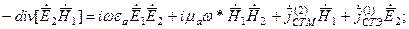 ( ** )
( ** )
Теперь умножим второе уравнение из (1.17) на 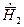 , а первое из (1.18) на
, а первое из (1.18) на 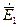 и вычтем второе равенство из первого, получим:
и вычтем второе равенство из первого, получим:
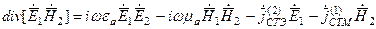 ( *** )
( *** )
Складываем почленно равенства (**) и (***), получим:
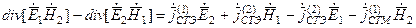 (1.19)
(1.19)
Уравнение (1.19) - Лемма Лоренца в дифференциальной форме.
Векторные произведения [E1H2] и [E2H1] в левой части уравнения - взаимные векторы Пойнтинга двух независимых процессов.
Проинтегрируем уравнение (1.19) по произвольному объему V и используем теорему Остроградского-Гаусса, получаем Лемму Лоренца в наиболее общем виде:
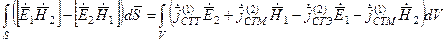
где S - поверхность, ограничивающая объем V.
Предположим, что V - все пространство, т.е.(S - бесконечно большая).
Полагаем, что источники сосредоточены в конечной области пространства и, кроме того, на бесконечности поля убывают быстрее, чем 1/R, где R - расстояние от фиксированной точки. (Это физически обоснованно, т.к. в пространстве всегда будут причины для ослабления поля - потери)
Интеграл в левой части при этом становится исчезающе малым, и Лемма Лоренца для безграничного пространства, имеющего в каждой точке некоторые потери, принимает вид:
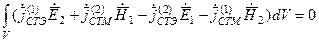 .
.
Упростим задачу, полагая, что в пространстве есть только сторонние электрические токи (любая проволочная антенна), тогда:
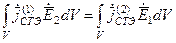
Последнее соотношение - теорема взаимности для антенн, возбуждаемых электрическими токами.
В простейшем случае если имеются две идентичные антенны, возбуждаемые одинаковым образом, то первая антенна будет создавать вблизи второй такое же поле, как вторая вблизи первой, независимо от параметров среды, разделяющей их (исключение – анизотропные среды).
В общем случае теорема взаимности связывает свойства приемной антенны со свойствами ее в режиме передачи.
В частности Диаграммы Направленности, (в дальнейшем ДН) в обоих режимах совпадают.
В анизотропных средах теорема взаимности справедлива, если:
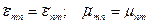
(для ферритов - нет, для кристаллов - да).
ВОЛНЫ.
Процесс распространения колебаний в пространстве называется волной.
Волны, образованные внешним воздействием, приложенным к упругой среде, называются бегущими волнами: они «бегут» от создающего их источника. Важное свойство бегущих волн заключается в том, что они переносят энергию и импульс. Если внешняя сила совершает гармонические колебания, то вызванные ею волны называются гармоническими бегущими волнами.
Волновой процесс обусловлен наличием связей между отдельными частями системы, в зависимости от которых, мы имеем упругую волну той или иной природы.








