Шифратор призначений для перетворення цифрової інформації, що подана унітарним n-розрядним кодом, у еквівалентний двійковий m‑розрядний код.
Унітарний код це код для якого може існувати тільки один активний стан змінної Xi із множини вхідних сигналів {Xn-1…X1,X0}. Отже, шифратор - це перетворювач унітарного коду "1 з n" у двійковий паралельний код, у якого число виходів m однозначно зв’язане з числом входів n як 2m. Якщо n=2m , що означає використання повного набору вихідних двійкових комбінацій Yi, такий шифратор називають повним. Наприклад, шифратор 8-3 є повним, бо він реалізує повний набір можливих комбінацій змінних Xi (n=8) у повний вихідний набір Yi (m=2) як 23=8.
У неповному шифраторі число входів m не відповідає числу всіх можливих вихідних комбінацій 2m, причому завжди n<2m, що відповідно утворює певне число невикористаних вихідних наборів. Прикладом неповного шифраторa, який найчастіше зустрічається на практиці, є шифратор 10-4, що використовується для кодування десяткових чисел у двійково-десятковий код ДДК /8-4-2-1/, Такий шифратор можна застосовувати для кодування десяткових символів (0...9), наприклад, з клавіатури пульта керування. Схематичне позначення шифратора наведене на рис.3.1а, а схема внутрішньої будови на рис.3.1б. Здійснити синтез повного або неповного шифратора можна на базі ЛЕ. Як приклад, здійснимо синтез повного шифратора 8-1.
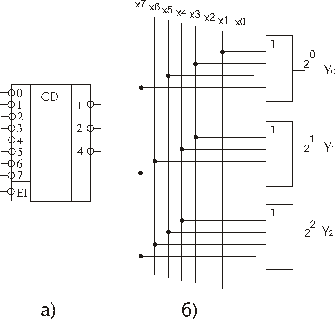
Рис. 3.1 Умовне позначення та внутрішня будова шифратора 8-3
Такий шифратор може бути описаний наступною системою логічних функцій:
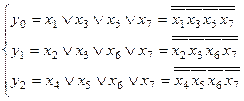 ( 3.1)
( 3.1)
або таблицею істинності:
Таблиця 3.1 Таблиця істинності шифратора 8-3
| n | x0 | x1 | x2 | x3 | x4 | x5 | x6 | x7 | Y2 | Y1 | Y0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 4 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
Окремі ІС практично зустрічаються рідко, як правило існують мікросхеми, що виконують комбіновані функції, наприклад "шифратор/дешифратор". Крім того, практично використовують шифратори, у яких вихідний код завжди має найбільший номер активного вхідного сигналу {X0..Xn} – так звані пріорітетні шифратори. Приклад роботи пріорітетного шифратора: Вхід{x0=1,x1=1,x2=0, x3=0, ,x4=1}, тоді вихід Y=4.
Дешифратор призначений для розпізнавання (дешифрацій) числа, яке подане позиційним 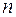 -розрядним двійковим кодом. Найчастіше дешифратор
-розрядним двійковим кодом. Найчастіше дешифратор 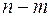 виконує функцію перетворення двійкового кода в унітарний код "1 з
виконує функцію перетворення двійкового кода в унітарний код "1 з 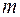 ", тобто виконує функцію, що обернена дії шифратора, і тому для повного дешифратора справедливе співвідношення
", тобто виконує функцію, що обернена дії шифратора, і тому для повного дешифратора справедливе співвідношення 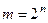 де
де 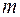 - порядковий номер виходу
- порядковий номер виходу 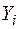 дешифратора. Аналітичний опис дешифратора розглянемо на прикладі повного дешифратора 3-8, який описується системою логічних функцій:
дешифратора. Аналітичний опис дешифратора розглянемо на прикладі повного дешифратора 3-8, який описується системою логічних функцій:
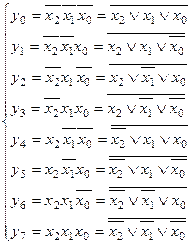 ( 3.2 )
( 3.2 )
Такому опису відповідає схематичне представлення дешифратора на рис. 3.2 а, та його внутрішня будова (рис.3.2.б).

Рис. 3.2 Схематичне позначення та внутрішня структура дешифратора 3-8
У неповного дешифратора число виходів 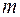 не відповідає значенню
не відповідає значенню 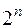 , причому
, причому 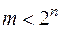 . В інтегральному виконанні зустрічаються як повні (К155ИД3, К155ИД7), так і неповні (К555ИД5, К555ИД10, К561ИД1), а також здвоєні (К155ИД4) дешифратори.
. В інтегральному виконанні зустрічаються як повні (К155ИД3, К155ИД7), так і неповні (К555ИД5, К555ИД10, К561ИД1), а також здвоєні (К155ИД4) дешифратори.
У випадках, коли потрібно побудувати дешифратор на велику кількість виходів на базі дешифраторів з меншим числом виходів, застосовують принцип каскадування. Він полягає у тому, що дані входи дешифраторів розбивають довільним чином на групи, кожна з яких реалізує свою групу логічних функцій. При цьому всі дешифратори повинні бути керованими, тобто мати дозволяючі входи EІ. На рис. 3.3 показано двокаскадне з’єднання двох дешифраторів 3-8 для побудови повного дешифратора 4-16, що має входи дозволу 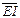 . Каскад 1 працює при активних входах
. Каскад 1 працює при активних входах 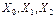 за умови
за умови 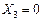 . Як тільки на входах дешифратора з'явиться код {
. Як тільки на входах дешифратора з'явиться код { 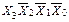 }={1000}, верхній каскад закриється, оскільки
}={1000}, верхній каскад закриється, оскільки 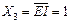 , а відкриється нижній каскад, який через інвертор отримує дозволяючий рівень
, а відкриється нижній каскад, який через інвертор отримує дозволяючий рівень 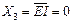 .
.
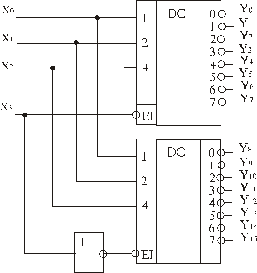
Рис. 3.3 Каскадний синтез дешифратора 4-16
3.2 Мультиплексори та демультиплексори
Це КП, що призначені для комутації цифрових каналів під дією двійкового коду керуючих сигналів.
Мультиплексор (Multiplexor: MUX) призначений для передачі (комутації) сигналів від одного з кількох інформаційних входів Xi (шини даних) на один вихід. Крім інформаційних входів мультиплексор має адресні входи 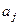 , двійковий код на яких визначає номер активного інформаційного входу, який треба під'єднати до виходу схеми. Отже, мультиплексор має
, двійковий код на яких визначає номер активного інформаційного входу, який треба під'єднати до виходу схеми. Отже, мультиплексор має 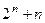 входів і один вихід (
входів і один вихід (  -число інформаційних входів; n-число адресних входів). Керований мультиплексор має ще один вхід дозволу мультиплексування E.
-число інформаційних входів; n-число адресних входів). Керований мультиплексор має ще один вхід дозволу мультиплексування E.
Для побудови мультиплексора 2n®1 потрібно мати багатовходовий ЛЕ типу І-АБО, що забезпечує передачу з інформаційної шини даних одного з 2n сигналів, а для керування комутацією - дешифратор.
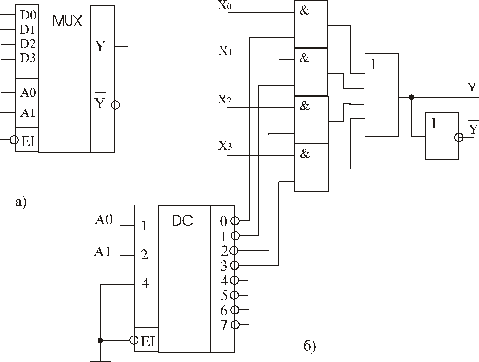
Рис. 3.4 Схематичне позначення та структура мультиплексора 4-1
На рис. 3.4.а показана схема мультиплексора 4-1, що з допомогою n=2 адресних сигналів 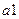 і
і 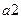 забезпечує вибір одного з
забезпечує вибір одного з 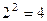 даних
даних 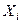 . Отже, логічна функція мультиплексора 4-1 має вигляд
. Отже, логічна функція мультиплексора 4-1 має вигляд
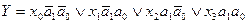 ( 3.3 )
( 3.3 )
Таку логічну залежність неважко абстрагувати для довільної кількості адрес:
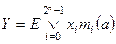 ( 3.4)
( 3.4)
де 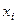 – вхідні інформаційні сигнали,
– вхідні інформаційні сигнали, 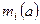 – мінтерми
– мінтерми 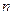 адресних змінних
адресних змінних 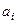 .
.
У серіях ЦТ зустрічаються мікросхеми мультиплексорів з різним числом адресних входів, найчастіше n=2,3,4,... При конструюванні пристроїв на мультиплексорах, слід мати на увазі, що в переважній більшості своїй мультиплексори комутують цифрові сигнали, хоча існують деякі мікросхеми мультиплексорів (найчастіше КМОН), які дозволяють комутувати й аналогові сигнали. Детальніше про особливості кожної конкретної мікросхеми слід ознайомитись з технічної документації на неї.
Для комутування (мультиплексування) великої кількості сигналів застосовують принцип каскадування. Приклад мультиплексування 8-ми розрядної шини даних каскадуванням двох мультиплексорів 4-1 показано на рис. 3.5.
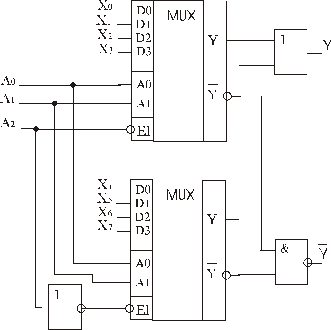
Рис. 3.5 Синтез мультиплексора 8-1 за допомогою мультиплексорів 4-1
Розподіл шини адрес здійснено аналогічно до принципу каскадування дешифраторів (рис.3.3)
За допомогою мультиплексорів можна реалізувати безліч найрізноманітних цифрових, а у деяких випадках цифро-аналогових схем. Наприклад, на базі мультиплексорів реалізуються: КП багатьох змінних, багатоканальні комутатори цифрових та аналогових сигналів, запам'ятовувальні пристрої, генератори послідовностей двійкових чисел, тощо. Крім згаданих прикладів застосування мультиплексор можна використовувати також і для перетворення паралельного коду, який подано на інформаційні входи, в послідовний, якщо з допомогою лічильника імпульсів потактно змінювати стан адресних входів мультиплексора. Цим способом можна також виконувати послідовне опитування сигналів на 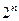 інформаційних входах мультиплексора.
інформаційних входах мультиплексора.
Демультиплексор (Demultiplexor: DMX) призначений для виконання оберненої функції мультиплексора, а саме - передачу (комутацію) сигналу з єдиного інформаційного входу на один з 2n виходів залежно від коду на n‑адресних входах. Демультиплексор можна реалізувати на дешифраторі з n‑входами, у якого вхід дозволу E використовується як інформаційний. Отже, демультиплексор - це розподілювач цифрових сигналів, керований двійковим входом.
Можливий варіант побудови демультиплексора 1-8 зображено на рис. 4.15. Паралельний код, що керує роботою демультиплексора, подають на входи дешифратора, які стають адресними, а виходи останнього під'єднують до входів кон'юнкторів.
У загальному випадку демультиплексор реалізує логічну функцію виду
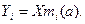 ( 3.5)
( 3.5)
З'єднані між собою, другі входи кон'юнкторів утворюють інформаційний вхід Х демультиплексора. Отже, на вихід 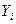 демультиплексор пропустить вхідний сигнал Х тільки через той кон'юнктор, на другому вході якого буде лог. 1, шо з'явиться з відповідного виходу дешифратора.
демультиплексор пропустить вхідний сигнал Х тільки через той кон'юнктор, на другому вході якого буде лог. 1, шо з'явиться з відповідного виходу дешифратора.
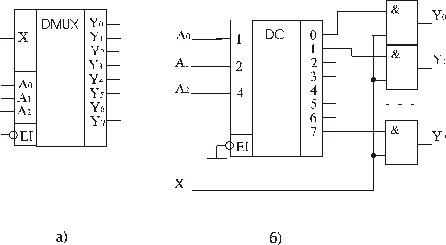
Рис. 3.6 Схематичне позначення та структура демультиплексора 1-8
Деякі мікросхеми ТТЛ, зокрема дешифратори К155ИД3, К155ИД4, К155ИД7, залежно від способу ввімкнення можуть працювати як демультиплексори. Функціональну дуальність мультиплексора і демультиплексора зручно використати для передачі інформаційних двійкових сигналів на відстань, наприклад, по телефонних лініях зв'язку та кабелях. В такій системі зв'язку функцію передавача-перетворювача паралельного коду в послідовний виконує мультиплексор, а функцію приймача-перетворювача послідовного коду у паралельний—демультиплексор. При наявності лінії керування обох перетворювачів забезпечується синхронна робота системи. Перевага такої системи передачі даних на відстань, незважаючи на її низьку швидкодію, полягає в економії затрат, які неминучі при паралельній передачі інформації.
3.3 Синтез комбінаційних пристроїв на дешифраторах
Дешифратори зручно використовувати в тих випадках, коли потрібно сформувати деяку кількість взаємно синхронізованих сигналів, або в загальному реалізувати деяку систему логічних функцій. При цьому дешифратор використовується у вигляді постійного запам’ятовувального пристрою (ПЗП), в якому містяться задані логічні функції. Для того, щоб детальніше зрозуміти вищесказане, розглянемо приклад. Нехай слід розробити цифрових пристрій, на вхід якого надходить циклічна двійкова послідовність Х: (0,1,2,3,4,5,0,1,2,3,4,5... і т.д.). У відповідь на це, розроблюваний пристрій повинен генерувати три синхронні послідовності, які в часовій формі виглядатимуть так (див. рис.3.7):
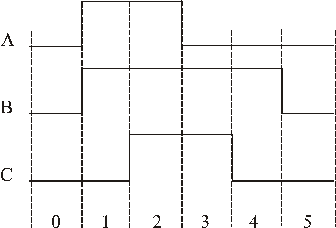
Рис. 3.7 Генеровані цифровим пристроєм сигнали
Система логічних функцій роботи даного пристрою матиме вигляд:
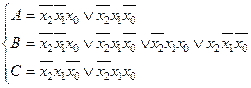 ( 3.6 )
( 3.6 )
Якщо подивитись на систему логічних функцій дешифратора (3.2), то стає зрозумілим, що там зустрічаються всі можливі терми системи (3.6). Залишається тільки об’єднати необхідні з них за допомогою зовнішніх диз’юнкторів. Схематично це буде мати наступний вигляд (див.рис.3.8):
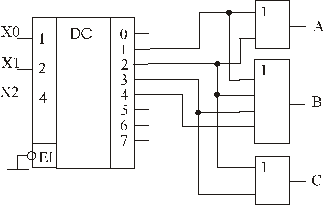
Рис. 3.8 Схема генератора сигналів представлених на рис.3.7
В іншій інтерпретації, робота пристрою може бути представлена так: сигнали Х надходять на вхід дешифратора послідовно, тому моменти часу 0,1,2,3,4,5 мають свої відповідні кодові послідовності, які на виході дешифратора перетворюються на сигнал "біжучої" в часі одиниці. Цей сигнал надходить на входи ЛЕ "АБО", які і формують відповідні вихідні сигнали.
3.4 Синтез комбінаційних пристроїв на мультиплексорах
Комбінаційні пристрої на мультиплексорах дозволяють реалізувати довільні логічні функції, і подібно до КП на дешифраторах, забезпечують зменшення кількості корпусів ІС на платі цифрового притсрою. Синтез КП на мультиплексорах полягає в тому, що задавши інформаційним входом лог.0 або лог.1 можна виключити або включити в логічну функцію той чи інший мінтерм, який визначається адресним кодом. Тому мультиплексор зручно застосовувати для реалізації довільної функції 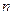 змінних, що подана в УДНФ. Оскільки вихід в мультиплексора один, то й логічну функцію можна реалізувати на ньому одну. Для реалізації системи логічних функцій слід використати каскадування декількох мультиплексорів. Методику синтезу розглянемо на прикладі.
змінних, що подана в УДНФ. Оскільки вихід в мультиплексора один, то й логічну функцію можна реалізувати на ньому одну. Для реалізації системи логічних функцій слід використати каскадування декількох мультиплексорів. Методику синтезу розглянемо на прикладі.
· Нехай слід розробити пристрій, на вхід якого надходить циклічна двійкова послідовність Х: (0,1,2,3,4,5,6,7... і т.д.). У відповідь на це, пристрій повинен генерувати кодову послідовність (01110010). Для цього зручно застосувати мультиплексор 8-1, інформаційні входи якого потрібно з’єднати з однойменними розрядами даного коду, як це показано на рис.3.9
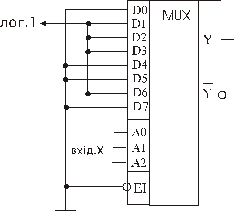
Рис. 3.9 Генератор кодової послідовності на мультиплексорі 8-1
Робота даного пристрою відбувається наступним чином: на адресні входи надходить двійкова послідовність Х: (0,1,2,3,4,5,6,7... ), що спричиняє послідовне під’єднання до виходу Y входів D0,D1,D2..., і як наслідок, на виході з’являється кодова послідовність "запрограмована" за допомогою подачі на ці входи лог.0 та лог.1.
3.5 Перетворювачі кодів
Вони призначені для перетворення одного різновиду цифрового коду в інший. Необхідність у таких перетворювачах для цифрових пристроїв пояснюється тим, що в деяких випадках технічно вигідніше і навіть точніше виконувати певні операції з допомогою інших кодів, а не лише одним двійковим кодом. Різновидів цифрових кодів є дуже багато, і кожен з них має свої переваги при застосуванні в своїх галузях.
Найчастіше виникає необхідність у перетворенні двійкового коду в інший, і навпаки, наприклад, у перетворенні прямого двійкового коду в обернений чи доповняльний код. Перетворювачі кодів необхідні насамперед для технічної реалізації різних арифметичних операцій над двійковими числами, а також для вводу та виводу числової інформації з однієї системи числення в іншу.
На відміну від дешифратора перетворювач кодів може формувати довільні двійкові числа. Кожному вхідному набору (слову) ставиться у відповідність вихідний набір (слово), а не унітарний код, як це має місце у дешифратора. Прикладом може бути перетворювач двійково-десяткового коду (8-4-2-1) у семирозрядний код, що призначений спеціально для керування семисегментним індикатором.
На рис. 4.10 показано спрощену схему ввімкнення двійково-десяткового перетворювача коду в семирозрядний код типу К514ИД1 для цифрового світлодіодного десяткового cемисегментного індикатора типу АЛС304А (АЛС324). Мікросхеми серії К514 допускають роботу з вихідними рівнями ЛЕ ТТЛ. Залежно від двійково-десяткового коду (8-4-2-1) на інформаційних входах дешифратора 4-7 та при 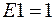 на відповідних виходах з’являються активні високі рівні, які викликають світіння відповідних сегментів індикатора, тобто зображення десяткових цифр від 0 до 9 згідно з поданою таблицею істинності (табл. 3.1).
на відповідних виходах з’являються активні високі рівні, які викликають світіння відповідних сегментів індикатора, тобто зображення десяткових цифр від 0 до 9 згідно з поданою таблицею істинності (табл. 3.1).
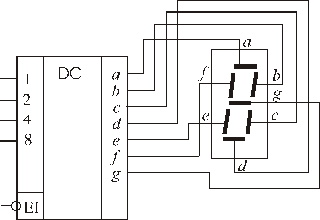
Рис. 3.10 Ввімкнення перетворювача коду 514ИД1 та семисегментного індикатора АЛС304А
Як видно з табл. 3.2, у даного перетворювача-дешифратора 4-7 є шість невикористаних вхідних кодових комбінацій - 1010, 1011, 1100, 1101, 1101, 1110, 1111. Для них функції можуть набувати значення 0 або 1. Їх можна, наприклад, використати для індикації малих букв латинського алфавіту, однак для цього слід сконструювати свій власний перетворювач двійкового коду в візуальний код семисегментного індикатора. Тому використання ІС типу К514ИД1 є зручним у випадку потреби відображення тільки цифрової інформації.
Таблиця 3.2 Коди для зображення десяткових цифр від 0 до 9
| Десяткова Цифра | ДДК (8-4-2-1) | Семирозрядний код | |||||||||
| Х3 | Х2 | Х1 | Х0 | a | b | c | d | e | f | g | |
| 0 1 2 3 4 5 6 7 8 9 | 0 0 0 0 0 0 0 0 1 1 | 0 0 0 0 1 1 1 1 0 0 | 0 0 1 1 0 0 1 1 0 0 | 0 1 0 1 0 1 0 1 0 1 | 1 0 1 1 0 1 1 1 1 1 | 1 1 1 1 1 0 0 1 1 1 | 1 1 0 1 1 1 1 1 1 1 | 1 0 1 1 0 1 1 0 1 1 | 1 0 1 0 0 0 1 0 1 0 | 1 0 0 0 1 1 1 0 1 1 | 0 0 1 1 1 1 1 0 1 1 |
До перетворювачів ДДК у семирозрядний код належать також мікросхеми дешифраторів, що мають також виходи з відкритими колекторами - КІ76ИД2(3), К155ПП5. Перетворювачі на мікросхемах К(М)155ИД8А(Б) і К(М)155ИД9 - це дешифратори ДДК для керування індикаторами, які складаються відповідно з 20 і 27 окремих світлодіодів, а дешифратор К(М)155ИД9 може працювати з напівпровідниковими індикаторами, що мають спільний анод. Все більшого застосування набувають перетворювачі ДДК у коди латинської (К155РЕ22) та російської (К155РЕ21) абетки, а також у код додаткових знаків-символів (К155РЕ23). Ці мікросхеми побудовані за принципом маскових ПЗП об'ємом (256х4)біт.
Розглянуті перетворювачі-дешифратори мають спільну особливість, що об'єднує їх в окремий клас так званих перетворювачів з неваговим (тобто без системи вагових коефіцієнтів у кожному розряді) перетворенням. Другий клас становлять перетворювачі кодів з ваговим перетворенням кодів. Сюди належать, зокрема, перетворювачі ДДК у двійковий код (К155ПР6), і навпаки (К155ПР7), що також побудовані за принципом маскових ПЗП, взаємні перетворювачі двійкового коду і коду Грея тощо.
3.6 Арифметичні пристрої
Розглянуті раніше КП виконують за законами булевої алгебри логічні операції над логічними змінними 0 і 1. Поряд з логічними операціями (заперечення, кон'юнкція, диз'юнкція) у цифровій техніці розглядаються також арифметичні дії над двійковими числами (додавання, віднімання, множення, ділення). Ці операції виконуються за допомогою арифметичних пристроїв, які є складовою частиною, функціональними вузлами мікропроцесорної та обчислювальної техніки. До них належать: суматори різних типів, віднімачі (субстрактори), перемножувачі, подільники, пристрої порівняння і порогові схеми (цифрові компаратори), пристрої виявлення парності (паритету) заданих чисел, арифметично-логічні пристрої тошо.
3.6.1 Арифметичні суматори
Це функціональні вузли, що здійснюють арифметичне додавання чисел. У цифровій техніці підсумовування виконується в основному над двійковими (рідше двійково-десятковими) числами. Додавання багаторозрядного слова за допомогою суматора здійснюється порозрядно з урахуванням переносу в сусідній старший рпзряд. Тому при побудові суматора необхідно враховувати не лише появу переносу в даному розряді, але й можливість одержання аналогічного переносу від сусіднього молодшого розряду.
За принципом побудови і типом використаних елементів розрізняють комбінаційні та накопичуючі суматори. Результати проміжного порозрядного додавання у накопичуючих суматорах зберігаються в елементарних комірках пам'яті, функцію яких викоиують тригери. Комбінаційні суматори не мають запам’ятовувачів. У них додавання двійкових чисел здійонюється позиційним кодои одночасно, як і у звичайних КП, результат на виході у комбінаційних суматорах зникає зразу після припинення дії вхідних сигналів. Тому до складу комбінаційних суматорів, як правило, входять вхідні та вихідні регістри, тобто пристрої, що здатні записувати чи перезаписувати проміжний результат підсумовування у послідовному або у паралельному коді.
Для додавання двійкових чисел можуть застосовуватись як одно-, так і багаторозрядні суматори, а сама процедура підсумовування може здійснюватись або послідовно, починаючи з молодпого розряду, або паралельно, коли всі розряди чисел додаються одночасно. Важливою ознакою паралельного суматора є спосіб організації переносу при підсумовуванні. Розрізняють суматори з послідовним, паралельним (наскрізним) та груповим переносом.
Як послідовні, так і паралельні суматори будуються на основі комбінаційного однорозрядного суматора, що складається з напівсуматора.
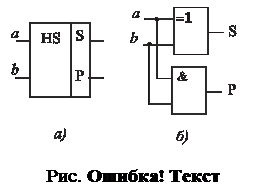 Напівсуматор - це пристрій (рис. 3.11), що має два входи (для доданків a і b) і два виходи (суми S і переносу P), і призначений для виконання арифметичних дій за правилами, що наведені у табл. 3.3. З таблиці істинності (табл. 4.5) видно, що напівсуматор виконує елементарне додавання двох однорозрядних двійкових чисел та сумовування отриманого результату з переносом у наступний старший розряд. Тому логічна структура напівсуматора має відображати стан обох виходів згідно з виразами:
Напівсуматор - це пристрій (рис. 3.11), що має два входи (для доданків a і b) і два виходи (суми S і переносу P), і призначений для виконання арифметичних дій за правилами, що наведені у табл. 3.3. З таблиці істинності (табл. 4.5) видно, що напівсуматор виконує елементарне додавання двох однорозрядних двійкових чисел та сумовування отриманого результату з переносом у наступний старший розряд. Тому логічна структура напівсуматора має відображати стан обох виходів згідно з виразами:
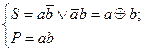 ( 3.7 )
( 3.7 )
Відповідно до наведених виразів логічна структура напівсуматора має містити два ЛЕ: суматор за модулем 2 і кон'юнктор, шо зображені на рис. 3.11.б.
Таблиця 3.3 Виконання арифметичних дій за правилами напівсуматора
| a | b | P | S |
| 0 0 1 1 | 0 1 0 1 | 0 0 0 1 | 0 1 1 0 |
Однак у логіці роботи напівсуматора не передбачено переносу з сусіднього молодшого розряду, тому напівпуматор може здійснювати додавання тільки у молодшому розряді двійкових чисел. Поява одиниці переносу при додаванні двох розрядів (числа і переносу) дещо змінює правила підсумовування двійкових чисел. Такий однорозрядний суматор потребує ще один (третій) вхід переносу з сусіднього молодшого розряду. Для цього служить так званий повний суматор.
Повний суматор (рис. 3.12) реалізує процедуру додавання двох однорозрядних двійкових чисел з урахуванням переносу з молодшого розряду. Тому він має три входи (ai, bi, Pi) і два виходи (Si і Pi+1). Логіка роботи повного суматора наведена у табл. 4.6, де ai, bi -доданки двійкових чисел в i-му розряді; Pi, Pi+1- переноси, відповідно з молодшого розряду i в сусідній старший розряд i+1; S -утворена сума в i-му розряді.
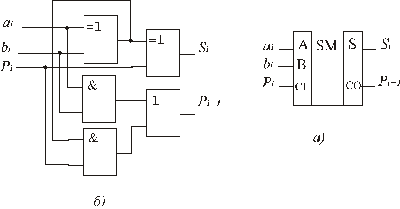
Рис. 3.12 Повний суматор
Таблиця 3.4 Виконання арифметичних дій для повного суматора
| ai | bi | Pi | Pi+1 | Si |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
Згідно з таблицею істинності (табл. 3.4) робота повного суматора двійкових чисел описується такими логічними виразами:
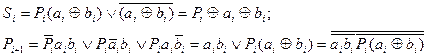 ( 3.8 )
( 3.8 )
За виразами (3.8) тепер можна побудувати повний суматор, структурна схема та умовне позначення якого зображені на рис. 3.12 (СІ -вхід переносу, від англ. Carry Input, а СO-вихід переносу, від англ. Carry Output).
Для додавання двох n-розрядних двійкових чисел A і B потрібно, очевидно, використати n однорозрядних повних суматорів. При цьому можуть бути два способи підсумовування - послідовне і паралельне. Застосування того чи іншого принципу підсумовування залежить від характеру вводу/виводу чисел та організації переносів багаторозрядного суматора.
3.6.2 Цифрові компаратори
Це арифметичні пристрої, що призначені для порівняння величин двох чисел, що подані у двійковому (двійково-десятковому) коді[*]. Найпростіший компаратор виявляє лише факт рівності або нерівності двох поданих на його входи n-розрядних чисел (операндів) А і В і формує на виході однобітовий сигнал. рівності (1) або нерівності (0) цих чисел. Слід зауважити відмінність цих пристроїв від аналогових компараторів, які порівнюють рівні напруг на їх входах, і за принципом дії є модифікованими операційними підсилювачами. Тому надалі розлядатимемо тільки цифрові компаратори.
Рівність, зокрема, двох однорозрядних операндів a і b визначається логічною операцією рівнозначності (див.у табл. 1.5 функцію f9):
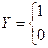
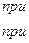
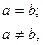
тобто логічною операцією виняткове АБО-НЕ, яка реалізується суматором-інвертором за модулем 2. Синтез однорозрядного компаратора рівності досить просто здійснюється у довільному базисі.
Порозрядну рівиість n -розрядних операндів найпростіше реалізувати за допомогою суматорів-інверторів за модулем 2 і кон’юнкторів, як це показано на рис. 3.13. Такий компаратор рівності порівнює окремі розряди n -розрядних чисел за формулою:
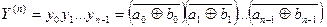 ( 3.9 )
( 3.9 )
Аналогічний результат одержується й при синтезі компаратора у базисі суматорів за модулем 2 та диз’юнктора. Якшо застосувати закои дуальності, вихідна функція такого компаратора описуватиметься виразом
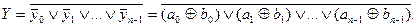 ( 3.10)
( 3.10)
Компаратори порівняння n-розрядних чисел можна будувати за двома принципами - логічним та арифметичним. Перший принцип (логічний) базується на синтезі за таблицею істинності, другий (арифметичний) - на 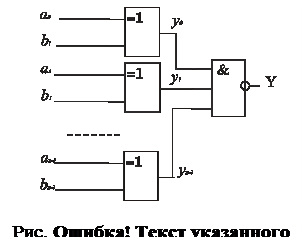 синтезі схеми, що виконує компарування дії віднімання і порівняння їх знаків. На рис.3.14.а показана схема чотирирозрядного компаратора, що реалізує арифметичний принцип порівняння. Даний цифровий компаратор створений на базі чотирирозрядного суматора. Функцію дешифратора нуля тут виконує ЛЕ 4АБО. Тільки при рівності всіх розрядів суми S0=S1=S2=S3=0 на виході 4АБО з’явиться 0, а після івертора 1, яка підтверджує рівність А=В. В інших випадках на виході 4АБО одиниця, яка стає дозволом для схеми збігу 2І.
синтезі схеми, що виконує компарування дії віднімання і порівняння їх знаків. На рис.3.14.а показана схема чотирирозрядного компаратора, що реалізує арифметичний принцип порівняння. Даний цифровий компаратор створений на базі чотирирозрядного суматора. Функцію дешифратора нуля тут виконує ЛЕ 4АБО. Тільки при рівності всіх розрядів суми S0=S1=S2=S3=0 на виході 4АБО з’явиться 0, а після івертора 1, яка підтверджує рівність А=В. В інших випадках на виході 4АБО одиниця, яка стає дозволом для схеми збігу 2І.
Промисловість випускає цифрові багаторозрядні компаратори як окремі вироби. Це в основному мікросхеми чотирирозрядних компараторів ТТЛШ - К555СП1, 531СП1 і КМОН - 564ИП2, 561ИП2, які мають, вбудовані інвертори для операнда В і додаткові три входи аналізу І>(А>B), I=(A=B), І<(А<В) (див. рис. 3.14.б). Останні призначені для утворення схеми нарощування розрядності операндів, тобто для каскадування послідовним або пірамідальним способом під’єднання однотипних мікросхем.
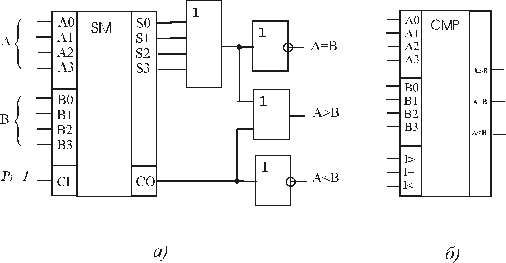
Рис. 3.14 Арифметичний принцип порівняння та позначення цифрового компаратора
3.6.3 Арифметико-логічні пристрої
Дня виконання над оперендами А і B як арифметичних, так і логічних операцій доцільно застосовувати мікросхеми універсальних арифметично-логічних пристроїв (АЛП), які можна знайти у складі серій ТТЛ і КМОН. Найчастіше вони мають чотирирозрядні входи операндів А і В і придатні для нарощування їх розрядності. Для виконання тих чи інших логічних або арифметичних операцій служать спеціальні керуючі входи. Подаючи на них чотирирозрядний код і задавши тип операції (арифметичної чи логічної), можна виконати за допомогою мікросхеми одну з 16 арифметичних або одну з 16 логічних операцій. Через широкі функціональні можливості мікросхеми АЛП входять до складу мікропроцесорів ЕОМ. У комплекті з АЛП випускають ще мікросхему, яка являє собою тракт групового переносу ддя виконання прискореного підсумовування багаторозрядних чисел. Самі АЛП при цьому відіграють роль чотирирозрядних груп, оскільки в основному промисловістю випускаються чотирирозрядні АЛП. До таких мікросхем АЛП належать із серій ТТЛ КІ55ИП3 (із схемою прискореного переносу К155ИП4), із серій КМОН 564ИП3 (відповідно 564ИП4). Для виконання більш складних за алгоритмом арифметичних та логічних операцій застосовують мікропроцесорні ВІС.
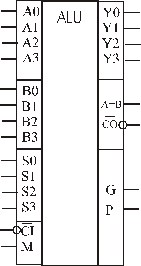
Рис. 3.15 Позначення ІС арифметико-логічного пристрою
Мікросхеми АЛП (К155ИП3 і 564ИП3) - це комбінаційні логічні схеми, що можуть виконувати арифметичні та логічні операції над чотирирозрядними операндами А і B з урахуванням або без урахування переносу Pi. На рис.3.15 зображене умовне схемне позначення мікросхеми АЛП* К564ИП3, яка функціонує згідно з табл. 3.5 (для випадку активних високих рівнів ([34]. АЛП для слів мав чотири пари входів А0-А3 і В0-В3 і чотири виходи Y0 –Y3, на яких фіксується результат арифметичної (при М=0) або логічної (при М=1) операції. Потрібну операцію (арифметичну чи логічну) вибирають за допомогою коду на входах S0 – S3.
Таблиця 3.5 Режими функціонування АЛУ типу К564ИП3
| S3 | S2 | S1 | S0 | M=1 | M=0 |
| 0 | 0 | 0 | 0 | 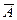
| 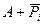
|
| 0 | 0 | 0 | 1 | 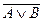
| 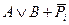
|
| 0 | 0 | 1 | 0 | 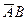
| 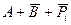
|
| 0 | 0 | 1 | 1 | 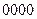
| 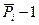
|
| 0 | 1 | 0 | 0 | 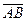
| 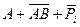
|
| 0 | 1 | 0 | 1 | 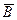
| 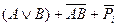
|
| 0 | 1 | 1 | 0 | 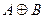
| 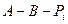
|
| 0 | 1 | 1 | 1 | 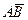
| 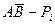
|
| 1 | 0 | 0 | 0 | 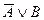
| 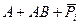
|
| 1 | 0 | 0 | 1 | 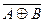
| 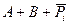
|
| 1 | 0 | 1 | 0 | 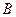
| 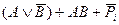
|
| 1 | 0 | 1 | 1 | 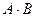
| 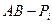
|
| 1 | 1 | 0 | 0 | 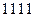
| 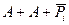
|
| 1 | 1 | 0 | 1 | 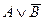
| 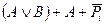
|
| 1 | 1 | 1 | 0 | 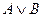
| 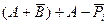
|
| 1 | 1 | 1 | 1 | 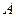
| 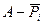
|
3.6.4 Програмовані логічні матриці
Програмовані логічні матриці (ПЛМ) в загальному розрізняють двох типів – комбінаційні і послідовнісні. Послідовнісні ПЛМ мають властивості комбінаційних + містять вбудовані регістри пам’яті. Останнім часом ця галузь цифрової техніки невпинно розвивається, кількість типів послідовнісних ПЛМ зростає мало не кожного року, структура їх щоразу ускладнюється, тому вони є предметом вивчення окремого курсу. Для програмування ПЛМ розроблені спеціальні вхідні мови, на зразок VHDL, AHDL, і т.д., тому ми розглянемо тільки елементарні положення ПЛМ.
Комбінаційна логічна матриця – це пристрій, який може бути представлений мережею взаємоперпендикулярних провідників, в місцях перетину яких знаходяться напівпровідникові елементи – діоди або транзистори, що ввімкнені через легкоплавкі перемички до відповідних провідників матриці.
Під час програмування логічної матриці перемички перепалюють імпульсами струму або зберігають у відповідності до необхідної таблиці, яка відображає необхідний рисунок програмування. Таким чином у комбінаційній ПЛМ може бути реалізована система з m бульових функцій до n вхідних змінних, що містять разом не більше як l терм (складових). В залежності від типу ПЛМ значення m,n,l відрізнятимуться. Структура комбінаційної ПЛМ наведена на рис.3.16.
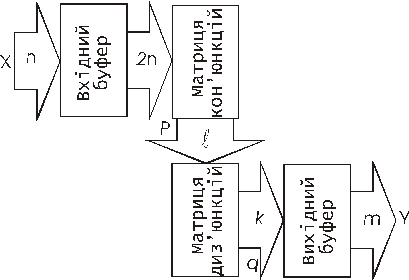
Рис. 3.16 Структура комбінаційної ПЛМ
ПЛМ складається з матриці кон’юнкцій створюють терми виду 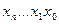 та матриці диз’юнкцій які виконують лог. операцію „АБО” над цими термами. Вхідний буфер крім буферування, здійснює ще й іверсію всіх змінних Х, тому вихідна шина буфера має 2n провідників.
та матриці диз’юнкцій які виконують лог. операцію „АБО” над цими термами. Вхідний буфер крім буферування, здійснює ще й іверсію всіх змінних Х, тому вихідна шина буфера має 2n провідників.

Рис. 3.17 Схематичне позначення ПЛМ
Позначення ПЛМ наведене на рис.3.17. Приклад типів комбінаційних ПЛМ: К556РТ1, К556РТ2. Їх основні параметри m=8, n=16, l=48. На даний час ці ІС слід вважати застарілими, в основному через високе енергоспоживання у порівнянні із сучасними зарубіжними взірцями, тому використовувати їх в сучасних розробках не рекомендовано.
Контрольні запитання по розділу
· Чи може у простого дешифратора бути активними декілька вихідних ліній?
· Будова дешифратора. Основні принципи.
· Будова мультиплексора. Основні принципи.
· Мультиплексори та демультиплексори. Основні відмінності.
· Як здійснюється каскадування дешифраторів?
· В чому полягає синтез комбінаційних пристроїв на основі дешифраторів?
· В чому полягає синтез комбінаційних пристроїв на основі мультиплексорів?
· Принцип дії цифрових компараторів.
· Будова напівсуматора.
· Будова повного суматора.
· Які функції може виконувати арифметико-логічний пристрій?
· Що таке ПЛМ?
· Відмінність між комбінаційними та послідовнісними ПЛМ.
4. ПОСЛІДОВНІСНІ ПРИСТРОЇ
4.1 Особливості функціонування послідовнісних пристроїв
Переважна більшість сучасних цифрових пристроїв є послідовнісними (ПП) або цифровими автоматами з пам’яттю, тобто такими, що складаються з комбінаційної частини (або КП) і елементів пам'яті - запам’ятовувачів інформації. Сама наявність запам’ятовувачів у ПП хоч і ускладнює його роботу, але й значно розширює функціональні можливості ПП. Разом з тим вони є причиною появи додаткової змінної - часу, який потрібно враховувати як при аналізі, так і при синтезі ПП.
Таблиця 4.1 Табличне представлення автомата Мура.
|
Вхідний набір Х | Стан і вихід | |||
| q0 | q1 | … | qk-1 | |
| y1 | y0 | … | yj | |
| X0 X1 … Xn-1 | q2 q0 … ~ | q0 q1 … q2 | … … … … | qi ~ … qj |
Як бачимо, автомат Мура, який задається табл.4.1, має виходи, які однозначно визначені його станами, і тому вони можуть бути вказані біля вершин графа. Для автомата Мілі, однак, потрібно вказувати пару Xi/Yj, бо їх ииходи залежать як від станів, так і від вхідних наборів.
Порівняно з іншими способами зображення логічного функціонування ПП графічний спосіб є найбільш наочний.
Приклад: Побудувати граф абстрактного автомата Mілі, що заданий сумісною таблицею переходів (табл. 4.2).
Таблиця 4.2 Cумісна таблиця переходів автомата Mілі
| {Xt} | q0t | q1t | q2t | q3t |
| 00 01 10 11 | q1/1 q2/0 q3/1 q0/~ | q1/0 q1/1 q3/0 q3/1 | q0/0 q3/~ q0/1 q2/1 | q3/1 q0/0 q0/0 q2/0 |
Розв’язання. Для зручності стани {qit} автомата позначимо просто цифрами, що відповідають номеру стану, і розмістимо їх в середині кружечків. Граф таблично заданого автомата показаний на рис. 4.1.
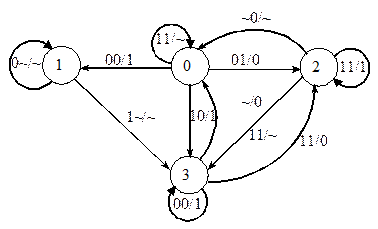
Рис. 4.1 Граф автомата Мілі у відповідності до таблиці 4.2
Зауважимо, що у даному прикладі є кількa однакових переходів станів, які відбуваються під дією різних вихідних сигналів. Це, зокрема, переходи q1t→ q1 – 00/0v01/1; q1t→ q3 – 10/0v11/1; q2t→ q0 – 00/0v10/1; q3t→ q0 – 01/0v10/0.
Оскільки ці пaри вхід/вихід при переході i→j мають байдужі розряди (0/1), їх зручніше зобразити так, як це ілюструє граф, а саме: q1t→ q1 – 0~/~; q1t→ q3 – 1~/~; q2t→ q0 – ~0/~; q3t→ q0 –~~/0.
4.2 Особливості синтезу послідовнісних пристроїв
Всі послідовнісні автомати або пристрої можна поділити на три класи: асинхронні потенціальні автомати, асинхронні імпульсні автомати та синхронні автомати.
До основних функціональних ПП, що виконані, як окремі інтегральні мікросхеми СІС або ВІС, належать регістри, лічильники, тощо.
Структурний синтез ПП зводиться до побудови такої схеми автомата, яка функціонує відповідно до заданих таблиць переходів і виходів автомата. Вихідними даними для структурного синтезу ПП є опис алгоритму його функціонування, згідно з таблицями станів заданий елементний базис ЛЕ і запам’ятовувачів iнформації, а у випадку побудови конструкції ВІС ПП - вимоги до електричних параметрів з урахуванням конструкторсько-топологічних особливостей реалізації вибраного елементного базису. Процес структурного синтезу ПП можна розкласти на такі етапи:
1) оцінка складності алгоритму і при необхідності каскадування ПП;
2) формалізований опис aлгоритму функціонування пристрою або його каскаду;
3) мінімізація станів пристрою i визначення кількості запам’ятовувачів;
4) кодування внутрішніх станів пристрою;
5) складання таблиць переходів, a також функцій збудження i виходів та мінімізація останніх;
6) перетворення мінімізованих функцій збудження i виходів до заданого функціонального безису ЛЕ i зaпам’ятовувачiв;
7) побудова структурної логічної схеми ПП;
8) тестування.
Критерієм якості економного способу кодування станів є простота схемної реалізації, яка передбачає мінімальне число ЛЕ. Цей спосіб кодування є ефективним особливо для синхронних ПП, бо наявність кіл синхронізації усуває у них такі недоліки, як змaгання (гонки) сигналів, що викликають ризик збою. Економний спосіб кодування полягає у тому, що суміжні кодові комбінації станів автомата відрізняються одна від одної тільки однієї цифрою (0 або 1).
Так само, як і у КС, у асинхронних ПП гонки можуть виникати через різні затримки у спрацюванні запам’ятовувачів інформації. Між синтезом тригера на основі ЛЕ і синтезом ПП на основі тригерів є певна різниця, яку треба враховувати у процесі проектування того чи іншого пристрою.
Логіка роботи будь-якого тригерa як послідовнісного автомата характеризується таблицями станів - переходів i виходів. Але враховуючи те, що тригер - це автомат Мура, у якого вихідна змінна уt+1 повторює значення його внутрішнього стану Qt+1 , можна обмежитись таблицею переходів тригера.
На основі таблиці переходів можна отримати функцію переходів тригера, тобто логічну функцію, яка показує зв’язок зміни стану тригера Qt→Qt+1 під дією комбінації вхідних сигналів. Якщо під вхідними сигналами Xit, тригера розуміти як iнформаційні, так i керуючі,сигнали, функцією переходів тригера є залежність Qt+1 = f(Qt, Xt), за якою, як і за таблицею переходів, можна визначити тип тригера. Як і у КП, функцію переходів тригера потрібно мінімізувати, наприклад, з допомогою карт Карно. Далі у заданому базисі ЛЕ можна будувати структуру тригера. Отже, для синтезу тригера у базисі ЛЕ досить мати мінімізовану функцію переходів тригера.
При синтезі послідовнісних схем на базі тригерів виникає обернена задача - треба визначити, при яких наборах вхідних змінних Xі той чи інший тригер перейде з відомого або заданого стану Qit у наступний стaн Qit+1 . Для цього служать таблиці переходів або матриці переходів тригера, які будуються зв принципом перебору всіх можливих переходів Qt→Qt+1 (їх є чотири: 0→0, 0→1, 1→0, 1→1). Цим переборам залежно від типу тригера відповідають конкретні комбінації вхідних сигналів, і в тому числі невизначені їх значення, які позначаємо тильдою “~”.
4.3 Тригер – найпростіший зaпам’ятовувальний пристрій
Спільним елементом всіх ПП є запaм’ятовувач бінарної iнформації. У ЦТ функцію найпростішого запам'ятовувача, що може зберігати 1 біт двійкової інформації (лог. 0 або лог. 1) виконує тригер[2]. Тригер як двостановий** зaпaм’ятовувач інформації хapактеризується значною функціональною гнучкістю. Поняття "тригер" охоплює безліч пристроїв, які суттєво відрізняються між собою схемним рішенням, функціональними ознаками, способом керування тощо. У цифрових системах радіоелектроніки тригер, крім зберігання інформації, може виконувати також функції перетворювача iнформації чи сигналів.
З точки зору теорії автоматів тригер як елементарний скінченний автомат характеризується такими властивостями:
· число вхідних змінних Xi залежить від типу тригера;
· число внутрішніх станів два (0 або 1), що відповідає одній змінній qi (прийнято позначати як Q );
· число вихідних змінних Yi одне, значення якого збігається із значенням стану Q(Yt+1 ≡ Qt+1); отже, тригер – це елементарний автомат Мура.
Тому, коли говорять про стан тригера, то розуміють логічний рівень сигналу на його прямому виході Q /поряд з прямим виходом Q тригер має ще iнверсний вихід 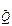 /. Якщо стан тригерa "1", це означає, що
/. Якщо стан тригерa "1", це означає, що 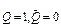 , якщо "0", відповідно
, якщо "0", відповідно 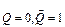 . Стан тригера може змінюватися під дією різних зовнішніх сигналів. Процес переходу тригера з одного стiйкого стану в інший відбувається стрибкоподібно і називається перемиканням тригера. Перемикання тригера складається з двох складових - iз встановлення інформації тригера у певний стан (0 або 1) під дією активного вхідного сигналу та із скидання , як правило в стан Q = 0, що відбувається під дією спеціального сигналу "скидання" i означає повернення тригера у пасивний (початковий) стан.
. Стан тригера може змінюватися під дією різних зовнішніх сигналів. Процес переходу тригера з одного стiйкого стану в інший відбувається стрибкоподібно і називається перемиканням тригера. Перемикання тригера складається з двох складових - iз встановлення інформації тригера у певний стан (0 або 1) під дією активного вхідного сигналу та із скидання , як правило в стан Q = 0, що відбувається під дією спеціального сигналу "скидання" i означає повернення тригера у пасивний (початковий) стан.
4.3.1 Загальна структура та класифікація тригерів
Виходячи iз загальних принципів побудови ПП, узагальнюючу структуру тригера можна зобразити з двох частин - комбінаційної схеми (КС) і елементарного двостанового запам’ятовувача, тобто власне тригера (див рис. 4.2). КС, на яку надходять ззовні або подаютьея по колах додатного зворотного зв’язку різні сигнали, виконує функції керування роботою та формування властивостей всієї схеми тригера. Певна комбінація взаємодії цих входів i визначає відмінність функціонування тригера, а отже, і його тип.
За характером дії вхідних сигналів входи тригера розрізняють: інформаційні і керуючі, які залежно від виконуваної ролі можуть бути дозволяючі та синхронізуючі.
На інформаційні входи тригера подають двійкову інформацію (Хі), яку він має зафіксувати у вигляді нуля або одиниці. На керуючі входи подаються сигнали, які виконують допоміжну функцію – саме з їх допомогою у потрібний момент можна виконати запис чи перезапис та зчитування записаної інформації. Зокрема, на виконавчі входи тригера подаються тактові або синхронізуючі сигнали, які встановлюють у КС момент запису чи зчитування, тобто перемикання тригера


Рис. 4.2 Узагальнююча структурна схема тригера
. Таким чином, встановлення або скидання тригера здійснюється при певній взаємодії вхідних сигналів, які саме роблять його активним або пасивним.
Нижче наведений перелік можливих входів умовного тригера за їх функціональним призначенням.
Інформаційиі входи:
R,K – входи окремого встановлення (скидання) тригера в стан 0 (R - з англ. Reset - скидати, очищувати; K - з aнгл. Kill -раптово вимикати), у даному випадку iз стану 1 в 0;
S,J – входи окремого встановлення тригера у стан 1 (S - з англ. Set – установлювати; J - з англ. Jerk– раптово вмикати), в даному випадку iз стану 0 в 1;
D – вхід встановлення тригера у cтан 1/0 (D - з англ. Delay – затримка);
T – вхід перемикання/встановлення /1/ i скидання /0/ тригера, або лічильний вхід (T - з англ. Toggle – перевертати).
Керуючі входи:
V,E - входи дозволу запису або зчитування iнформації ( V — з англ. Valve – клапан; Е - з aнгл. Епаblе – дозвіл);
С - виконавчий вхід для тактових чи синхронізуючих iмпульсів (С - з aнгл. Сlоск – годинник).
У iнтегральному виконанні тригер - це конструктивно єдиний функціональний вузол, тобто мікросхема, яка може бути виготовлена за певною технологією (ТТЛ, КMОН…). З точки зору схемотехніки тригер – це електронна схема, шо має два стійких стани (високий або низький рівень), які встановлюються при подачі відповідної комбінації сигналів інформації на керуючі входи схеми і які після закінчення дії цих сигналів зберігаються протягом заданого часу.
Тип тригера визначається функціональною залежністю між сигналом нa виході і сигналами на входах. Ця залежність може бути подана різними способами: аналітичнo, графічно, часовими діаграмами, таблицями станів.
У iнтегральному виконанні в основному зустрічаються серед одновходових D- i T-тригери, серед двовходових – RS- і JК -тригери, а серед універсальних - JК(RS) -тригер. Інші типи тригерів, яких досить багато, можуть бути побудовані у базисі різних ЛЕ.








