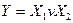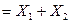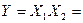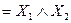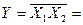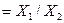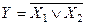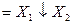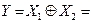1. Математичні основи цифрової техніки
0. ВСТУП
Цифрова електроніка, це розділ електроніки, що ввійшов в повсякденне життя починаючи з 80-х років ХХ століття. Цифрові CD та DVD програвачі, мобільні телефони, комп’ютери, цифрові фото- та кіно камери – ось далеко не повний перелік всіх приладів, в яких основне ядро процесів виконане з використанням цифрової техніки. Розвиток технологій виробництва інтегральних схем (ІС) призвів до значного збільшення швидкості їх роботи, що дозволило викоритати теоретичну базу цифрової техніки там де раніше панували винятково аналогові системи.
Крім таких переваг, як економічність, конструктивна технологічність, і т.ін., є ще й принципи цифрової обробки сигналів, які дозволяють досить просто і точно реалізувати складні алгоритми, які не під силу аналоговій техніці. Останні покоління ЕОМ реалізовані на основі мікропроцесорних: інтегральних схем, що містять на напівпровідниковій пластині площею не більше 1 см2 окремі блоки, а то і цілі пристрої. Малі габаритні розміри і низьке енергоспоживання та вартість таких машин дозволяють вбудовувати їх в різні пристрої та системи радіоелектроніки, причому продуктивність сучасних мікроЕОМ призначених для таких цілей співрозмірна з продуктивністю персональних ЕОМ кінця 90‑х рр. минулого століття. Це дозволяє, наприклад, вбудувати в сучасну пральну машину надвичайно складний алгоритм роботи, який враховуватиме велику кількість параметрів процесу, що в кінцевому випадку призводить до зменшення енерговитрат та підвищення якості роботи та збільшення надійності.
"Основи цифрової техніки" є базовим курсом для вивчення таких дисциплін як "Мікропроцесорні пристрої", "Мікроконтролери", тощо.Тому доскональне вивчення основ цифрової техніки, є важливим завданням, до якого майбутному спеціалісту слід віднестись з особливою відповідальністю. В свою чергу маю сподівання що пропонований конспект лекцій зможе допомогти йому в цьому нелегкому процесі. Разом з тим слід відзначити, що конспект в силу обмеженості його об’єму не може повністю відображати всієї різноманітності сучасної цифрової техніки, тому для більш грунтовного розуміння предмету слід ознайомитись із літературою наведеною в кінці конспекту. Крім того, дуже корисним є вивчення технічної документації на цифрові ІС провідних світових виробників Texas Instruments, Motorola, Philips, Toshiba, National Semiconductor яка вільно розповсюджується за допомогою мережі Internet. Інший шлях самовдосконалення – це набуття практичного досвіду в цифровій схемотехніці. Зараз цей процес теж є значно простіший ніж ще 20 років тому, внаслідок наявності значної кількості "комп’ютерних тренажерів" – симуляторів роботи електронних схем. Для роботи студентів під час вичення курсу "Основи цифрової техніки" з цією метою зручно користуватись такими симуляторами як Spectrum MicroCAP, та Proteus. Проведене "дослідження" роботи цифрових пристроїв за їх допомогою принесе користь при виченні та зекономить значну кількість часу.
1. МАТЕМАТИЧНІ ОСНОВИ ЦИФРОВОЇ ТЕХНІКИ
1.1 Відображення інформації у цифровій техніці
Інформація (від лат informatio – роз’яснення, виклад, обізнаність) як об’єкт передання, поширення, перетворення, зберігання чи безпосереднього виконання потребує матеріального носія. Таким носієм інформації у радіоелектроніці е електричний сигнал - напруга або струм. Як функція часу електричний сигнал може бути неперервним або дискретним. Неперервний (або аналоговий) сигнал у заданому діапазоні зміни аргументу t набуває довільної множини значень, дискретний сигнал - лише при певних значеннях аргументу nt (де t - інтервал дискретності, n = 0,1,2,...). Тому дискретний сигнал може мати тільки обмежене (скінченне) число рівнів напруги або струму. Ці рівні зафіксовані на однакових інтервалах часу nt , що називаються тактами (в музиці, до речі, тактами також називають інтервали часу, хоча там вони можуть бути не обов’язково однакової розмірності).У ЦТ основним носієм інформації є дискретний сигнал. Щоб він адекватно відображав інформацію, яка може бути подана у найрізноманітніших формах (числами, буквами, сигналами різної природи чи якимись символами), число рівнів і значення їх величин мають підпорядковуватися певній системі відліку, тобто системі числення, що характеризується певною сукупністю символів (алфавітом) і правил. Людина у повсякденному житті користується десятковою (арабською) системою числення, що складається з 10 цифр (0...9). Здавалося б, що й для відображення інформації з допомогою дискретного сигналу найкраще підходить десяткова система числення - досить лише мати шкалу з десяти однакових за величиною рівнів (квантів) напруг. Проте вона не стала основною в ЦТ з багатьох причин. Цифрові сигнали, створені на основі десяткової системи числення, технічно реалізувати досить важко і тому економічно невигідно, бо такого типу цифрові пристрої повинні мати десять рівнів напруги.
Найпростішою з усіх позиційних систем числення є двійкова , або бінарна система, що складається з двох цифр: 0 і 1. Звідси й походження слова-терміна "біт" , що означає "двійкова цифра” тобто 0 або 1. Двійкова система дозволяє найефективніше відобразити інформацію з допомогою електричних цифрових сигналів, якщо, наприклад, низький рівень напруги або відсутність імпульсу позначити як логічний нуль (лог. 0), а високий рівень напруги або наявність імпульсу - як логічну одиницю (лог.1).
Всю інформацію, таким чином, можна зобразити у вигляді ланцюжка 0 і 1, тобто набору чи комбінації бітів, що називають словом. Отже, послідовність 0 і 1 певної довжини (слово) може зображати будь-яке число, кожний розряд (біт) якого з одиницею інформації.
Задана кількість двійкових розрядів - бітів може не відповідати обсягу інформації, яка також вимірюється у бітах. Це дуже часто є причиною непорозумінь (через плутання цих двох різних понять). У цифровій та обчислювальній техніці 1 біт означає один двійковий розряд - символ, що може набувати лише ціле число, тобто двійкове n - розрядне число, що дорівнює n біт. Але щодо обсягу інформації n-бітне число не обов’язково може мати n біт інформації, воно цілком може дорівнювати, наприклад, 0.76 біт або 0.1 біт. Як правило, чим менше число бітів (як двійкових розрядів) використовується для відображення певної інформації, тим більша густина інформації. Наприклад (див.таб.1.1):
Таблиця 1.1 Однакова кількість інформації в різнопозиційних числах
| число з 4 позиціями | число з 1 позицією | число з 2 позиціями |
| 0000 | 0 | 00 |
| 0001 | 1 | 01 |
| 0010 | 2 | 10 |
| 0100 | 3 | 11 |
З допомогою двійкових чисел у цифровій та мікропроцесорній техніці зображаються дані - відомості, факти тощо, все те, що необхідно для виконання певної дії.
Таблиця 1.2 Кодування в поширених системах числення
| “2” | “8” | “10” | “16” |
| 0 1 10 11 100 101 110 111 1000 1001 1010 1011 1100 1101 1110 1111 10000 10001 ….. 11001 11010 11011 | 0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 17 20 21 …. 31 32 33 | 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 ….. 25 26 27 | 0 1 2 3 4 5 6 7 8 9 А B C D E F 10 11 ….. 19 1А 1В |
Дані подаються у такому (формалізованому) вигляді, що після перетворення у фізичний носій інформації вже у вигляді цифрового сигналу їх можна передавати, обробляти і зберігати за допомогою технічних носіїв чи засобів. Тому дуже часто замість слова "дані" вживається слово "інформація". Набір правил, що розкриває спосіб зображення даних з допомогою умовних знаків чи символів, називається кодом . Носіями інформації в електронних обчислювальних пристроях (ЕОП) є електричні сигнали, найчастіше — напруги. Інформація обробляється в цифровій формі. Кожній цифрі ставиться у відповідність визначений рівень сигналу.
Одиницею зображення даних, а також обміну даними, якою як єдиним цілим оперують між собою окремі цифрові пристрої чи вузли, є восьмирозрядне (восьмибітне) двійкове число - байт. Отже, 1 байт = 8 біт, і, очевидно, що з допомогою такого слова можна передати одне з 28 = 256 різних повідомлень, тобто можна, наприклад, закодувати текст якоюсь мовою, де кожному символу (букві, розділовому знаку, цифрі тощо) має відповідати одна кодова комбінація з 8 біт, або 1 байт. На практиці доцільно знати і вміти користуватися (наприклад, для визначення обсягу пам’яті ЕОМ) такими одиницями інформації.
Систем числення може бути безліч. (Поряд із згаданими системами у пристроях ЦТ можна зустріти й такі, як, наприклад, трійкова (Р=З). Очевидно, що вибір тої чи іншої системи числення залежить від певних критеріїв, які мають виконуватись для забезпечення оптимального результату. В загальному довільне число А у позиційній системі числення з постійною основою Р може бути виражене числовим рядом:
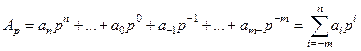 ( 1.1)
( 1.1)
де 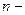 число знаків до коми;
число знаків до коми; 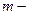 число знаків після коми;
число знаків після коми; 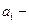 число в і-му розряді;
число в і-му розряді; 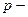 вага і-го розряду;
вага і-го розряду;
Двійкова система має набір цифр {0,1}, тому 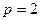 . Довільне число в А2 у двійковій системі можна зобразити виразом (1.1), результат обчислення якого – представлення цього числа в десятковій системі числення. Наприклад:
. Довільне число в А2 у двійковій системі можна зобразити виразом (1.1), результат обчислення якого – представлення цього числа в десятковій системі числення. Наприклад:
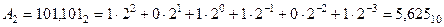
Для практичних розрахунків слід запам’ятати значення перших 13-ти розрядів цифр двійкової системи числення:
20=1, 21=2, 22=4, 23=8, 24=16, 25=32, 26=64, 27=128,
28=256, 29=512, 210=1024, 211=2048, 212=4096;
Шістнадцяткова система має набір цифр {0,1,2,3,4,5,6,7,8,9,А,B,C,D,E,F}, тому 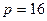 .При цьому великими буквами латинського алфавіту зображені цифри 10,11,12,13,14,15 (10). Наприклад:
.При цьому великими буквами латинського алфавіту зображені цифри 10,11,12,13,14,15 (10). Наприклад:
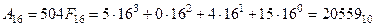
Для практичних розрахунків слід запам’ятати значення перших 6-ти розрядів цифр шістнадцяткової системи числення:
160=1, 161=16, 162=256, 163=4096, 164=65535, 165=1048576
Десяткова система числення, якою користуємось у повсякденному житті, не є найкращою з точки зору її технічної реалізації у цифрових пристроях. Відомі на сьогодні елементи, що мають десять стійких станів, щоб розрізнити всі десять символів (рівнів), наприклад, декатрони, мають невисоку швидкодію та складні для виготовлення. Отже, виникає закономірне питання: яка система числення найкраща? Вчені довели, що раціональною з точки зору мінімальних витрат умовного обладнання є система числення з основою Р»2.72»3. Отже, трійкова система краща за двійкову. Однак з’ясувалося, що за такими характеристиками цифрових пристроїв, як швидкодія, об’єм пам’яті, техніка виконання арифметичних та логічних операцій, найкращою е двійкова система числення.
Розглянемо, чому крім десяткової та двійкової систем числення в цифровій схемотехніці використовуються ще й такі системи числення, як вісімкова, шістнадцяткова і т. ін. Справа в тому, що якщо нас цілком влаштовує десяткова система, а для цифрового пристрою (мікропроцесорів, ЕОМ тощо) - виключно двійкова, бо там інформація обробляється тільки за допомогою нулів і одиниць, то проміжною, сполучною ланкою між нами і цифровим пристроєм має бути така система числення, яка була б найзручнішою як для взаємного переводу обох систем, так і для забезпечення простої технічної реалізації процедури. Для цього власне використовують проміжні системи числення - коди, за допомогою яких можна уникнути довгих ланцюжків з нулів та одиниць, які властиві двійковій системі. До таких систем кодування належить двійково-десятковий код (ДЦК).
Особливість ДДК полягає в тому, що кожній десятковій цифрі даного розряду відповідав чотирибітове (група з чотирьох бітів) двійкове число - тетрада. Наприклад, об’єднання двох тетрад дає можливість зобразити двозначне десяткове число, а з точки зору інформативності - реалізувати 16х16 - 256 двійкових комбінацій. При такому числі комбінацій можна закодувати не тільки 80 різних друкованих знаків клавіатури друкарської машинки, але й усі букви латинського алфавіту, розділові знаки, різні символи тощо.
Але при перетворенні десяткових чисел ДДК має надлишковість, бо при групуванні тетрадами шість комбінацій відпадає. Водночас при групуванні тріадами (трьома бітами), навпаки, інформативність падає. Цей факт і пояснює зручність шістнадцяткової системи числення, бо для ДЦК як разі потрібно 16 бітових комбінацій, які повністю забезпечує одна тетрада (11112=152). Зрозуміло, що при групуванні тріадами найзручнішою буде вісімкова система числення - там як раз вистачає 8 бітових комбінацій (1112=710)
Треба мати на увазі, що обидва коди - "16" і "8" - це тільки спосіб зображення двійкових чисел, якими оперують цифрові пристрої та мікропроцесори. Однак з точки зору інформатики код "16" має більші можливості, ніж код "8". Перевага коду "16" над кодом "8" ще в тому, що мікропроцесори маніпулюють словами, які залежно від функціональних можливостей можуть мати набори з 4, 8, 16 або 32 біт.
ДДК називають ще кодом 8-4-2-1, бо ці цифри відповідають вагам розрядів однієї тетради відповідно 23 (старшого розряду), 22, 21 і 20 (молодшого розряду). До двійково-кодованої десяткової системи числення належать й інші системи кодування.
При синтезі таких комбінаційних цифрових пристроїв, як перетворювачі кодів, що призначені для перетворення одного коду в інший, необхідно мати дані про різновиди цих систем кодування.
У табл. 1.3 зведені найбільш поширені в ЦТ різновиди позиційних кодів. До них належать ДДК 8-4-2-1, код 2-4-2-1 (або код Айкена), код з лишком 3 (або код [8-4-2-1]+З), код Грея та циклічний код Джонсона.
ДДК 8-4-2-1, який утворений зображеннями кожної десяткової цифри вагами 23-22-21-20, в найбільш поширеним, тому його найчастіше застосовують для переводу в інший код.
ДДК з лишком 3([8-4-2-1]+З) застосовують для кодування декад при двійково-десятковому зображенні чисел. Особливістю цього коду є те, що всі тетради мають значення на три одиниці більше від тетради коду 8-4-2-1.
Таку властивість самодоповнення має код Айкена (2-4-2-І). Для цього коду ваги розрядів тетради відповідно дорівнюють 21-22-21-20. Таблиця кодування, як видно з табл. 2.2, поділяється на дві частини: 0-4 -_це тетради, що повторюють еквіваленти; 5-9 – кожна тетрада у ДДК має лишок +0110. Така властивість коду Айкена дозволяє довільну цифру одної частини таблиці перетворити на її доповнення до 9 простим інвертуванням.
Особливе місце серед позиційних систем кодування посідають код Грея і циклічний код Джонсона. Це спеціальні коди, які мають непостійні ваги розрядів. Якщо у двійковому коді при переході від зображення одного числа до зображення наступного може відбуватись одночасна зміна цифр у кількох його розрядах, то в кодах Грея і Джонсона сусідні числа відрізняоться цифрою (1 або 0) тільки в одному розряді. Така особливість цих кодів запобігає появі джерела помилки у роботі апаратури у тих випадках, коли здійснюється послідовний перехід (зміна) числа з одного такту в наступний (наприклад, від 6 до 5),
У циклічному коді Джонсона перехід до наступного числа здійснюється шляхом послідовної заміни 0 на 1 до заповнення всіх розрядів одиницями, а потім заміною 1 на 0 до заповнення нулями. Помилки за допомогою кода Джонсона виявляються тоді, коли у "хвилі нулів" цього коду з’являється одна або кілька одиниць, а в "хвилі одиниць" - відповідно один або кілька нулів.
Окреме місце у ЦТ займає кодування алфавітно-цифрової інформації. Сюди належить текстова інформація, що являє собою послідовність алфавітно-цифрових символів, кожний з яких підлягає кодуванню. Щоб не було подвійного тлумачення, тобто щоб кожному символу відповідав тільки один код, застосовують спеціально призначені для цього стандартні коди. Зокрема, найчастіше в ЕОМ типу ІВМ застосовують код ASCII (American Standard Code of Information Interchange-американський стандартний код обміну інформацією), де, наприклад, десятковому числу 1 відповідає код 00010000(25) числу 2 - код 00010001, числу З - код 00010010 тощо, а букві А - код 00011000, букві В код 00011001, букві С - код 00011010 і т. ін.
Таблиця 1.3 Приклади двійкових кодів
| Дес. цифра | ДДК 8-4-2-1 | ДДК 2-4-2-1 | ДДК /8-4-2-1/+3 | Код Грея | Код Джонсона | Обчисл. код двійков. числа | Доповняльний код двійкового числа |
| 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 ….. | 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 0001 0000 0001 0001 0001 0010 0001 0011 0001 0100 0001 0101 0001 0110 0001 0111 …... …… | 0000 0001 0010 0011 0100 1011 1100 1101 1110 1111 0001 0000 0001 0001 0001 0010 0001 0011 0001 0100 0001 1011 0001 1100 0001 1101 …… …... | 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 0001 0011 0001 0100 0001 0101 0001 0110 0001 0111 0001 1000 0001 1001 0001 1010 …… …... | 0000 0001 0011 0010 0110 0111 0101 0100 1100 1101 1111 1110 1010 1011 1001 1000 11000 11001 ……. | 00000 10000 11000 11100 11110 11111 01111 00111 00011 00001 00000 10000 11000 11100 11110 11111 01111 00111 ……. | ….11111 11110 11000 11100 11110 11111 01111 00111 00011 00001 00000 10000 11000 11100 11110 11111 01111 00111 …… | ….00000 11111 11110 11101 11100 11011 11010 11001 11000 10111 10110 10101 10100 10011 10010 10001 10000 01111 …… |
1.2 Перетворення числової інформації
У процесі перетворення інформації, яку несуть цифрові сигнали, у цифровій системі (пристрої) виникає необхідність переводу чисел з однієї системи числення в іншу еквівалентну систему. Це означав що, наприклад, десятковому числу А має відповідати двійкове число А2
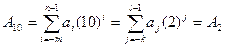 (1.2)
(1.2)
де aj = 0,1,2,...,9 - цифра в і-му розряді (m+n) -розрядного числа А10; аj=0 або aj=1 – цифр в j-му розряді (k+l) -розрядного двійкового числа A2 .
Перевід чисел з будь-якої позиційної системи числення у код "10" вже розглядався у підрозд.1.1. Для цього досить скористатися виразом (1.1), з допомогою якого розрахована сума ряду дає шуканий результат.
Розглянемо тепер перевід чисел у різних системах числення. Загальним правилом переводу числа з однієї системи числення до іншої е виконання таких послідовних кроків:
1) ділення в цілих числах заданого числа AР на основу Р тої системи, в яку переводиться дане число АР ;
2) якщо частка не дорівнює нулю, її слід взяти за нове число і повторити операцію п.1; якщо частка дорівнює нулю, перейти до п.3;
З) виписати всі остачі у зворотному порядку, починаючи з останньої, і взяти їх за цифри шуканого числа an-1 an-2 … a1 a0
За такими самими правилами виконуються взаємні перетворення (переводи) в інших системах числення. Тільки при цьому ділити або множити потрібно на число, яке дорівнює основі тієї системи числення, до якої треба перейти. Розглянемо приклад переводу числа 11810 з десяткової системи числення в двійкову:
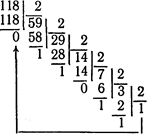
Записуючи неподільну частку і залишки в порядку, зворотному їхній появі, знаходимо що 11810=11101102
1.3 Двійкова арифметика
У цифрових та мікропроцесорних пристроях над двійковими числами виконуються як логічні, так і арифметичні операції. Арифметичні операції (додавання, віднімання, множення, ділення) над двійковими числами здійснюються (реалізуються) з допомогою спеціальних алгоритмів, які не використовуються у десятковій системі числення. У цих алгоритмах переважає операція додавання як додатних, так і від’ємних чисел, яку досить просто реалізувати.
Цифрові пристрої оперують тільки цілими і дійсними числами. Останні можуть бути подані з фіксованою або з плаваючою комою (точкою) (2;4). Незалежно від форм зображення знаки дійсних чисел "+" і "-" в ЦТ кодують цифрами - відповідно нулем (0) і одиницею (1).
Основною арифметичною операцією, яка використовується в цифрових пристроях для виконання різних обчислень, е операція алгебраїчного додавання двійкових чисел. Операція віднімання легко виконується через додавання, якщо змінити знак від’ємника на протилежний, а саме: А-В=А+(-В). Операції множення і ділення також виконуються з допомогою операції додавання та деяких логічних дій при застосуванні зсуву часткових результатів ліворуч або праворуч
Зупинимось на операції додавання двійкових чисел.
Операція додавання в цифрових пристроях виконується порозрядно, починаючи з молодших розрядів доданків. При цьому в кожному одноіменному розряді доданків підсумовуються відповідні цифри та переноситься попередній розряд суми. Додавання молодших розрядів двійкових чисел здійснюється лише з двома доданками:
· 0+0=0; 0+1=1; 1+0=1; 1+1=10,
де у числі 10 цифра 1 - перенос у наступний (старший) розряд.
Пристрій, що виконує операцію додавання двійкових чисел, називається суматором, а пристрій, що реалізує підсумовування молодших розрядів двійкового числа, - напівсуматором. Порозрядне підсумовування двох чисел як суматор, так і напівсуматор виконують за модулем 2 згідно з правилом 0Å0=0; 0 Å 1 = 1; 1 Å 0 = 1; 1 Å 1 = 0, яке це застосовують для порівняння двох чисел.
Для виконання операції додавання від’ємних чисел застосовуються спеціальні коди - обернений та доповняльний. Обернений код 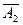 від’ємного числа А2 отримується при інвертуванні всіх цифр у кожному розряді, тобто заміні нуля одиницею, одиниці нулем, а у знаковому розряді ставиться одиниця. Отже, обернений код числа А10 =-28 буде
від’ємного числа А2 отримується при інвертуванні всіх цифр у кожному розряді, тобто заміні нуля одиницею, одиниці нулем, а у знаковому розряді ставиться одиниця. Отже, обернений код числа А10 =-28 буде 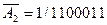 . Якщо виконувати операцій
. Якщо виконувати операцій 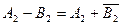 ,тобто зображати від’ємне число В2 оберненим кодом
,тобто зображати від’ємне число В2 оберненим кодом 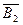 , може виникнути одиниця переносу, яку потрібно додати до молодшого розряду одержаної суми. Однак цю операцію, яка називається циклічним переносом, технічно реалізувати не вигідно, бо вона вимагає ще однієї операції додавання, що істотно збільшує час виконання дії. Тому для додавання від’ємних чисел перевага надається доповняльному коду числа
, може виникнути одиниця переносу, яку потрібно додати до молодшого розряду одержаної суми. Однак цю операцію, яка називається циклічним переносом, технічно реалізувати не вигідно, бо вона вимагає ще однієї операції додавання, що істотно збільшує час виконання дії. Тому для додавання від’ємних чисел перевага надається доповняльному коду числа 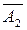 , який утворюється від оберненого додаванням одиниці до його молодшого розряду. При цьому відпадає необхідність у циклічному переносі одиниці та ще одного додавання. У випадку переповнення у знаковому розряді одиниця переносу просто відкидається і не враховується. Тому всі від’ємні числа, які використовуються для виконання різних арифметичних дій, подають у доповняльному коді. Отже, доповняльний код
, який утворюється від оберненого додаванням одиниці до його молодшого розряду. При цьому відпадає необхідність у циклічному переносі одиниці та ще одного додавання. У випадку переповнення у знаковому розряді одиниця переносу просто відкидається і не враховується. Тому всі від’ємні числа, які використовуються для виконання різних арифметичних дій, подають у доповняльному коді. Отже, доповняльний код 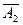 від’ємного n-розрядного числа А2 одержується з оберненого
від’ємного n-розрядного числа А2 одержується з оберненого 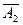 як
як 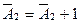 (у молодшому розряді), де
(у молодшому розряді), де 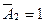 ,
, 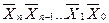 -від’ємне число в оберненому коді.
-від’ємне число в оберненому коді.
Якщо у знаковому розряді суми отримано одиницю, тобто результат від’емний, значення отриманого числа є у доповняльному коді, а якщо - нуль, результат додавання отримано у прямому коді. Сума доповняльних кодів двійкових чисел має доповняльний код результату. Отже, віднімання чисел довільного знака можна звести до операції додавання:
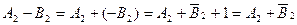
1.4 Основні поняття та закони бульової алгебри
У зв’язку з двійковим зображенням цифрових сигналів, що набувають тільки двох значень /0 і 1/, найзручнішим математичним апаратом для аналізу та синтезу цифрових систем є алгебра логіки (бульова алгебра). У бульовій алгебрі символи 0 і 1 характеризують стани змінних та їх функцій і тому не можна розглядати ці символи як арифметичні числа. Алгебра логіки - це алгебра станів, а не алгебра чисел, і їй властиві, на відміну від звичайної алгебри- логічні дії над станами.
Основне поняття алгебри логіки - висловлення, тобто речення, в якому міститься суть (сенс) твердження істинності або його заперечення (хибності). Будь-яке висловлення можна позначити символом, наприклад, X або У , і вважати, що, Х = 1 або У = 1, якщо висловлення істинне, а X = 0 або У=0, якщо висловлення неістинне (хибне). Оскільки будь-яка змінна (або її функція) може мати стан 0 або 1, в алгебрі логіки кожній двійковій змінній ставиться у відповідність обернена до неї (інверсна) змінна, така, що якщо Х=0, то 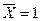 , а якщо
, а якщо 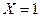 , то
, то 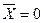 . Подвійне заперечення дав аргумент, тобто
. Подвійне заперечення дав аргумент, тобто 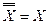 . Риска "-" над змінною Х означає, що над змінною
. Риска "-" над змінною Х означає, що над змінною 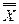 здійснено операцію логічного заперечення. Ця елементарна і дуже важлива у бульовій алгебрі логічна операція називається інверсією (логічним запереченням). Вона означає, що якщо висловлення (
здійснено операцію логічного заперечення. Ця елементарна і дуже важлива у бульовій алгебрі логічна операція називається інверсією (логічним запереченням). Вона означає, що якщо висловлення ( 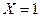 ) істинне, то висловлення "НЕ X" (
) істинне, то висловлення "НЕ X" ( 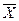 ) - хибне (
) - хибне ( 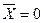 ), а якщо висловлення X - хибне (
), а якщо висловлення X - хибне ( 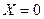 ), то висловлення
), то висловлення 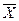 - істинне (
- істинне ( 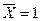 ).
).
Логічна функція 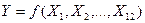 - це складне висловлення з кількох простих, які пов’язані між собою логічними операціями. Логічна функція
- це складне висловлення з кількох простих, які пов’язані між собою логічними операціями. Логічна функція 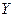 набуває значення 0 або 1 (
набуває значення 0 або 1 ( 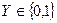 ) при наборі логічних двійкових змінних (аргументів)
) при наборі логічних двійкових змінних (аргументів) 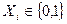 .
.
Якщо кожному значенню аргументу відповідає тільки одне значення логічної функції, така функція називається однозначною, якщо два або більше - багатозначною. Однозначна функція 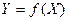 може бути зображена тільки двома аргументами (0 і 1) і двома своїми значеннями (0 і 1). Отже, число однозначних функцій у цьому випадку може бути тільки 22=4. Особливо цікава одна з них - інверсія
може бути зображена тільки двома аргументами (0 і 1) і двома своїми значеннями (0 і 1). Отже, число однозначних функцій у цьому випадку може бути тільки 22=4. Особливо цікава одна з них - інверсія 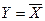 , решта - тривіальні.
, решта - тривіальні.
Вхідний набір - це певна комбінація значень двійкових змінних 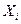 . у логічній функції У . Максимальне число вхідних наборів визначається як
. у логічній функції У . Максимальне число вхідних наборів визначається як 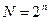 (де n - число змінних), максимальне число логічних функцій n змінних - як
(де n - число змінних), максимальне число логічних функцій n змінних - як 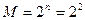 .
.
Двозначні функції 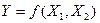 мають N=4 можливих значень аргументів /
мають N=4 можливих значень аргументів / 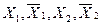 / і два різних значення функцій (
/ і два різних значення функцій ( 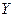 і
і 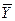 ), що в результаті дає 24=16 різних двозначних бульових функцій. Число наборів аргументів 22=4. а їх значення такі:
), що в результаті дає 24=16 різних двозначних бульових функцій. Число наборів аргументів 22=4. а їх значення такі: 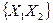 ,
, 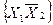 ,
, 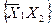 ,
, 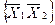 . У випадку функції трьох змінних
. У випадку функції трьох змінних 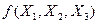 різних наборів аргументів буде
різних наборів аргументів буде
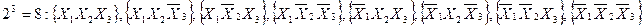 а різних значень тризначної функції буде вже 28=256.
а різних значень тризначної функції буде вже 28=256.
Логічна функція, яка має певні значення 0 або 1 на всіх вхідних наборах, називається повністю визначеною функцією. Якщо логічна функція мав значення, які на деяких вхідних наборах не визначені, їх називають байдужими (або непевними). Частково визначену логічну функцію можна зробити повністю визначеною (довизначеною) приписуванням байдужим наборам довільних значень функції.
Множину логічних Функцій 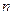 змінних можна утворити з допомогою трьох основних логічних операцій:
змінних можна утворити з допомогою трьох основних логічних операцій:
· логічного заперечення (“-”) - інверсії;
· логічного додавання (“v”) – диз’юнкції;
· логічного множення (“.”) кон’юнкції.
Для згаданих операцій справедливі такі аксіоми (тотожності або правила):
· універсальна множина –{ 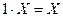 ; 1vX=1;}
; 1vX=1;}
· нульова множина -{ 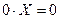 ; 0vX=X;}
; 0vX=X;}
· повторення (тавтологія) -{ 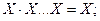 XvXv…vX=X;}
XvXv…vX=X;}
· доповнення –{Ошибка! Объект не может быть создан из кодов полей редактирования.; XvОшибка! Объект не может быть создан из кодов полей редактирования.;}
· подвійна інверсія - 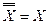 .
.
В алгебрі логіки діє принцип дуальності, згідно з яким дві функції рівносильні одна одній, якщо на всіх можливих наборах змінних вони набувають одного і того самого значення, тобто 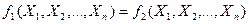 . Принцип дуальності (двоїстості) є основним принципом бульової алгебри. Він має велике практичне значення, що визначило одну з переваг цифрової техніки. Застосовуючи його, можна будувати нові логічні функції, логічні елементи та пристрої, причому досить просто. Властивість дуальності /двоїстості/ бульової функції е основою наступних двох правил бульової алгебри:
. Принцип дуальності (двоїстості) є основним принципом бульової алгебри. Він має велике практичне значення, що визначило одну з переваг цифрової техніки. Застосовуючи його, можна будувати нові логічні функції, логічні елементи та пристрої, причому досить просто. Властивість дуальності /двоїстості/ бульової функції е основою наступних двох правил бульової алгебри:
правило К. Шеннона стверджує, що для одержання алгебраїчного виразу інверсної функції необхідно у згаданій функції всі змінні замінити на інверсні їм, всі знаки кон’юнкції - на знаки диз’юнкції, а всі знаки диз’юнкції - на знаки кон’юнкції;
правило де Моргана стверджує, що інверсія кон’юнкції дорівнює диз’юнкції інверсій, а інверсія диз’юнкції – кон’юнкції інверсій.
У бульовій алгебрі також діють закони, за якими можна встановити аналітичні зв’язки між різними логічними функціями і виконувати відповідні перетворення для спрощення складних виразів. Основні закони бульової алгебри зведені в табл.1.4. Справедливість аксіом і законів легко перевірити прямою підстановкою нуля або одиниці на місце конкретного аргументу.
Таблиця 1.4 Основні закони булевої алгебри
| Закони комутативності /переміщення/ | 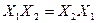
 v v 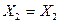 v v 
|
| Закони асоціативності /сполучення/ | 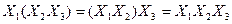
 v v 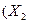 v v 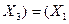 v v 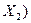 v v 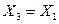 v v  v v 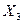
|
| Закони дистрибутивності /розподілу/ | 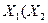 v v 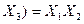 v v 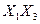
 v v 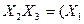 v v 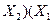 v v 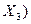
|
| Закони склеювання | 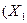 v v 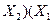 v v 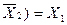
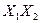 v v 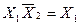
|
| Закони поглинання | 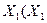 v v 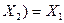
 v v 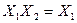
|
| Закони дуальності /правило де Моргана/ | 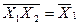 v v 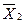
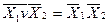
|
Застосовуючи аксіоми (тотожності) та закони бульової алгебри, можна отримати нові логічні формули, а також довести справедливість того чи іншого закону на основі інших.
Особливої уваги заслуговують закони дуальності (правило де Моргана), з допомогою яких кон’юнкцію можна виразити через диз’юнкцію, і навпаки. Таку операцію часто треба здійснювати при перетвореннях Логічних виразів. Корисними для практики можуть бути також наслідки законів дуальності, зокрема:
 v
v 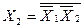 ; ( 1.2)
; ( 1.2)
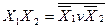 ; ( 1.3)
; ( 1.3)
Закони дуальності та наслідки з них справедливі для довільного числа змінних:
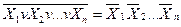 ;
; 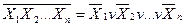 ;
;
1.5 Властивості логічних функцій
Властивості логічних функцій розглянемо на прикладі двозначної логічної функції 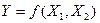 яка на практиці зустрічається найчастіше. Для цього складемо табл. 1.5 всіх можливих наборів аргументів у вигляді двійкових чисел: 00, 01, 10, 11; всі 16 значень функції розміщено у порядку зростання двійкових чисел (від 0000 до 1111).
яка на практиці зустрічається найчастіше. Для цього складемо табл. 1.5 всіх можливих наборів аргументів у вигляді двійкових чисел: 00, 01, 10, 11; всі 16 значень функції розміщено у порядку зростання двійкових чисел (від 0000 до 1111).
Таблиця 1.5 Двозначні логічні функції
| Фун-кція | Набір аргументів | Назва логічної функції | Визначення логічної Функції | |||
| 0 0 | 0 1 | 1 0 | 1 1 | |||
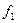
| 0 | 0 | 0 | 0 | Константа нуль | 0 |
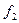
| 0 | 0 | 0 | 1 | Кон’юнкція | 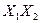
|
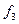
| 0 | 0 | 1 | 0 | Заборона 
| 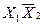
|
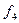
| 0 | 0 | 1 | 1 | Повторення 
| 
|
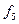
| 0 | 1 | 0 | 0 | Заборона 
| 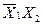
|
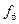
| 0 | 1 | 0 | 1 | Повторення 
| 
|
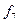
| 0 | 1 | 1 | 0 | Виняткове АБО |  Å Å 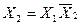 v v 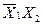
|
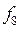
| 0 | 1 | 1 | 1 | Диз’юнкція |  v v 
|
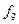
| 1 | 0 | 0 | 0 | Функція Пірсона | 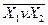
|
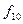
| 1 | 0 | 0 | 1 | Рівнозначність |  ~ ~ 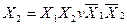
|
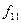
| 1 | 0 | 1 | 0 | Інверсія 
| 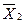
|
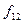
| 1 | 0 | 1 | 1 | Імплікація від  до до 
| 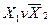
|
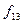
| 1 | 1 | 0 | 0 | Інверсія 
| 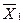
|
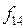
| 1 | 1 | 0 | 1 | Імплікація від  до до 
| 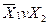
|
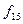
| 1 | 1 | 1 | 0 | Функція Шефера | 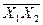
|
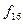
| 1 | 1 | 1 | 1 | Константа одиниця | 1 |
Всі наведені 16 логічних Функцій на практиці не застосовуються, бо, як видно з табл. 1.5, яка, до речі, має симетрію, функції 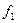 і
і 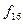 тривіальні,
тривіальні, 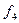 ,
, 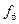 ,
, 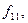
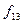 - не залежать від одного з аргументів. Хоча решта десять функцій залежать від двох аргументів, однак і серед них е такі, які можна одержати через інші.
- не залежать від одного з аргументів. Хоча решта десять функцій залежать від двох аргументів, однак і серед них е такі, які можна одержати через інші.
Аналогічно арифметичним операціям у бульовій алгебрі також існує поняття "першості виконання" операції, що визначає, яка з логічних операцій має виконуватися раніше. Отже, для логічних операцій першість визначається у такій послідовності: 1 - заперечення, 2 –кон’юнкція, 3 – диз’юнкція, 4 - імплікація, 5 - рівнозначність. При наявності у виразі логічної функції круглих дужок ступінь першості збільшується на одиницю.
Зауважимо, що деякі з наведених у табл. 1.5 функцій одержують методом перенумерації (перейменування або декомпозиції) аргументів логічних функцій. Наприклад, функція 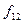 отримується з функції
отримується з функції 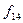 , якщо
, якщо  перенумерувати на
перенумерувати на  і навпаки, беручи набір аргументів справа наліво або зліва направо. Функцію
і навпаки, беручи набір аргументів справа наліво або зліва направо. Функцію 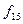 можна отримати з функції
можна отримати з функції 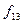 підстановкою замість
підстановкою замість  іншою функції
іншою функції 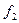 (тобто проінвертувавши набір аргументів). Така операція називається суперпозицією. Отже, застосовуючи метод суперпозицій, можна одержати більш складні логічні функції. При цьому виникає питання, чи можливий набір більш простих функцій, за допомогою яких можна було б отримати як завгодно складну логічну функцію. З практичної точки зору це дуже важливе питання, бо воно стосується технології виготовлення мікросхем і т. ін. З теоретичної точки зору воно пов’язане з основним поняттям бульової алгебри - функціональною повнотою системи логічних функцій.
(тобто проінвертувавши набір аргументів). Така операція називається суперпозицією. Отже, застосовуючи метод суперпозицій, можна одержати більш складні логічні функції. При цьому виникає питання, чи можливий набір більш простих функцій, за допомогою яких можна було б отримати як завгодно складну логічну функцію. З практичної точки зору це дуже важливе питання, бо воно стосується технології виготовлення мікросхем і т. ін. З теоретичної точки зору воно пов’язане з основним поняттям бульової алгебри - функціональною повнотою системи логічних функцій.
Набір (система) бульових функцій вважається функціонально повним. якщо на його основі або на базисі можна отримати довільну бульову Функцію, застосовуючи лише метод суперпозиції.
Функціонально повних наборів-базисів можна отримати досить багато. Найбільш поширені серед них наведені в табл. 1.6.
Найпростішим /елементарним/ базисом, що є основою бульової алгебри, е набір трьох основних логічних функцій (або операцій): 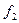 і
і 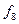 ,
, 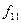 або
або 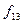 , на яких зупинимося більш детальніше (табл. 1.5, 1.6):
, на яких зупинимося більш детальніше (табл. 1.5, 1.6):
інверсія - логічне заперечення або функція НЕ; ця функція згадувалася раніше як однозначна, а тепер розглядається як двозначна ( 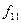 і
і 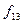 ), хоча залежить тільки від одної з двох змінних,
), хоча залежить тільки від одної з двох змінних,
диз’юнкція - логічне додавання або функція АБО, яка істинна тоді, коли істинні або  , або
, або  , або обидві змінні;
, або обидві змінні;
кон’юнкція - логічне множення або функція І, яка істинна тільки тоді, коли і  і
і  істинні.
істинні.
До більш спрощених базисів, з допомогою яких можна побудувати будь-яку складну цифрову систему обробки інформації, належить, наприклад, набір з двох елементарних логічних функцій 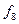 і
і 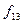 або
або 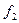 і
і 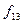 і навіть набір лише з одної логічної функції
і навіть набір лише з одної логічної функції 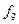 або
або 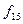 . Решту логічних функцій, які відсутні у цих базисах, можна одержати на основі правил (законів) алгебри логіки.
. Решту логічних функцій, які відсутні у цих базисах, можна одержати на основі правил (законів) алгебри логіки.
Елементи, що реалізують бульові (логічні) операції, називаються логічними елементами (ЛЕ). Якщо логічні операції і прийнято зображати у вигляді формул, то ЛЕ - графічно у вигляді схем. Умовне графічне позначення ЛЕ прийнято зображати прямокутником, у якого лінії зліва - входи аргументів 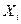 , справа –функція
, справа –функція 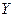 . Тип логічної операції задається спеціальною позначкою: інверсія – кружком на вході або виході (ЛЕ - інвертор), диз’юнкція - 1, кон’юнкція - & (табл. 1.6).
. Тип логічної операції задається спеціальною позначкою: інверсія – кружком на вході або виході (ЛЕ - інвертор), диз’юнкція - 1, кон’юнкція - & (табл. 1.6).
Таблиця 1.6 Основні логічні функції.
| Вхідні змінні | Диз’юн-кція АБО:
| Кон’нкція І:
| Штрих Шефера І-НЕ:
| Стрілка Пірса АБО-НЕ
| Вийняткове АБО:
| Вийняткове АБО-НЕ
| |

| 
| ||||||
| 0 0 1 1 | 0 1 0 1 | 0 1 1 1 | 0 0 0 1 | 1 1 1 0 | 1 0 0 0 | 0 1 1 0 | 1 0 0 1 |
| Назва і умовне /схемне/ позна- чення | Диз’юн-
ктор
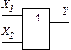
| Кон’юн-ктор 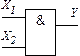
| Елемент
Шефера 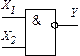
| Елемент
Пірса 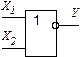
| Суматор
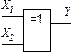
| Суматор інвертор 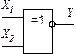
| |
Логічні функції багатьох змінних одержують аналогічно розглянутому випадку 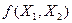 застосуванням методу суперпозиції та аксіом і законів алгебри логіки. Слід зауважити, що базисні функції обов'язково містять у собі операцію інверсії. Побудовані на їх основі логічні елементи (наприклад, на елементах Шефера або Пірса) дозволяють будувати функціональні вузли цифрових систем будь-якої складності.
застосуванням методу суперпозиції та аксіом і законів алгебри логіки. Слід зауважити, що базисні функції обов'язково містять у собі операцію інверсії. Побудовані на їх основі логічні елементи (наприклад, на елементах Шефера або Пірса) дозволяють будувати функціональні вузли цифрових систем будь-якої складності.
Особливий інтерес для практики має функція 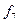 сума за модулем 2, яку ще називають “виняткове АБО". Логічний елемент-суматор за модулем 2, що реалізує цю функцію, широко застосовують у різних цифрових функціональних пристроях комбінаційного типу.
сума за модулем 2, яку ще називають “виняткове АБО". Логічний елемент-суматор за модулем 2, що реалізує цю функцію, широко застосовують у різних цифрових функціональних пристроях комбінаційного типу.
Особливість функції “виключне АБО” в тому, що вона збігається з функцією АБО в усіх випадках, за винятком, одного, коли всі змінні набувають значення одиниці, а саме при 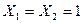 . 3 цієї причини, очевидно, ця функція й називається "виняткове АВО” Символ Å псевдоплюс означає, що змінні (аргументи)
. 3 цієї причини, очевидно, ця функція й називається "виняткове АВО” Символ Å псевдоплюс означає, що змінні (аргументи)  і
і  пов’язані логічною функцією “вийняткове АБО” яка істинна тоді, коли одна із змінних (
пов’язані логічною функцією “вийняткове АБО” яка істинна тоді, коли одна із змінних (  або
або  ) є істинною:
) є істинною:
 Å
Å 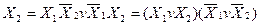
Виняткове АБО (цю функцію ще називають нерівнозначністю або нееквівалентністю) має властивості:
комутативності  Å
Å  =
=  Å
Å  ;
;
асоціативності  Å
Å 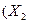 Å
Å 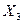 )=(
)=(  Å
Å  )Å
)Å 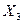 ;
;
дистрибутивності відносно кон’юнкції 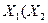 Å
Å 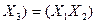 Å
Å 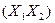 .
.
Справедливі також аксіоми 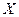 Å 0
Å 0 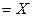 ;
; 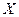 Å
Å 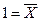 ;
; 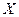 Å
Å 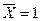 ;
; 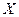 Å
Å 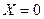 .
.
На основі властивостей і аксіом функції ''вийняткове АВО” можна одержати функцію елементарного базису:
НЕ - 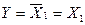 Å 1; І -
Å 1; І - 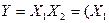 Å
Å 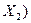 Å
Å 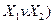 ;
;
АБО - 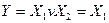 Å
Å  Å
Å 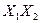
Для функції “вийняткове АБО-НЕ” (рівнозначність або еквівалентність) справедлива така рівність:
 ~
~ 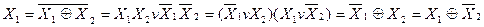
1.6 Форми зображення логічних функцій
Будь-яку логічну функцію можна задати або зобразити у різних формах: словесно, таблично, числового запису, аналітичне і координатної карти чи діаграми. Розглянемо кожну з цих форм окремо.
Словесне зображення - це логічне висловлення, під яким розуміють довільне твердження, щодо якого можна сказати, істинне воно або хибне. Наприклад, функцію 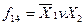 - імплікацію від
- імплікацію від  до
до 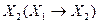 словесно можна зобразити (описати) так (див. табл. 1.5): функція
словесно можна зобразити (описати) так (див. табл. 1.5): функція 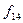 хибна тоді і тільки тоді, коли
хибна тоді і тільки тоді, коли  істинне і
істинне і  хибне.
хибне.
Табличне зображення характеризується таблицею істинності, яка має 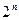 рядків за числом вхідних наборів,
рядків за числом вхідних наборів, 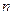 - стовпців за числом змінних
- стовпців за числом змінних 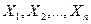 т - стовпців за числом функцій (
т - стовпців за числом функцій ( 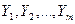 ).У випадку однозначної функції число стовпців таблиці істинності дорівнює n+ 1, а для багатозначної функції n+ т. Приклад однозначної функції трьох змінних
).У випадку однозначної функції число стовпців таблиці істинності дорівнює n+ 1, а для багатозначної функції n+ т. Приклад однозначної функції трьох змінних 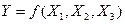 , яку зображено таблицею істинності, наведеної у табл. 1.7. Функцію, зображену таблицею істинності, можна також "читати" аналогічно, як при словесному зображенні.
, яку зображено таблицею істинності, наведеної у табл. 1.7. Функцію, зображену таблицею істинності, можна також "читати" аналогічно, як при словесному зображенні.
Таблиця 1.7 Таблично задана логічна функція
| Номер набору |  
| 
| 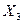
| 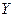
|
| 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 |
| 3 | 0 | 1 | 1 | 1 |
| 4 | 1 | 0 | 0 | 1 |
| 5 | 1 | 0 | 1 | 0 |
| 6 | 1 | 1 | 0 | 0 |
| 7 | 1 | 1 | 1 | 1 |
Кожний спосіб чи форма зображення має свою специфіку і тому буде зручною там, де даний спосіб є найбільш простим чи компактним. Таблична форма запису хоча й наочна і може бути застосована для довільного числа змінних, однак при аналізі властивостей функції такий запис не є компактним. Для випадку чотирьох і більше змінних табличне зображення логічної функції е суттєво складнішим та громіздким. Простішим буде числовий запис, коли логічна функція задається у вигляді послідовності десяткових чисел, що є еквівалентами тих вхідних наборів, на яких дана функція набуває значення 1 або 0. Наприклад, таблицю істинності (табл. 1.7) легко переписати у числову, форму: для вхідних наборів, на яких 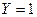 . маємо
. маємо 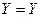 (0,3,4,7), а для наборів, на яких
(0,3,4,7), а для наборів, на яких 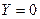 , маємо
, маємо 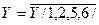 або для
або для 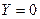 маємо
маємо 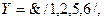 а для
а для 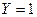
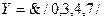 , де кожний з записів повністю зображує логічну функцію, подану табл. 1.7, і, як бачимо, а більш компактним.
, де кожний з записів повністю зображує логічну функцію, подану табл. 1.7, і, як бачимо, а більш компактним.
При аналітичному зображенні функція задається алгебраїчним виразом, який отримують при застосуванні логічних операцій до змінних бульової алгебри. Якщо попередні форми зображення логічної функції лише вказують значення функції на конкретних наборах змінних, то аналітичне зображення, крім того, ще дозволяє виконувати різні аналітичні перетворення, які необхідні як для аналізу, так і для синтезу цифрового пристрою, що реалізує або має реалізувати дану логічну функцію.
Нехай на фіксованому вхідному наборі { 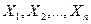 } задана логічна функція
} задана логічна функція 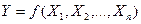 . Оскільки кожна змінна
. Оскільки кожна змінна 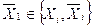 =
= 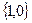 ,набір значень змінних, очевидно, є конкретним двійковим числом
,набір значень змінних, очевидно, є конкретним двійковим числом 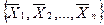 . За номер вхідного набору можна взяти довільне число
. За номер вхідного набору можна взяти довільне число
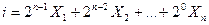
В інших випадках, наприклад, коли набір 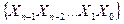 зображує двійкове число, більш зручним є запис номера набору як:
зображує двійкове число, більш зручним є запис номера набору як:
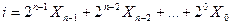
Найбільш раціональним е зображення логічних функцій в так званих нормальних (канонічних) формах запису, зокрема, у вигляді диз’юнкції кон’юнкцій або кон’юнкції диз’юнкцій змінних, що взяті з інверсіями або без них. Окремі вирази функції змінних 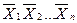 називають термами, а самі (однозначні) функції
називають термами, а самі (однозначні) функції 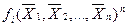 -конституентами.
-конституентами.
Кон’юнктивний терм (мінтерм або конституента одиниці) 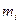 - це терм, що зв’язує всі змінні, які зображені у прямій або у інверсній формі знаком кон’юнкції, причому
- це терм, що зв’язує всі змінні, які зображені у прямій або у інверсній формі знаком кон’юнкції, причому
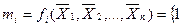 , якщо номер набору дорівнює
, якщо номер набору дорівнює 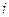 ;
;
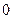 , якщо номер набору не дорівнює
, якщо номер набору не дорівнює 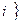 ;
;
Наприклад: 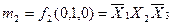
Або 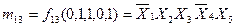
Диз’юнктивний терм (макстерм або конституента нуля) 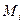 - це терм, що зв’язує всі змінні, які зображені у прямій або у інверсній формі знаком диз’юнкції, причому
- це терм, що зв’язує всі змінні, які зображені у прямій або у інверсній формі знаком диз’юнкції, причому
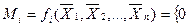 ,якщо номер набору дорівнює
,якщо номер набору дорівнює 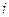 ;
;
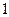 , якщо номер набору не дорівнює
, якщо номер набору не дорівнює 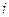 ;
;
Наприклад: 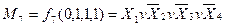
Або 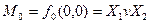
Ранг терма 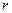 визначається кількістю змінних, які входять у даний терм. Наприклад, мінтерм
визначається кількістю змінних, які входять у даний терм. Наприклад, мінтерм 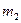 має
має 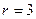 , а
, а 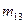 має
має 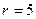 , макстерм
, макстерм 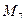 має
має 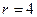 , а
, а 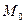 має
має 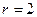 .
.
Згідно із законом дуальності будь-яку логічну функцію 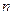 змінних можна зобразити як диз’юнкцію кон’юнкцій (мінтерм) або як кон’юнкцію диз’юнкцій (макстерм) змінних. Однозначне зображення логічних функцій одержують тільки при так званих удосконалених нормальних формах (УНФ), тобто таких, при яких мінтерми або макстерми формуються з усіх аргументів логічної функції і є одного (причому максимального) рангу. Якщо логічна функція складається з набору диз’юнкцій елементарних кон’юнкцій одного рангу, її називають удосконаленою диз’юнктивно-нормальною формою (УДНФ), а якщо з набору кон’юнкцій елементарних диз’юнкцій - удосконаленою кон’юнктивно-нормальною формою (УКНФ) зображення. Для
змінних можна зобразити як диз’юнкцію кон’юнкцій (мінтерм) або як кон’юнкцію диз’юнкцій (макстерм) змінних. Однозначне зображення логічних функцій одержують тільки при так званих удосконалених нормальних формах (УНФ), тобто таких, при яких мінтерми або макстерми формуються з усіх аргументів логічної функції і є одного (причому максимального) рангу. Якщо логічна функція складається з набору диз’юнкцій елементарних кон’юнкцій одного рангу, її називають удосконаленою диз’юнктивно-нормальною формою (УДНФ), а якщо з набору кон’юнкцій елементарних диз’юнкцій - удосконаленою кон’юнктивно-нормальною формою (УКНФ) зображення. Для 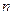 -змінних складається
-змінних складається 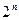 мінтерм
мінтерм 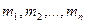 (при УДНФ) або
(при УДНФ) або 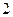 макстерм
макстерм 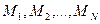 (при УКНФ).
(при УКНФ).
В загальному випадку алгебраїчний вираз логічної функції в УДНФ
набував вигляду
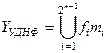 (1.5)
(1.5)
де 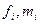 - значення функції (0або 1) та мінтерма на
- значення функції (0або 1) та мінтерма на 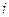 -му наборі змінних.
-му наборі змінних.
В УКНФ загальний вираз логічної функції
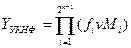 (1.6)
(1.6)
де 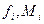 - значення функції (0 або 1) та макстерма на
- значення функції (0 або 1) та макстерма на 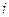 -му наборі змінних.
-му наборі змінних.
Застосовуючи закони алгебри логіки (див. табл.1.4), неважко довести еквівалентність обох форм зображення будь-якої логічної функції. Такі форми зображення логічних функцій необхідні при проектуванні цифрових пристроїв.
Для згаданого прикладу (див. табл.1.7) можна записати два тотожних (дуальних) вирази логічної функції. Беручи лише до уваги конституенти 1, маємо
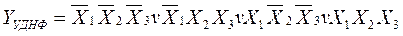
а для конституент 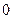
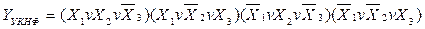
Отже, якщо логічну функцію задано таблично, то для переходу до її аналітичного зображення в УНФ роблять так:
для зображення в УДНФ описують ті набори змінних, для яких . функція дорівнює одиниці, тобто для конституент І; для кожного такого набору складають мінтерм, причому змінні 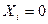 замінюють на
замінюють на 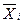 і одержані мінтерми з’єднують диз'юнкціею;
і одержані мінтерми з’єднують диз'юнкціею;
для зображення в УКНФ виписують набори, для яких функція дорівнює нулю, тобто для констатуент 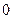 для кожного набору складають макстерм, причому змінні
для кожного набору складають макстерм, причому змінні 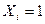 замінюють на
замінюють на 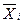 і одержані макстерми об’єднують кон'юнкцією.
і одержані макстерми об’єднують кон'юнкцією.
Приклад: Утворити УДНФ логічної функції, що задана в ДНФ:
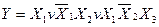
Розв’язання. Для підвищення рангу кон’юнкції молодшого рангу застосовуємо доповнення типу 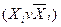 :
:
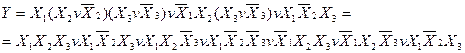
Приклад: Таблично-задану логічну функцію 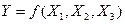 записати в аналітичній формі (див.табл. 1.8) для тотожних зображень УДНФ та УКНФ.
записати в аналітичній формі (див.табл. 1.8) для тотожних зображень УДНФ та УКНФ.
Розв’язання. В УДНФ:
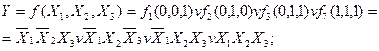
В УКНФ:
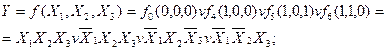
Таблиця 1.8 Таблично задана логічна функція.
| Номер набору | 
| 
| 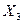
| 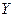
|
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 |
| 2 | 0 | 1 | 0 | 1 |
| 3 | 0 | 1 | 1 | 1 |
| 4 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 |
| 6 | 1 | 1 | 0 | 0 |
| 7 | 1 | 1 | 1 | 1 |
Слід зауважити, що в даному прикладі вибір форми зображення логічної функції не має принципового значення, бо число мінтерм дорівнює числу макстерм. Проте у випадках, коли число одних переважав над числом інших, наприклад, кількість 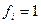 більша за кількість
більша за кількість 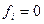 , або навпаки, тоді менш громіздким буде функція з меншим числом терм.
, або навпаки, тоді менш громіздким буде функція з меншим числом терм.
Приклад: Перейти до УКНФ логічної функції, що задана в УДНФ
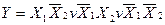
Розв’язання. Спочатку спростимо вираз за законом склеювання:
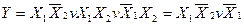
Застосувавши правило Шеннона, маємо
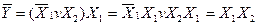
За принципом подвійної інверсії та законом дуальності остаточно одержимо
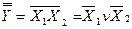
1.7 Мінімізація логічних функцій
Зведення логічної функції до УДНФ або до УКНФ дає однозначне зображення 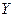 . Однак для технічної реалізації такої логічної функції властивість однозначності зображення буде зручним тільки в тому випадку, якщо повним набором логічних елементів є елементарний базис, що складається з окремих елементів І, АБО, НЕ, причому з числом входів елементів І та АБО, що дорівнює рангу термів логічної функції. На практиці часто доводиться будувати цифрові пристрої на різних базисах, і тоді з’ясовується, що удосконалені форми зображення логічних функцій не завжди найекономніші. Їм властива надлишковість, яка підлягає спрощенню, тобто мінімізації. Цій процедурі, до речі, можуть підлягати логічні функції інших, не обов’язково удосконалених, форм зображення.
. Однак для технічної реалізації такої логічної функції властивість однозначності зображення буде зручним тільки в тому випадку, якщо повним набором логічних елементів є елементарний базис, що складається з окремих елементів І, АБО, НЕ, причому з числом входів елементів І та АБО, що дорівнює рангу термів логічної функції. На практиці часто доводиться будувати цифрові пристрої на різних базисах, і тоді з’ясовується, що удосконалені форми зображення логічних функцій не завжди найекономніші. Їм властива надлишковість, яка підлягає спрощенню, тобто мінімізації. Цій процедурі, до речі, можуть підлягати логічні функції інших, не обов’язково удосконалених, форм зображення.
Мінімізація - це процес зведення логічної функції до такого виду, який припускає більш просту і дешеву її фізичну реалізацію, тобто з меншим числом логічних елементів за рахунок зменшення числа логічних символів, кількості змінних та зв’язків між елементами.
Відомо кілька методів мінімізації, серед яких найбільш поширеними в інженерній практиці є такі:
· безпосередніх перетворень;
· карт Карно;
· Квайна.
Знайти гарантовано мінімальний вираз для довільної логічної функції можна лише методом повного перебору в процесі мінімізації всіх можливих варіантів. Від руки (на папері) це реально здійснити для невеликої кількості змінних. Із збільшенням числа змінних складність розглянутих методів мінімізації зростає за геометричною прогресією і стає під силу лише автоматизованим методам, які призначені для ЕОМ.
Для оцінки складності логічної функції, яка зображена тою чи іншою формою, вводиться поняття ціни реалізації (покриття) логічної функції. За Квайном ціна покриття логічної функції визначається числом змінних (букв) в конституенті, що рівнозначно числу входів логічних елементів, які реалізують задану функцію. Кон’юнкціі вищого рангу покриваються відповідними кон’юнкціями нижчого рангу. Наприклад, кон’юнкції 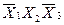 і
і 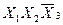 покриваються кон’юнкціею
покриваються кон’юнкціею 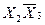 .
.
В загальному випадку операцію покриття зображає операція склеювання (див. табл.1.3) 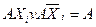 , де
, де 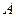 - елементарна кон’юнкція або імпліканта. тобто така логічна функція, яка отримана в результаті склеювання і яка на будь-якому наборі змінних
- елементарна кон’юнкція або імпліканта. тобто така логічна функція, яка отримана в результаті склеювання і яка на будь-якому наборі змінних 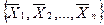 набуває такого самого значення, що й сама функція (конституента), що її утворила. Чим. більше число покриттів, що знижують ранг імпліканти, тим простіший кінцевий вираз. Прості імпліканти – це елементарні кон’юнкції (що мають менше число членів, ніж змінних) найнижчого рангу, які входять у дану логічну функцію. Якщо в днз’юнкції простих імплікант жодну з них шляхом поглинання вилучити (покрити) не вдається, таку диз’юнкцію називають тупиковою, або мінімізованою диз’юнктивно-нормальною формою (МДНФ) заданої функції.
набуває такого самого значення, що й сама функція (конституента), що її утворила. Чим. більше число покриттів, що знижують ранг імпліканти, тим простіший кінцевий вираз. Прості імпліканти – це елементарні кон’юнкції (що мають менше число членів, ніж змінних) найнижчого рангу, які входять у дану логічну функцію. Якщо в днз’юнкції простих імплікант жодну з них шляхом поглинання вилучити (покрити) не вдається, таку диз’юнкцію називають тупиковою, або мінімізованою диз’юнктивно-нормальною формою (МДНФ) заданої функції.
Таким чином, загальною задачею мінімізації логічних функцій є знаходження скороченої ДНФ, тобто знаходження всіх простих імплікант, визначення серед них тупикових ДНФ і, нарешті, вибір з останніх мінімальних, які утворюють МДНФ заданої логічної функції.
Метод безпосередніх перетворень - це аналітичний метод спрощення логічних функцій з допомогою аксіом та законів бульової алгебри (див. табл.1.4). При набутті певних навичок цей метод є досить ефективним для малої кількості змінних (як правило, не більше трьох).
Для мінімізації логічних функцій методом безпосередніх перетворень корисно використовувати такі формули бульової алгебри:
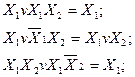
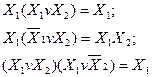
У деяких випадках ефективніше мінімізувати інверсію логічної функції для отримання простішого виразу в МДНФ. Це може бути тоді, коли логічна функція має переважаюче число одиниць, ніж нулів. Тоді, маючи МДНФ інверсної функції, при технічній реалізації цієї функції достатньо на виході побудованої схеми під’єднати інвертор для відновлення прямої функції.
Приклад: Отримати МДНФ для логічної функції, що задана таблицею істинності (див. табл. 1.9).
Таблиця 1.9 Таблично задана логічна функція

| 
| 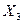
| 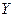
|
| 0 0 0 0 1 1 1 1 | 0 0 1 1 0 0 1 1 | 0 1 0 1 0 1 0 1 | 1 1 0 1 1 1 0 1 |
Розв’язання. Оскільки у даній функції число одиниць переважає над числом нулів, виконаємо мінімізацію для її інверсії:
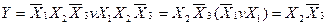
Отже, 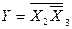 . Порівняємо з МДНФ прямої функції:
. Порівняємо з МДНФ прямої функції:
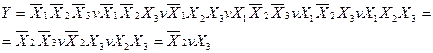
Приклад : Методом безпосередніх перетворень мінімізувати логічну функцію
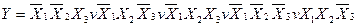
Розв’язання:
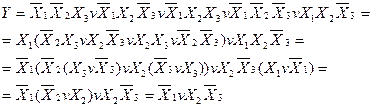
1.8 Структурна реалізація логічних функцій
Наступним кроком після мінімізації логічної функції є побудова її структурної схеми. Цей етап проектування належить до структурного синтезу цифрового пристрою. Початковими даними для виконання структурного синтезу логічної схеми автомата є, як правило, МДНФ або МКНФ логічної функції, а для багатозначної функції - система логічних Функцій, що зображені у МДНФ або у МКНФ.
Задачу структурної реалізації логічної функції (або функцій) сформулюємо так: для заданих вхідних змінних 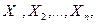 на наборах яких визначена (або частково визначена) логічна функція, що зображена у МДМФ або у МКНФ, побудувати структурну логічну схему, яка б реалізувала цю функцію у заданому базисі.
на наборах яких визначена (або частково визначена) логічна функція, що зображена у МДМФ або у МКНФ, побудувати структурну логічну схему, яка б реалізувала цю функцію у заданому базисі.
За основний критерій при цьому беремо мінімум апаратурних затрат, під яким слід розуміти мінімальну кількість ЛЕ та мінімальне число зв’язків між ними.
Визначальну роль у забезпеченні критерію за мінімумом апаратурних затрат відіграє елементний базис, тобто певний набір функціонально повних ЛЕ, на яких можна реалізувати довільну логічну функцію. Якщо базис наперед не заданий, то при такому абстрактному синтезі жодних перетворень із заданою логічною функцією робити не потрібно, досить лише структурно реалізувати за допомогою ЛЕ всі її логічні операції.
Однак, якщо базис за умовою завдання наперед заданий, дану логічну функцію необхідно спеціально перетворити. Головна мета цих перетворень - зведення виразу функції до заданого базису. Раціональність і ефективність такого підходу забезпечує швидку побудову структурної логічної схеми синтезованого цифрового пристрою. Наприклад, якщо задамо базис 2І-НЕ (елемент Шефера) або 2АБО-НЕ (елемент Пірса), для реалізації функції змінних відповідними перетвореннями і замінами МДНФ або МКНФ цієї функції мають бути зображені у вигляді 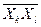 або
або 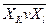 . Очевидно, що при заданому базисі 2І-АБО-НЕ логічна функція має набувати такого остаточного вигляду:
. Очевидно, що при заданому базисі 2І-АБО-НЕ логічна функція має набувати такого остаточного вигляду: 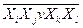 .
.
При виконанні структурного синтезу цифрового пристрою доцільно користуватися розкладанням логічної функції за принципом, що нагадує дерево, коріння якого вихід (або виходи), а гілки - входи змінних.
Нехай, наприклад, у базисі елемента Шефера потрібно реалізувати логічну функцію
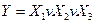
Оскільки елемент Шефера - це 2І-НЕ, в даній функції необхідно зробити такі перетворення, в яких у явному вигляді проявляться ознаки функції 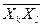 . Для одержання виразу даної функції у заданому базисі потрібно застосувати подвійну інверсію та закон дуальності (правило де Моргана):
. Для одержання виразу даної функції у заданому базисі потрібно застосувати подвійну інверсію та закон дуальності (правило де Моргана):
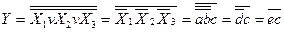
Отже, для реалізації даної функції у базисі елемента Шефера потрібно 4 ЛЕ НЕ і 2 ЛЕ 2І-НЕ. Інвертор легко реалізується на 2І-НЕ. якщо його входи з’єднати (при 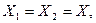
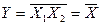 ) або якщо до одного з входів прикласти високий рівень (наприклад, при
) або якщо до одного з входів прикласти високий рівень (наприклад, при 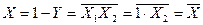 ). Схему, що реалізує диз’юнкцію трьох змінних на елементах Шефера, показано на рис. 1.1.
). Схему, що реалізує диз’юнкцію трьох змінних на елементах Шефера, показано на рис. 1.1.
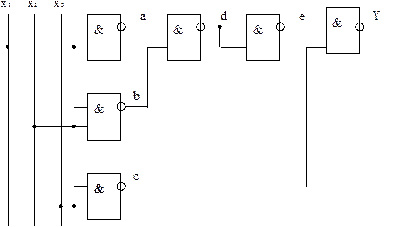
Рис. 1.1 Диз’юнкція трьох змінних в базисі 2І-НЕ
Якщо елементи Шефера замінити елементами Пірса, то згідно з принципом дуальності така логічна схема буде реалізувати кон’юнкцію трьох змінних.
1.9 Загальні відомості про цифрові автомати
Вичерпне визначення поняття "цифровий автомат" дав автор цього терміну В.М.Глушков[[i]]: "Електронні цифрові машини з програмним керуванням являють собою приклад одного з найпоширеніших сьогодні типів перетворювачів дискретної інформації, названих дискретними або цифровими автоматами. Тому задача синтезу схем електронних цифрових машин з програмним керуванням входить як частковий випадок в більш загальну задачу синтезу схем цифрових автоматів". Отже, будь-який елемент, вузол, пристрій чи навіть ЕОМ, незалежно від складності їх функціонування, є перетворювачами цифрової інформації – цифровими автоматами.
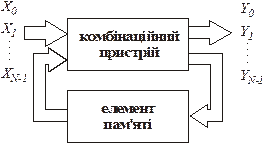
У загальному випадку на вхід цифрового автомата надходить множина двійкових змінних X0, X1, … XN-1, а з виходу знімається множина двійкових функцій Y0, Y1, … YN-1. Відмінна особливість цифрових автоматів полягає в тому, що цей функціональний зв'язок визначається також дискретною множиною внутрішніх станів, причому перехід з одного стану в інший здійснюється стрибкоподібно. Реальні цифрові автомати можуть мати лише скінченну множину внутрішніх станів, а тому - скінченне число станів, входів та виходів. Через це цифрові автомати називають ще скінченними.
Вихідні сигнали цифрового автомата залежать як від вхідних сигналів, що діють у даний (фіксований) момент часу, так і від передісторії, тобто від тих сигналів, які надійшли на його входи раніше і зафіксувались в елементах пам’яті – запам’ятовувачах Отже, роботу автомата слід розглядати щодо конкретного інтервалу часу T -такту. Такт - це скінченний відрізок часу, який необхідний для передачі одного з розрядів двійкового числа /біта/ - у разі послідовного коду, або всього двійкового коду (слова) одночасно - при паралельному коді. Залежно від того, чим визначається такт Т , розрізняють асинхронні та синхронні автомати. В асинхронних цифрових автоматах Т ¹ cоnst і зміна вхідних сигналів зразу викликає певну зміну вихідних сигналів, у синхронних Т=const і тому зміна вхідних сигналів викликає певну зміну вихідних тільки після подачі синхронізуючих (тактових) імпульсів, які керують роботою автомата.
Для опису законів функціонування цифрових автоматів зручно користуватись абстрактним часом, що набуває цілих невід’ємних значень (t=0,1,2,...), а не тактом Т. Наприклад, позначимо такти роботи автомата як t і t + 1 . Алгебраїчний вираз, який розкриває функціональний зв’язок цифрового автомата між вихідним сигналом у такті t + 1 і множиною вхідних сигналів та станів у попередньому такті t називається функцією переходу d.
Найпростішою математичною моделлю цифрового автомата з одним входом X і одним виходом є абстрактний автомат, що заданий сукупністю таких величин:
скінченою множиною вхідних сигналів (вхідний алфавіт) автомата
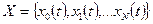 ;
;
скінченою множиною вихідних сигналів /вихідний алфавіт/ автомата
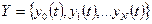 ;
;
довільною множиною станів /алфавіт станів/ автомата
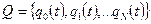
а також початковим станом автомата 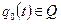 , функцією переходу автомата з одного стану в інший
, функцією переходу автомата з одного стану в інший 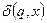 та функцією виходу автомата
та функцією виходу автомата 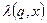 .
.
1.10 Різновиди цифрових автоматів та особливості їх функціонування
У теорії автоматів найповніше описані синхронні (цифрові) автомати. Закон функціонування будь-якого абстрактного синхронного автомата визначається його вихідним сигналом 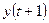 , який залежить від вхідних сигналів
, який залежить від вхідних сигналів 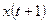 та від внутрішніх станів (чи стану)
та від внутрішніх станів (чи стану) 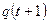 і/або
і/або 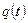 автомата. Тому існують дві можливості визначення реакції вихідного сигналу на ці дії:
автомата. Тому існують дві можливості визначення реакції вихідного сигналу на ці дії:
1) коли 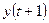 однозначно залежить від вхідного сигналу
однозначно залежить від вхідного сигналу 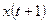 і попереднього стану
і попереднього стану 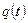 , такий автомат описується системою функцій переходу і виходу
, такий автомат описується системою функцій переходу і виходу
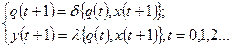 ( 1.4)
( 1.4)
і називається автоматом 1-го роду;
2) коли 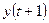 однозначно залежить від вхідного сигналу
однозначно залежить від вхідного сигналу 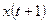 і стану
і стану 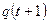 у даний момент часу -
у даний момент часу -
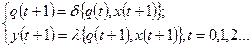 ( 1.5)
( 1.5)
це автомат 2-го роду.
Цифрові автомати 1-го роду, що функціонують за законом (1.4), називаються автоматами Мілі (Mealy). а частковий випадок автоматів 2-го роду, для яких вихідні сигнали залежать тільки від стану 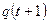 автомата і не залежать від значень вхідних сигналів, називають автоматами Мура (Мооrе). Для них закон функціонування буде заданий частковим випадком системи рівнянь автоматів 2-го роду, а саме
автомата і не залежать від значень вхідних сигналів, називають автоматами Мура (Мооrе). Для них закон функціонування буде заданий частковим випадком системи рівнянь автоматів 2-го роду, а саме
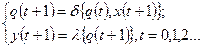
Отже, на відміну від автомата Мілі вихідний сигнал у автоматі Мура залежить тільки від біжучого стану автомата і в явному виді не залежить від вхідного сигналу. Автомати Мура і Мілі взаємозамінні – існують прості способи еквівалентного переходу від одного до іншого.
Довільний абстрактний цифровий автомат Мілі або Мура називають ще автоматом з пам'яттю, тобто таким, що здатний запам'ятовувати попередню інформацію, якщо він мав число внутрішніх станів більше за один. Якщо цифровий автомат має лише один внутрішній стан, він називається автоматом без пам'яті. Стан такого автомата в процесі функціонування не змінюється, оскільки він тільки один. Тому вихідний сигнал автомата без пам'яті залежить лише від вхідного в даному такті сигналу й не залежить від попередніх станів. Закон функціонування таких тривіальних цифрових автоматів без пам'яті описується одним рівнянням 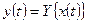
Оскільки логічний стан виходів цифрового автомата без пам'яті залежить тільки від комбінації логічних сигналів на входах в даний момент часу, його називають комбінаційним пристроєм (чи схемою); КП - це асинхронний цифровий автомат.
У загальному вигляді КП (див. рис1.2 ) має N входів, на які подаються сигнали X0, X1, … XN-1, і M виходів, з яких знімаються сигнали Y0, Y1, … YM-1. Отже, КП описується системою логічних функцій
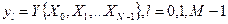
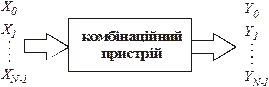
a) б)
Рис. 1.2- Структурні схеми цифрових автоматів
Реалізацію (синтез) КП здійснюють переважно на ЛЕ. Найпростіший випадок реалізації КП - коли схема має один вихід (L=1) .
На відміну від КП значення вихідних сигналів у цифрових автоматах з пам'яттю залежать не тільки від значень вхідних сигналів в даний момент часу, але й від їх попередніх значень. Звідси очевидно, що такі пристрої реалізують функціональний зв'язок вже не між окремими значеннями вхідного та вихідного сигналів, а між їх послідовностями. Тому автомати з пам'яттю називають послідовнісними. На відміну від КП роботу послідовнісних пристроїв (схем) слід розглядати у часі. Отже послідовнісний пристрій (ПП) (рис.1.2,б) повинен мати пам'ять, щоб значення вихідного сигналу залежало від попереднього вхідного сигналу. Ця попередня інформація використовується для побудови ПП у вигляді сукупності так званих внутрішніх сигналів 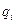 , що виробляють елементи пам'яті (ЕП).– запам'ятовувачі.
, що виробляють елементи пам'яті (ЕП).– запам'ятовувачі.
Основною задачею теорії цифрових автоматів є задача аналізу і синтезу вже розглянутих двох класів цифрових пристроїв. Для цього використовується основний математичний апарат – алгебра логіки. У зв'язку з тим що в основі побудови ПП є КП (див. рис. 1.2,б), задачу синтезу цифрових пристроїв переважно зводять до задачі синтезу КП. Це так званий канонічний метод структурного синтезу ПП.
У табл. 1.7 подані типи КП і ПП, що стоять на різних ступенях інтеграції.
Таблиця 1.7 Класифікація інтегральних схем
| Ступінь інтеграції | Комбінаційні пристрої (схеми) | Послідовнісні пристрої (схеми) |
| МІС | Логічні елементи з різними логічними та функціональними можливостями | Тригери |
| СІС | Перетворювачі кодів, шифратори (дешифратори, мультиплексори), де-мультиплексори, суматори, цифрові компаратори, драйвери | Регістри, лічильники, генератори числових послідовностей |
| ВІС | Арифметико-логічні пристрої, програмовані логічні матриці, постійні запам'ятовувальні пристрої | Багаторозрядні регістри, запам'ятовувальні пристрої великих об'ємів пам'яті тощо |
1.11 Загальні питання синтезу цифрових автоматів
Синтез цифрового пристрою взагалі полягає у побудові такого автомата, який реалізує наперед задану довільним чином функцію "вхід-вихід". Якщо синтез нескінченних автоматів викликає переважно академічний інтерес (важливо лише реалізувати потрібне відображення "вхід-вихід"), синтез скінченних автоматів виходить з практичних задач, і тому завдає, як правило, багато труднощів через додаткові вимоги.
Труднощі залежать здебільшого від способу задавання умов функціонування автомату.
У багатьох випадках з'ясовується, що єдиного методу синтезу скінченних автоматів не існує. Синтез скінченного автомати довільної складності можна поділити на кілька етапів:
· по-блоковий синтез – передбачає поділ всього автомата на окремі блоки, для кожного з яких визначене завдання, яке вони повинні розв'язати, а також накреслені функціональні зв'язки (обмін) між ними;
· абстрактний синтез – полягає у побудові абстрактного автомата (наприклад, його таблиці чи функції переходів і виходів) за обраним способом задавання функції "вхід-вихід"; для ПП тут визначається об'єм. необхідної пам'яті для кожного блока;
· структурний синтез – передбачає побудову структурної схеми автомата; тут встановлюється структура всього автомата з урахуванням структури його вхідних і вихідних сигналів, а також здійснюється вибір елементів для побудови схеми, якщо вони наперед не задані;
· надійнісний синтез – забезпечує надійність (безвідмовність, довговічність, ремонтопридатність) функціонування автомата за допомогою певного перетворення побудованої схеми;
· технічний синтез – кінцевий етап, на якому виявляються спотворення сигналів, що можуть виникати через неідеальність застосовуваних елементів, і вживаються відповідні заходи щодо усунення цих спотворень.
Поділ на етапи дозволяє побачити лише загальну картину процесу синтезу автоматів і, безперечно, у ряді випадках можливі відхилення від розглянутої послідовності. Зокрема, при синтезі простих автоматів етап по-блокового синтезу звичайно опускають і, навпаки, при синтезі особливо складних автоматів до цього етапу доводиться багаторазово повертатись. У деяких випадках доцільно сусідні етапи об'єднати, не розмежовуючи їх, для більшої ефективності процесу синтезу. В інших ситуаціях, враховуючи міркування щодо надійності, етап надійнісного синтезу виконують вже з самого початку.
Перші три етапи синтезу (по-блоковий, абстрактний і структурний) під час проектування цифрових ВІС об'єднують в один комплексний етап так званого функціонально-логічного проектування. При такому процесі проектування велику роль відіграє програмне забезпечення (банк даних) у структурі наскрізної САПР як основного засобу інтеграції різних етапів синтезу ВІС. Після функціонально-логічного проектування при синтезі цифрових ВІС настає етап топологічного проектування, який є складовою частиною технічного синтезу.
При синтезі цифрових автоматів (пристроїв) можуть застосовуватись як евристичні, так і формальні методи. При синтезі КП найбільш поширеними є евристичні методи, які основуються на винахідницькій діяльності розробника. Це творчі методи, які залежать від професійного рівня спеціаліста. Однак вони не забезпечують позитивної ролі формальних методів синтезу, які втілені в САПР і дозволяють стандартизувати процес синтезу. Разом з тим, не слід перебільшувати їх можливості, тому що, як свідчить практика, якість отриманих формальних розв'язків часто поступається перед якістю аналогічних евристичних розв'язків.
Синтез цифрових автоматів (пристроїв) залежно від функціонального базису можна виконувати на різних рівнях (див. табл. 1.7). Зокрема, на найнижчому рівні (МІС) - на ЛЕ або на тригерах, на рівні СІС - на різних функціональних вузлах, на рівні ВІС - на функціональних блоках і пристроях. Ці рівні синтезу цифрових пристроїв в дзеркальним відображенням сучасного рівня технології виготовлення мікросхем. Найбільш складним і трудомістким в процес виготовлення цифрових ВІС - він, фактично, узагальнює всі попередні рівні проектування. Тому проектування цифрових ВІС можна розбити на окремі етапи: логічний, функціональний і архітектурний. На кожному з них розв'язуються певні задачі, які розширюють та поглиблюють знання про ВІС, що підлягає проектуванню .
Основним критерієм ефективності синтезу цифрового автомата е забезпечення мінімуму вартості реалізації логічної функції. При цьому слід мати на увазі, що вартість цифрового пристрою залежить як від часу, так і від рівня технології, на якій він виготовлений.
Поняття вартості цифрового пристрою, синтезованого, наприклад, на рівні МІС, є відмінним від поняття вартості аналогічного пристрою на рівні ВІС чи НВІС.
До питання вартості цифрового пристрою можна підійти з позиції надійності або кількості (числа) елементів, з яких складається даний пристрій, та зв'язків між ними. Безперечно, існує певний взаємозв'язок між обома критеріями, однак в контексті технологічного прогресу спостерігається деяка відмінність. Поняття вартості цифрового пристрою, що побудований на дискретних елементах та ЛЕ, пов'язане з питанням надійності роботи пристрою, однак головну роль відіграє кількість елементів і зв'язків між ними. Власне кількісний фактор тут виступає визначальним при оцінюванні вартості пристрою.
Вартість виготовлення ВІС, зокрема, визначається в основному площею схеми на кристалі і безпосередньо не пов'язана з числом дискретних елементів. Мінімальне число елементів ВІС ще не передбачає мінімальної площі кристалу, а отже, вартості ВІС. Дуже часто схема ВІС з великим числом елементів при високій регулярності структури займає невелику площу і тому є дешевою, бо, крім того, її ще вигідно проектувати. При цьому надійність з’єднань у самому кристалі ВІС є дуже високою порівняно з надійністю з’єднань (тобто точок зовнішніх з’єднань) між самими мікросхемами. Тому поняття вартості ВІС пов'язане в основному з площею кристалу і числом точок зовнішніх виводів (з’єднань). Оскільки розрахунок мінімальної площі схеми ВІС викликає значні труднощі; на практиці традиційно прийнято за основний критерій синтезу цифрового пристрою на ВІС вважати мінімум кількості ЛЕ та їх виводів чи зв'язків між ними. Якщо цифровий пристрій реалізується на ВІС, при використанні схем з високою регулярністю структури типу ІІЗП або ПЛМ зменшення числа виразів у логічній функції, як правило означає зменшення площі схеми, а отже, зниження вартості всього пристрою.
Контрольні запитання
1. В чому відмінність двох класів цифрових пристроїв?
2. Що таке асинхронний та синхронний автомати?
3. Що відображає функція переходу скінченного автомата?
4. Чим визначається абстрактний автомат?
5. Чим відрізняється автомат 1-го роду від автомата 2-го роду?
6. Які цифрові автомати належать до автомата Мілі і автомата Мура?
7. Який автомат називається, комбінаційним?
8. Який автомат називається послідовнісним?
9. В чому полягає синтез КП і ПП?
10. З яких етапів складається синтез скінченного автомата?
11. Особливість синтезу цифрових ВІС.
12. Від чого залежать рівні синтезу скінченних автоматів?