Тема урока: Повторение. Аксиомы планиметрии
План-конспект урока
Предмет: Геометрия
Дата:
№ урока:
Класс: 7
Учитель:Швец Ирина Владимировна
Тема урока: Повторение. Аксиомы планиметрии
Тип урока: Повторение изученного материала
Цели урока: обобщить и систематизировать знания по теме
Задачи урока:
Предметные: осуществлять проверку ЗУН нетрадиционными методами; уметь применять полученные знания в процессе решения задач.
Метапредметные: уметь устанавливать причинно – следственные связи, строить логическое рассуждение, умозаключение. Умение действовать в соответствии с предложенным алгоритмом.
Личностные: готовность к жизненному и личностному самоопределению, знания моральных норм, умения выделять нравственный аспект поведения и соотносить поступки и события с принятыми этическими нормами, ориентация в жизненных ролях и межличностных отношениях (формируются во время выполнения заданий, в которых школьникам предлагается дать собственную оценку)
Регулятивные: уметь поставить учебную цель, задачу на основе того, что уже известно и усвоено; уметь планировать последовательность своих действий для достижения конечного результата.
Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками; постановка вопросов.
Оборудование: доска, конспект, учебник, чертёжные принадлежности, на дверях кабинета лозунг: «Да не войдёт сюда, незнающий геометрии», карточки с символикой: D; ║; Ï; Î; Ç; Ð; ^; ║; ; ; Ç, плакат (об аксиомах).
Ход урока:
1. Организационный момент
2. Вступительное слово учителя
Ребята! Мы закончили изучать первую тему курса планиметрии – «Аксиомы планиметрии». Сегодня на уроке вы покажите их знание, умение применять в различных ситуациях, при решении задач, распознавать предложенную аксиому среди других аксиом. Вы должны показать, как вы умеете правильно излагать свои мысли, рассуждать, доказывать, обосновывать ответ.
3. Индивидуальное задание
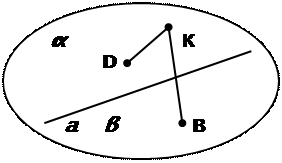
На доске рисунки к четырём аксиомам. Вызывается 4 ученика, которым предлагается по данным распознать аксиому и закончить её «описание».
1) 1 ученик ● А С
● В
К ● D
 |
2) 2 ученик
3) 3 ученик С а) АС > 0, б) если В Î АС, то…
В
А
4) 4 ученик а)
А О В
б) луч проходит между сторонами Ð (ав), Ð (ав) = Ð (ас) + Ð (вс).
4. Фронтальная работа с классом
1) Угадайте, о чём идёт речь.
· а) Это наука о свойствах геометрических фигур, слово греческое, в переводе на русский язык означает «землемерие».
· б) Раздел геометрии, в котором изучаются фигуры на плоскости.
· в) Знаменитый учёный, который свёл воедино все открытия греческих математиков в 13 книгах под общим названием «Начала». В течение двух тысячелетий это научное сочинение было энциклопедией и учебником по математике.
· г) Это слово произошло от глагола «ткнуть».
· Точка – это определяемое понятие или нет? Поэтому эту фигуру относят к каким? А ещё какие простейшие геометрические фигуры вы знаете?
· д) Основные свойства этих и других геометрических фигур выражаются в утверждениях, которые не требуют доказательства. Все эти утверждения можно назвать одним словом. Каким
(Далее обращается внимание на плакат «Откуда эти слова».)
2) Угадайте аксиому (по названию аксиомы необходимо дать её формулировку и наоборот).
· а) Аксиома измерения углов.
· б) Каков бы ни был треугольник, существует равный ему треугольник в заданном расположении относительно заданной полупрямой.
· в) Прямая разбивает плоскость на две полуплоскости.
· г) Аксиома расположения точек на прямой.
· д) Каждый отрезок имеет определённую длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
· е) Аксиома откладывания отрезков.
· ж) От любой полупрямой в заданную полуплоскость можно отложить угол заданной градусной мерой, меньшей 180о, и только один.
· з) Аксиома принадлежности точек и прямых.
3) «Представьте» некоторые аксиомы.
Слушаем тех, кто работал у доски.
5. Работа с символикой
Учитель показывает карточки, с написанными на них символами. Ученики должны сказать, что обозначает каждый из них. (Принимается хоровой ответ)
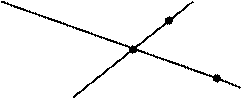6. Опишите ситуацию с помощью математических символов.
в А
● D О
М
с
Ученики работают в тетрадях, а один ученик – у доски. Он же затем её «озвучивает», остальные, если это необходимо, дополняют его ответ.
7. Решение задачи в тетради
Три точки А, В и С лежат на прямой а. Известно, что АВ = 7,4 см, ВС = 3,1 см, АС = 4,4 см. Может ли точка В лежать между точками А и С?
8. Конкурс
Из букв слова ГЕОМЕТРИЯ составьте как можно больше других слов.
(Например,метр, тир, гиря, рот, рог, …)
9. Тест «Верно-неверно»
(Если утвержение верно, то ставят знак «+», а если неверно, то «-». В случае «неверно» дать правильный ответ)
1. В планиметрии рассматриваются свойства фигур в пространстве.
2. Через любые две точки можно провести прямую и притом только одну.
3. Угол – это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.
4. Луч, исходящий из вершины угла и делящий его на два равных угла, называется стороной угла.
5. Для измерения углов используется циркуль.
6. а) Точка А – вершина угла.
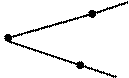В б) Лучи АВ и СА – стороны угла.
А
С
7. Развёрнутый угол равен 360о.
8. Единица измерения углов – сантиметры.
9. АВ = АС – ВС.
А В С
10. На рисунке заштрихована внутренняя область угла.
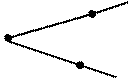А
В
С
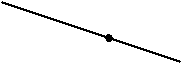11. а а) А Î а.
· А В б) В Ï а.
12. А Ð АСD.
С
D
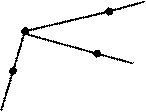13. А ÐАОВ = 33о.
О 44о
77о
В Е
14. Если DАВС = DКРЕ, то АВ = КР, ВС = РЕ, АС = КЕ, ÐА = ÐК, ÐВ = ÐЕ, ÐС = ÐР.
10. Взаимопроверка
Ответы на оборотной стороне доски.
11. Итог урока
· Сколько общих точек имеют две непересекающиеся прямые?
· Точка С лежит на отрезке РМ. Какая из точек С, Р и М лежит между двумя другими?
· Сколько общих точек имеют две пересекающиеся прямые?
· Вывод об уроке, оценки за урок.
В классной работе выполнить письменно:
3. Индивидуальное задание – все 4 задания;
4. Фронтальная работа с классом;
6. Описать ситуацию;
7. Решение задачи;
8. Конкурс;
9. Тест «Верно-неверно»
Домашнее задание: повторить все аксиомы!!!