№6. Уравнения, не разрешённые относительно производной. Уравнения Клеро и Лагранжа. Особые решения.
1. Уравнения 1-ого порядка n-ой степени относительно производной y'
Пусть имеем дифференциальное уравнение
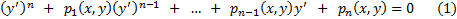
Решаем это уравнение относительно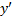 
. Пусть
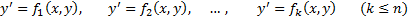
— вещественные решения уравнения (1).
Общий интеграл уравнения (1) выразится совокупностью интегралов:
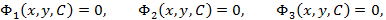
где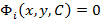 
есть интеграл уравнения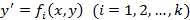 
Таким образом, через каждую точку области, в которой 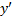принимает вещественные значения, проходит 
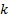интегральных линий.
2. Уравнения вида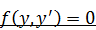 
и 
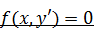
Если уравнения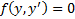 
и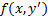 
легко разрешимы относительно 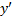, то, разрешая их, получим уравнения с разделяющимися переменными. Рассмотрим случаи, когда эти уравнения не разрешимы относительно .
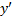А. Уравнение вида 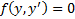разрешимо относительно 
:
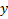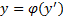
Полагаем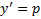 
, тогда 
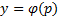. Дифференцируя это уравнение и заменяя 
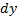на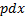 
, получим
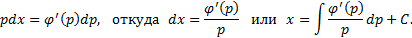
Получаем общее решение уравнения в параметрической форме
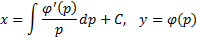
Б . Если уравнение вида 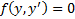неразрешимо (или трудно разрешимо) как относительно 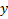, так и относительно 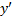, но допускает выражение 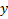и 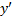через некоторый параметр 
:
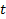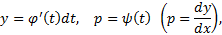
то поступаем следующим образом. Имеем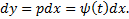 
С другой стороны, 
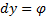, так что 
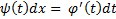и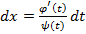 
; отсюда
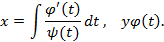
В . Уравнение вида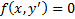 
. Пусть это уравнение разрешимо относительно 
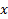, то есть 
.
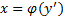Полагая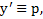 
получим 
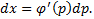Но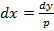 
и, следовательно, 
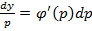, так что
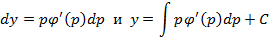
Таким образом,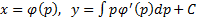 
- общее решение уравнения в параметрической форме (p – параметр).
Уравнение Лагранжа
Имеет вид
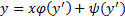
Полагая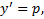 
дифференцируя по 
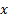и заменяя 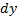на 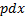, приводим это уравнение к линейному относительно 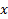как функции 
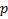. Находя решение этого последнего уравнения 
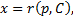получаем общее решение исходного уравнения в параметрической форме:
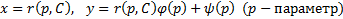
Кроме того, уравнение Лагранжа может иметь ещё особые решения (см. далее) вида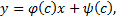 
где 
– корень уравнения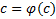 
.
Уравнение Клеро
Имеет вид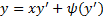 
Метод решения тот же, что и для уравнения Лагранжа. Общее решение уравнения Клеро имеет вид
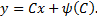
Уравнение Клеро может иметь ещё особое решение, которое получается исключением 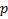из уравнений 
.
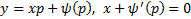Особые решения.
Решение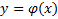 
дифференциального уравнения
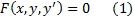
называется особым, если в каждой его точке нарушается свойство единственности, т.е. если через каждую его точку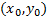 
кроме этого решения проходит и другое решение, имеющее в точке 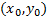ту же касательную, что и решение 
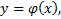но не совпадающее с ним в сколь угодно малой окрестности 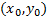. График особого решения будем называть особой интегральной кривой уравнения (1). Если функция 
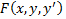и её частные производные 
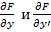непрерывны по всем аргументам 
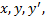то любое особое решение уравнения (1) удовлетворяет также уравнению
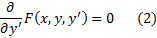
Значит, чтобы отыскать особые решения (1), надо исключить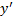 
из уравнений (1) и (2). Полученное после исключения 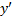из (1) и (2) уравнение
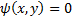
Называется p-дискриминантом уравнения (1), а кривая, определяемая уравнением (3), называется p-дискриминантной кривой (PDK).
Ссылки:
Не разрешённые относительно… , Краснов, стр. 45:
http://mathhelpplanet.com/static.php?p=differentsialnye-uravneniya-pervogo-poryadka--ne-razreshennye-otnositelno-proizvodnoi
Особые решения. Краснов, стр. 59:
http://mathhelpplanet.com/static.php?p=osobye-resheniya-differentsialnyh-uravnenii