Преобразование раунда

Дата: 2025-04-30; Просмотры: 2
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Преобразование раунда состоит из четырех различных преобразований. В нотации на псевдо С это можно записать следующим образом:

Round (State, RoundKey){ ByteSub (State); ShiftRow (State); MixColumn (State); AddRoundKey (State, RoundKey); }

Заключительный раунд алгоритма немного отличается и выглядит следующим образом:

FinalRound (State, RoundKey){ ByteSub (State); ShiftRow (State); AddRoundKey (State, RoundKey);}

Как мы видим, заключительный раунд эквивалентен остальным, за исключением того, что отсутствует слой MixColumn.

 

Преобразование ByteSub

Преобразование ByteSub является нелинейной байтовой подстановкой, выполняющейся для каждого байта состояния независимо. Таблица подстановки является обратимой и сконструирована в виде композиции двух преобразований:

1. Во-первых, берется мультипликативная инверсия в GF (28) с определенным выше представлением. '00' отображается сам в себя.

2. Затем применяется афинное (в GF (2)) преобразование над каждым байтом, определяемое следующим образом (рис. 7):

 

Рис. 7.

 

Применение описанного S-box ко всем байтам состояния обозначается как ByteSub (State) – заменяется каждый байт и над каждым байтом выполняется преобразование (рис. 7, 8).

 

 

· ByteSub – табличная подстановка 8х8 бит (рис. 8) аi,j – байт до преобразования, bi,j – байт после преобразования.

 


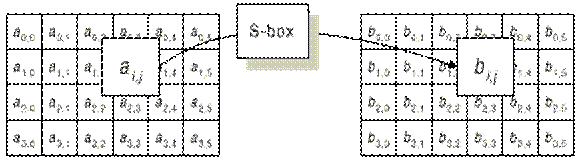
Рис. 8.

Преобразование ShiftRow

· ShiftRow – сдвиг строк в двумерном массиве на различные смещения (рис. 9),

 


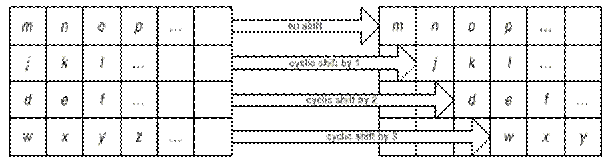
Рис. 9.

 

В ShiftRow строки состояния циклически сдвигаются на различные значения. Нулевая строка не сдвигается. Строка 1 сдвигается на С1 байтов, строка 2 на С2 байтов, строка 3 на С3 байтов. Величины С1, С2 и С3 зависят от Nb. Значения приведены в следующей таблице.

Таблица 3

Величина сдвига в зависимости от длины блока

Nb С1 С2 С3
4 1 2 3
6 1 2 3
8 1 3 4

 

Операция сдвига строк на указанные значения обозначается как

ShiftRow (State)

Инверсией для ShiftRow является циклический сдвиг трех нижних строк соответственно на Nb - С1, Nb - С2 и Nb - С3 байт, чтобы байт в позиции j в строке i перемещался в позицию (j + Nb - Ci) mod Nb.