Трапеція – це чотирикутник, в якому дві сторони паралельні. Ці паралельні сторони називаються основами трапеції, дві інші сторони – бічними сторонами.
Очевидно, паралелограм є частинний випадок трапеції. Якщо бічні сторони трапеції рівні між собою, то трапеція називається рівнобічною (рис.1.21, АВ = С D).
Рівнобічна трапеція має такі властивості:
1) Кути, прилеглі до основи рівнобічної трапеції, рівні. (Справджується і обернене твердження: якщо кути, прилеглі до основи трапеції, рівні, то така трапеція рівнобічна).
2) Діагоналі рівнобічної трапеції рівні.
3) Сума протилежних кутів рівнобічної трапеції дорівнює 180°.
Відрізок, що сполучає середини бічних сторін трапеції, називається її середньою лінією (рис.1.21, MN – середня лінія,  ).
).
Середня лінія трапеції паралельна її основам і дорівнює їх півсумі (рис.1.21, MN  AD , MN
AD , MN  ВС, MN =).
ВС, MN =).

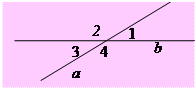
1.20°. При перетині двох прямих a і b утворилось 4 кути. Задайте кожній з умов (А – Д) можливі наслідки (1 – 5).
| А) Ð1 = Ð3; | 1) Ð3 = Ð4 = 90º; |
| ||||||||||
| Б) Ð2 + Ð3 = 180º; | 2) Ð1 = Ð2 = Ð4 = 90º; | |||||||||||
| В) Ð1 = Ð2 = 90º; | 3) Ð1 і Ð4 – суміжні; | |||||||||||
| Г) Ð2 + Ð4 = 260º; | 4) Ð1 і Ð3 – гострі; | |||||||||||
| Д) Ð3 = 90º. | 5) Ð2 і Ð4 – вертикальні. |
1.21°. Умовами (1 – 7) вказано градусну міру деяких кутів. Виберіть серед них ті, які можуть бути суміжними.
| 1) 18º; | 2) 72º; | 3) 128º; | 4) 62º; | 5) 28º; | 6) 108º; | 7) 38º. | |||||
| А) 1 і 2; | Б) 2 і 6; | В) 3 і 4; | Г) 1 і 7; | Д) 2 і 5. | |||||||
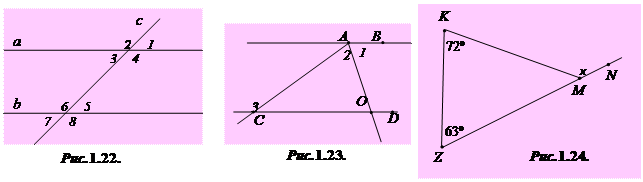 |
1.22°. Виберіть правильний висновок, користуючись даними рисунка 1.22 , якщо відомо, що Ð1 = Ð7.
| А) a || b; | Б) a 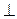 b; b;
| В) a 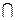 b. b.
|
1.23°°. Знайдіть градусну міру Ð3 (рис. 1.23), якщо CD || AB, Ð1 = Ð2 і Ð2 = 72º.
| А) 72º; | Б) 144º; | В) 108º; | Г) 36º; | Д) 124º. |
1.24°. Знайдіть градусну міру зовнішнього кута KMN трикутника KMZ (рис. 1.24).
| А) 135º; | Б) 125º; | В) 108º; | Г) 117º; | Д) 45º. |





 1.25°. Знайдіть градусну міру кута між бісектрисою кута при вершині
1.25°. Знайдіть градусну міру кута між бісектрисою кута при вершині
рівнобедреного трикутника та його бічною стороною, якщо кути трикутника
ABC відносяться як 3 : 4 : 3.
| А) 18º; | Б) 36º; | В) 72º; | Г) 60º; | Д) 30º. |
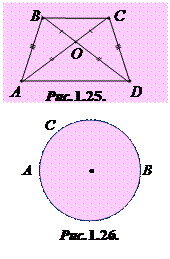 1.26°. Визначте, користуючись даними рисунка1.25 правильні рівності.
1.26°. Визначте, користуючись даними рисунка1.25 правильні рівності.
| А) ∆ABO = ∆OCD; | Г) ÐAOB = ÐDOC; |
| Б) ∆AOB = ∆COD; | Д) ÐBAO = ÐDCO; |
| В) BA = CD; | Е) ÐBAO = ÐCDO. |
1.27°. Знайдіть, користуючись рисунком 1.26, кути трикутника BOC.
| А) 48º, 48º, 84º; | В) 24º, 132º, 24º; | |
| Б) 132º, 48º, 48º; | Г) 42º, 90º, 48º; | Д) 48º, 132º, 20º. |
1.28°. Ідентифікуйте кожному шестикутнику периметра Р, коло, радіуса R, описаного навколо нього.
А) 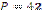 см; см;
| 1) 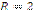 см; см;
|
Б) 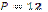 см; см;
| 2) 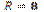 см; см;
|
В) 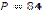 см; см;
| 3) 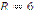 см; см;
|
Г) 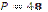 см; см;
| 4) 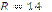 см; см;
|
Д) 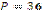 см. см.
| 5) 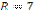 см. см.
|
| А | |
Б 
| |
| В | |
| Г | |
| Д |
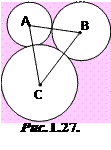
1.29°. Обчисліть периметр трикутника з вершинами у центрах трьох кіл з радіусами 6 см, 7 см і 8 см, що попарно дотикаються зовні (рис.1.27).
| А) 28 см; | В) 27 см; | |
| Б) 29 см; | Г) 42 см; | Д) 21 см. |
1.30°. Виберіть вирази, якими визначаються радіус вписаного кола у правильний трикутник зі стороною а та радіус описаного навколо нього кола:
1) 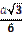 ; ;
| 2) 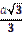 ; ;
| 3) 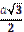 ; ;
| 4)  ; ;
| 5) 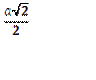 . .
|
| А) 1 і 2; | Б) 2 і 3; | В) 3 і 4; | Г) 4 і 5; | Д) 1 і 5. |
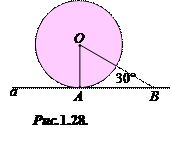
1.31°. Знайдіть діаметр кола, якщо пряма a є дотичною до нього,
A – точка дотику, OB = 12 см та утворює з дотичною кут 30º (рис.1.28).
| А) 24 см; | Б) 12 см; | В) 6 см; | Г) 18 см; | Д) 4 см. |
1.32°. Сторона квадрата 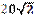 см. Укажіть довжину радіуса кола,
см. Укажіть довжину радіуса кола,
вписаного у цей квадрат.
| А) 20 см | Б) 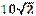 см см
| В) 10 см | Г)  см см
| Д) 5 см. |
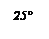 1.33°. Одна з основ трапеції на 8 см більша за іншу, а середня лінія трапеції дорівнює 10 см. Знайдіть меншу основу трапеції.
1.33°. Одна з основ трапеції на 8 см більша за іншу, а середня лінія трапеції дорівнює 10 см. Знайдіть меншу основу трапеції.
| А) 2 см; | Б) 4 см; | В) 6 см; | Г) 8 см; | Д) 10 см. |
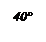 1.34°. Обчисліть площу ромба, діагоналі якого дорівнюють 10 см і 36 см.
1.34°. Обчисліть площу ромба, діагоналі якого дорівнюють 10 см і 36 см.
| А) 90 см2; | Б) 92 см2; | В) 180 см2; | Г) 184 см2; | Д) 360 см2. |
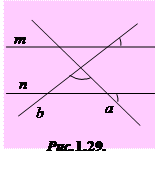
1.35°°. Знайдіть, користуючись даними рисунка 1.29, кут між прямими a і b,
якщо прямі m і n паралельні.
| А) 50º; | Б) 80º; | В) 100º; | Г) 65º; | Д) 115º. |
1.36°°. Визначте довжини радіусів двох кіл, що дотикаються зовні, якщо відстань між їх центрами 18 см, а довжина одного з них становить 50 % довжини іншого.
| А) 9 см і 6 см; | В) 12 см і 6 см; | |
| Б) 10 см і 8 см; | Г) 14 см і 4 см; | Д) 24 см і 12 см. |
1.37°°. Укажіть вираз, що визначає довжину кола, яке обмежує круг площею см2.
| А) см; | Б) см; | В) 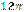 см; см;
| Г) 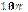 см; см;
| Д) см. |
1.38°°. Знайдіть площу круга, вписаного в квадрат зі стороною 6 см.
| А) см2; | Б) 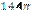 см2; см2;
| В) 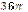 см2; см2;
| Г) 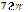 см2; см2;
| Д) 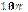 см2. см2.
|
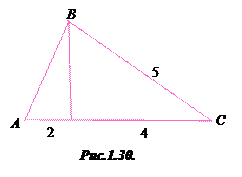
1.39°°. Знайдіть площу трикутника, користуючись даними рисунка 1.30, де довжини відрізків наведені в см.
| А) 6 см2; | Б) 9 см2; | В)12 см2; | Г) 24 см2; | Д) 30 см2. |
1.40°°. Визначте периметр рівнобедреного трикутника, якщо точка дотику, вписаного у нього кола, ділить його бічну сторону на відрізки 6 см і 5 см. Виберіть правильну комбінацію можливих відповідей.
| 1) 21 см; | 2) 32 см; | 3) 23 см; | 4) 34 см; | 5) 33 см. |
| А) 1 або 2; | Б) 2 або 4; | В) 2 або 3; | Г) 3 або 5; |  Д) 4 або 5. Д) 4 або 5.
|
1.41°°. Знайдіть сторону ВС трикутника ABC, який вписано в коло
радіуса R
(рис.1.31).
| А) R; | Б) 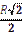 ; ;
| В) 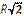 ; ;
| Г) 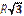 ; ;
| Д) 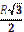 . .
|
1.42°°. Ідентифікуйте парами сторону правильного трикутника а та відповідний
радіус r вписано в нього кола.
А) 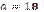 см; см;
| 1) 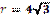 см; см;
| А | |
Б) 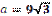 см; см;
| 2) 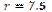 см; см;
| Б 
| |
В) 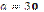 см; см;
| 3) 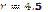 см; см;
| В | |
Г) 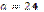 см; см;
| 4) 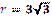 см; см;
| Г | |
Д) 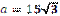 см. см.
| 5) 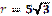 см. см.
| Д |
1.43°°. Радіус кола, вписаного в квадрат, дорівнює 5 см. Знайдіть діагональ квадрата.
| А) см; | Б)  см; см;
| В)  см; см;
| Г)  см; см;
| Д)  см. см.
|
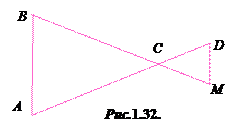 1.44°°. На рисунку 1.32 зображено два трикутники АВС і СDМ, сторони яких АВ і MD – паралельні. Знайдіть довжину відрізка AD, якщо
1.44°°. На рисунку 1.32 зображено два трикутники АВС і СDМ, сторони яких АВ і MD – паралельні. Знайдіть довжину відрізка AD, якщо 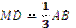 ,
,  см.
см.
| А) 3 см; | Б) 4,5 см; | В) 6 см; | Г) 7,5 см; | Д) 9 см. |
1.45°°. Укажіть кількість сторін правильного многокутника, внутрішній кут якого дорівнює 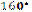 .
.
| А) 12; | Б) 14; | В) 16; | Г) 18; | Д) 20. |
1.46°°. Знайдіть периметр ромба, діагоналі якого дорівнюють 24 см і 18 см.
| А) 120 см; | Б) 60 см; | В) 84 см; | Г) 108 см; | Д) 144 см. |
1.47°°. Відомо, що периметр паралелограма дорівнює 48 см, а одна з його сторін на 8 см довша за іншу. Знайдіть меншу сторону паралелограма.
| А) 8 см; | Б) 16 см; | В) 6 см; | Г) 12 см; | Д) 10 см. |
1.48°°. Зовні рівнобедреного трикутника ABC побудували два рівні кути ABM і CBK, сторони яких перетнули продовження основи AC відповідно у точках M і K. Доведіть рівність трикутників MBC і KBA (рис. 1.33а).
1.49°°. З точки кола проведено дві взаємно перпендикулярні хорди довжиною 5 см і 12 см. Знайдіть відстань між кінцями хорд.
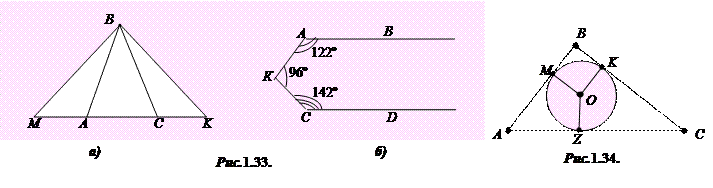
1.50·. Визначте взаємне розміщення двох прямих AB і CD за даними рисунка 1,33б. Відповідь обґрунтуйте.
1.51·. У трикутник ABC вписано коло (рис. 1.34), точки дотику якого M , Z поділяють дві його сторони AB i AC на відрізки, різниця яких відповідно дорівнює 3 см і 4 см (AM > MB , AZ > ZC). Знайдіть сторони трикутника ABC, якщо його периметр дорівнює 28 см.
1.52·. Навколо рівностороннього трикутника описане коло, радіус якого дорівнює  см. Обчисліть радіус вписаного кола.
см. Обчисліть радіус вписаного кола.
1.53·. Навколо кола описана рівнобічна трапеція, кут при основі якої дорівнює  Висота трапеції – 7 см. Знайдіть довжину середньої лінії трапеції.
Висота трапеції – 7 см. Знайдіть довжину середньої лінії трапеції.
1.54·. Навколо кола описана рівнобічна трапеція, кут при основі якої дорівнює  Середня лінія трапеції дорівнює
Середня лінія трапеції дорівнює  см. Знайдіть довжину висоти трапеції.
см. Знайдіть довжину висоти трапеції.
1.55·. Знайдіть бічну сторону рівнобедреного трикутника, основа якого дорівнює 16 см, а висота проведена до неї, – 15 см.
1.56·. Висота АМ трикутника АВС ділить його сторону ВС на відрізки ВМ і МС. Знайдіть довжину відрізка МС, якщо  см,
см, 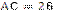 см,
см, 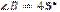 .
.
1.57·. Сторона ромба дорівнює 10 см, а одна з діагоналей – 12 см. Знайдіть радіус вписаного в ромб кола.
1.58·. У колі, радіусом 15 см, на відстані 12 см від його центра проведено хорду. Знайдіть довжину цієї хорди.
1.59·. Бісектриса тупого кута паралелограма ділить його сторону на відрізки 6 см і 10 см, рахуючи від вершини гострого кута. Обчисліть площу паралелограма, якщо його гострий кут дорівнює 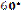 .
.
1.60··. У колі проведено дві хорди, що перетинаються. Одна із них точкою перетину поділилася навпіл, а друга – на частини довжиною 5 см і 20 см. Знайдіть довжину кожної хорди.
1.61··. З точки поза колом проведено січну і дотичну. Знайдіть довжину дотичної, якщо вона на 5 см більша від зовнішньої частини та на стільки ж менша від внутрішньої частини січної.
1.62··. З точки поза колом проведено січну і дотичну, сума довжин яких дорівнює 15 см, а зовнішня частина січної на 2 см менша від дотичної. Знайдіть довжини січної і дотичної.
1.63··. Знайдіть площу прямокутного трикутника, якщо точка дотику вписаного кола ділить гіпотенузу на відрізки 6 см і 9 см.
1.64··. У прямокутній трапеції менша основа дорівнює 8 см, а менша бічна сторона –  см. Знайдіть площу трапеції, якщо один із її кутів дорівнює
см. Знайдіть площу трапеції, якщо один із її кутів дорівнює 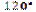 .
.
1.65··. Навколо трапеції, основи якої дорівнюють 40 см і 14 см, а висота – 39 см, описано коло. Знайдіть його радіус.
1.66··. а) Діагоналі трапеції дорівнюють 20 см і 15 см, висота - 12 см. Обчисліть площу трапеції.
б) Діагоналі трапеції дорівнюють 30 см і 26 см, а висота – 24 см. Обчисліть площу трапеції.
1.67··. Більша діагональ ромба дорівнює 24 см, а радіус вписаного кола – 6 см. Обчисліть площу ромба.
1.68··. Сторони трикутника дорівнюють 17 см, 25 см і 28 см. Коло з центром на найбільшій стороні дотикається до двох інших сторін. Обчисліть площу круга.
1.69··. Знайдіть площу паралелограма, якщо його сторони дорівнюють 6 см і 4 см, а кут між діагоналями – 60°.








