Властивості рівнобедреного трикутника: кути при основі трикутника рівні; висота, проведена до основи трикутника, є також бісектрисою і медіаною.
Властивості рівностороннього трикутника: усі кути трикутника - рівні (кожний кут дорівнює 60°); кожна з трьох висот трикутника є також бісектрисою і медіаною; центр кола, описаного навколо трикутника, збігається з центром кола, вписаного в нього.
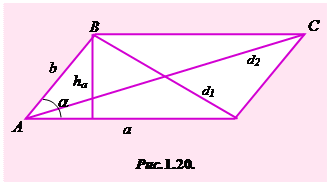
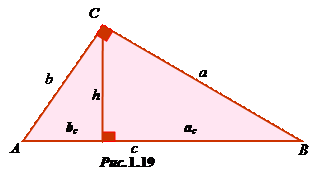 Прямокутний трикутник має сторону, яка лежить проти прямого кута – гіпотенузу (с) та дві сторони, які утворюють прямий кут – катети (а, b) (рис.1.19). Сторони кожного прямокутного трикутника а, b, і c (с – гіпотенуза) зв’язані між собою співвідношенням, що називається теоремою Піфагора: с2 = а2 + b2, яка читається так: квадрат довжини гіпотенузи дорівнює сумі квадратів довжин катетів.
Прямокутний трикутник має сторону, яка лежить проти прямого кута – гіпотенузу (с) та дві сторони, які утворюють прямий кут – катети (а, b) (рис.1.19). Сторони кожного прямокутного трикутника а, b, і c (с – гіпотенуза) зв’язані між собою співвідношенням, що називається теоремою Піфагора: с2 = а2 + b2, яка читається так: квадрат довжини гіпотенузи дорівнює сумі квадратів довжин катетів.
Властивості прямокутного трикутника:
1) Катет є середнім пропорційним між гіпотенузою і проекцією цього катета на гіпотенузу: b2 = bс 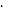 с і а2 = ас
с і а2 = ас 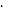 с (рис. 1.19);
с (рис. 1.19);
2) Висота, проведена з вершини прямого кута, є середнім пропорційним між проекціями катетів на гіпотенузу: h2= bс · ас ;
3) Центр кола, описаного навколо прямокутного трикутника, лежить на середині гіпотенузи.
4) Для сторін прямокутного трикутника істинні відношення: sin Ð A = 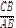 ; cos Ð A =
; cos Ð A = 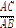 .
.
5) Запам’ятайте!
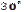
| 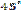
| 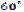
| Вказівка для кращого запам’ятовування: 1) запишіть риски дробів для кожного значення виразу sin 2) запишіть у чисельниках числа: 1, 2, 3 (для sin 3) допишіть знак радикала до кожного чисельника дробу. Враховуючи те, що | |
sin 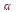
| 
| 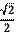
| 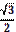
| |
cos 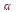
| 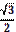
| 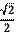
| 
|
 Опуклі чотирикутники.
Опуклі чотирикутники.
Чотирикутник, протилежні сторони якого попарно паралельні, називається паралелограмом.
Властивості паралелограма:
1) Середина діагоналі паралелограма є його центром симетрії.
2) Протилежні сторони паралелограма рівні.
3) Протилежні кути паралелограма рівні.
4) Кожна діагональ паралелограма ділить його на два рівні трикутники.
5) Діагоналі паралелограма діляться точкою перетину пополам.
6) Сума квадратів діагоналей паралелограма (d1 і d2) дорівнює сумі квадратів усіх його сторін:
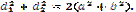
Щоб довести, що деякий заданий чотирикутник є паралелограмом, треба, згідно з означенням, впевнитися у паралельності протилежних його сторін. Інколи такі міркування є громіздкими, а інколи – зайвими. Оскільки існують інші доведені ознаки, на підставі яких можна твердити, що даний чотирикутник є справді паралелограм.
Якщо у чотирикутнику справджується будь-яка з таких умов: 1) протилежні сторони попарно рівні; 2) дві протилежні сторони рівні і паралельні; 3) протилежні кути попарно рівні; 4) діагоналі, у точці перетину, поділяються пополам, то такий чотирикутник є паралелограмом.
Прямокутник – це паралелограм, в якому всі кути рівні. Оскільки сума кутів чотирикутника дорівнює 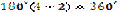 , то у прямокутника всі кути прямі. Прямокутник має всі властивості паралелограма і, окрім того, - ще таку властивість: діагоналі прямокутника рівні між собою.
, то у прямокутника всі кути прямі. Прямокутник має всі властивості паралелограма і, окрім того, - ще таку властивість: діагоналі прямокутника рівні між собою.
Для прямокутника справджується і обернена теорема про те, що коли у паралелограмі діагоналі рівні, то такий паралелограм є прямокутником. Ця теорема є ознакою прямокутника.
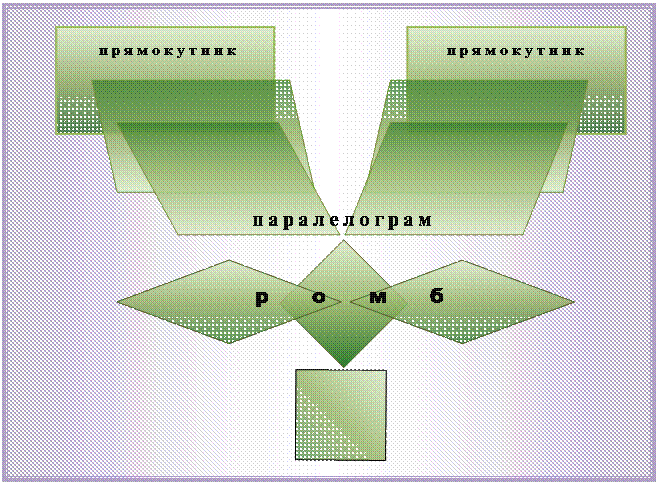 Ромб – це паралелограм, в якому всі сторони рівні. Крім загальних властивостей паралелограма, ромб має ще й інші властивості, характерні лише йому. Діагоналі ромба взаємно перпендикулярні і поділяють його кути пополам. Справджується і обернена теорема, яка є ознакою ромба: якщо у паралелограмі діагоналі взаємно перпендикулярні або якщо у ньому діагоналі поділяють кути пополам, то такий паралелограм є ромб.
Ромб – це паралелограм, в якому всі сторони рівні. Крім загальних властивостей паралелограма, ромб має ще й інші властивості, характерні лише йому. Діагоналі ромба взаємно перпендикулярні і поділяють його кути пополам. Справджується і обернена теорема, яка є ознакою ромба: якщо у паралелограмі діагоналі взаємно перпендикулярні або якщо у ньому діагоналі поділяють кути пополам, то такий паралелограм є ромб.
Квадрат – це паралелограм, в якому всі кути рівні і всі сторони рівні. Отже, квадрат – це прямокутник з рівними сторонами або квадрат – це ромб з рівними кутами (прямими). Очевидно, що квадрат має всі властивості прямокутника і ромба.









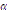 і cos
і cos 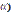 ;
;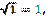 отримуємо заповнену таблицю.
отримуємо заповнену таблицю.