Трикутник та його елементи.

Дата: 2025-06-02; Просмотры: 8

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Трикутником називається фігура, яка складається із трьох точок, що не лежать на одній прямій, і трьох відрізків, що попарно сполучають ці точки. Розглянемо 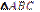(рис. 1.17), в якому виділяють 6 основних елементів: 3 внутрішні кути 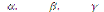і 3 відповідно протилежні їм сторони а, b, c.

Трикутник називається тупокутним, прямокутним або гострокутним, якщо його найбільший внутрішній кут відповідно більший, дорівнює або менший від 90^°.

Трикутник називається рівнобедреним, якщо в нього дві сторони рівні (бічні сторони). Основою рівнобедреного трикутника є та сторона, яка не дорівнює жодній з інших двох рівних сторін.

Трикутник, усі сторони якого рівні, називається рівностороннім (або правильним).

Співвідношення між сторонами і кутами трикутника (рис.1.17):

проти більшої сторони лежить більший кут і навпаки; проти рівних сторін лежать рівні кути; теорема синусів: 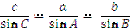; теорема косинусів: 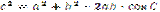(квадрат будь-якої сторони трикутника дорівнює сумі квадратів двох інших сторін без подвоєного добутку цих сторін на косинус кута між ними).

Трикутник повністю визначається будь-якою з таких трійок своїх основних елементів: або двома сторонами і кутом між ними, або однією стороною і двома кутами, або трьома сторонами. Наприклад, △ зі сторонами а, b, c можна задати так:

1) a, b i C; b, c i A; a, c i B;

2) a, B i C; b, A i C; c, A i B;

3) a, b і c.

Співвідношення між внутрішніми і зовнішніми кутами трикутника : будь-який зовнішній кут трикутника дорівнює сумі двох внутрішніх кутів, не суміжних з ним.

З трьох відрізків можна утворити трикутник тоді і тільки тоді, коли будь-яка його сторона менша за суму і більша за різницю двох інших його сторін. У будь-якому трикутнику можна провести три медіани, три бісектриси і три висоти.

Властивості бісектриси кута трикутника:

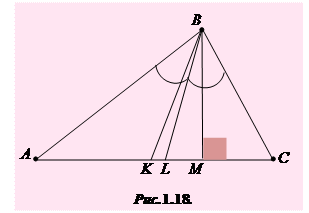
Бісектриси трикутника перетинаються в одній точці, яка лежить всередині трикутника і є центром вписаного в трикутник кола. Бісектриса ділить протилежну сторону на частини, пропорційні прилеглим до неї сторонам (рис. 1.18; BL - бісектриса, AL : L С = AB : BC).

Основні властивості медіан трикутника:

1. Медіани трикутника перетинаються в одній точці, що лежить всередині трикутника.

2. Медіани трикутника точкою їхнього перетину діляться у відношенні 2 : 1 (рахуючи від вершин трикутника).

3. Медіана ділить трикутник на два трикутники, площі яких рівні (рис. 1.18; BK – медіана, ).

4. Три медіани трикутника ділять трикутник на шість трикутників, площі яких рівні.

Прямі на яких лежать висоти трикутника перетинаються в одній точці – ортоцентрі трикутника, яка може міститися у внутрішній або зовнішній області трикутника. Висоти трикутника, опущені на сторони трикутника а, b, і с, позначаються h_a, h_b, h_c відповідно. Висота трикутника h_a визначається через сторони за формулою 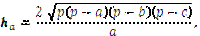де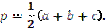

Медіана трикутника m_a, проведена до сторони а, визначається через сторони трикутника формулою .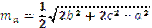

У кожному трикутнику можна побудувати три середні лінії – відрізки, які сполучають середини двох сторін трикутника. Середня лінія трикутника паралельна третій стороні трикутника та дорівнює її половині. Середня лінія трикутника відтинає від трикутника подібний трикутник. Площа відрізаного трикутника відноситься до площі основного трикутника у співвідношенні 1 : 4.