Навколо кожного правильного многокутника можна описати коло або у кожний правильний многокутник можна вписати коло.
У правильному многокутнику центри описаного і вписаного кіл співпадають. Спільний центр описаного і вписаного кіл називається центром правильного многокутника. Радіус вписаного кола називають апофемою правильного многокутника.
Кут, утворений двома радіусами, проведеними у суміжні вершини правильного многокутника, називається його центральним кутом. Усі центральні кути правильного многокутника між собою рівні, вони дорівнюють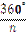 
, де n – кількість сторін (кутів) многокутника.
У правильному n – кутнику, як і в довільному n – кутнику, сума всіх кутів (внутрішніх) становить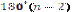 
. Тому кожний його кут визначається за формулою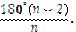 
Коло, вписане у правильний многокутник, дотикається до його сторін в їх серединах. Центр кола, вписаного у правильний многокутник, є точкою перетину серединних перпендикулярів до його сторін (рис. 1.15).
Якщо сторона правильного многокутника дорівнює а, радіус, вписаного у нього кола, – r, а радіус описаного навколо нього кола –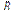 
, то між ними існує взаємозв’язок, що виражається формулами:
, 
.
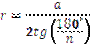Якщо n = 3 (правильний трикутник), то: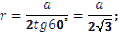 
.
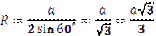Якщо n = 4 (правильний чотирикутник), то: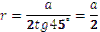 
; 
.
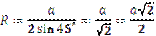Якщо n = 6 (правильний шестикутник), то: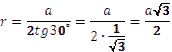 
; 
.
 |
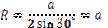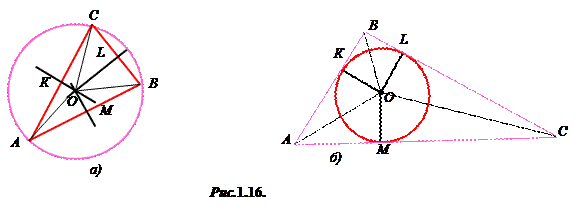Найпростішим многокутником є трикутник. У будь-який трикутник можна вписати коло, при чому тільки одне (рис.1.16,б). На рис.1.16,б зображено коло з центром О, вписане в трикутник АВС,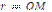 
– його радіус. Центр кола, вписаного в трикутник, є точкою перетину його бісектрис і знаходиться всередині площини цього трикутника. Оскільки площу трикутника знаходять за формулою: 
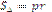, де р – півпериметр трикутника, то звідси 
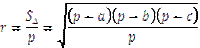, де а, b, с – сторони трикутника. Центр кола, вписаного в трикутник, рівновіддалений від його сторін.
Чи можна у будь-який чотирикутник вписати коло?
Відповідь. Не можна. У чотирикутник можна вписати коло, при умові, що суми довжин його протилежних сторін рівні.
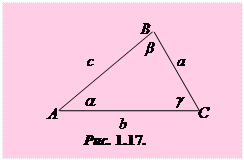
Навколо довільного трикутника можна описати коло, причому тільки одне (рис. 1.16,а). Центр кола, описаного навколо трикутника, є точкою перетину серединних перпендикулярів проведених до його сторін. Центр кола О, описаного навколо трикутника АВС, рівновіддалений від його вершин.
На рис. 1.16, а зображено коло з центром О, описане навколо трикутника АВС,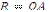 
– його радіус. Якщо радіус описаного кола R, сторони трикутника, вписаного в коло, а, b і с, то 
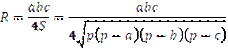, де p – півпериметр трикутника.
Чи можна описати коло навколо довільного чотирикутника?
Відповідь. Не можна. Навколо чотирикутника можна описати коло тоді, коли суми протилежних кутів рівні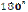 
.