Взаємне розміщення прямих на площині.
Дві прямі на площині можуть перетинатися лише в одній точці або не перетинатися, тобто бути паралельними. При перетині двох прямих утворюються суміжні і вертикальні кути. Суміжні кути доповнюють один одного до 180°, а вертикальні – рівні. Кутова міра меншого з них називається кутом між прямими. На рис. 1.3 зображено дві прямі AD і BC, які перетинаються в точці О, утворюючи суміжні та вертикальні кути:
1) 
, 
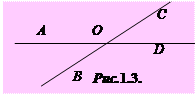
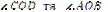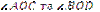– вертикальні;
2) 
, 
,
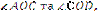
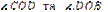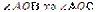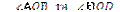– суміжні.
Якщо один з кутів при перетині двох прямих дорівнює 90°, то всі інші – суміжні та вертикальні кути, також дорівнюють 90°. Такі прямі називають взаємно перпендикулярними. Записують AD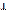 
BC або 
.
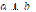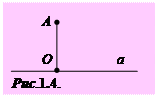Відстанню від точки А до прямої а (рис.1.4) називається довжина
відрізка ОА, перпендикулярного до прямої, де точка О – основа
перпендикуляра. Відстань від точки А до будь-якої точки прямої а,
відмінної від точки О, більша за відстань від точки А до прямої а.
Тобто будь-який відрізок АХ, де Х - точка прямої а, довший за відрізок ОА.
Дві різні прямі а і b, які лежать в одній площині, називаються паралельними, якщо вони не мають жодної спільної точки. Коротко записують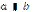 
. Якщо прямі не паралельні 
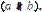то вони перетинаються. 
| Внаслідок перетину двох прямих третьою прямою утворюється вісім кутів (рис.1.5): - Внутрішні односторонні (кути 4 і 5, 3 і 6); - Внутрішні різносторонні (кути 3 і 5, 4 і 6); - Зовнішні односторонні (кути 1 і 8, 2 і 7); - Зовнішні різносторонні (кути 1 і 7, 2 і 8); - Відповідні кути (кути 1 і 5, 2 і 6, 8 і 4, 7 і 3) |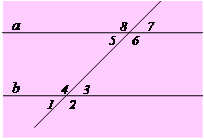  
|
Ознаки паралельності прямих:
1) Якщо при перетині двох прямих а і b третьою прямою внутрішні (або зовнішні) різносторонні кути рівні (або внутрішні односторонні в сумі становлять 180°), то а і b паралельні.
2) 
Дві прямі, паралельні третій, паралельні між собою.
Теорема (про рівні відрізки, теорема Фалеса):
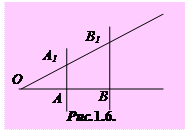
Якщо на одній прямій відкласти кілька рівних відрізків і через їхні кінці провести паралельні прямі, що перетинають другу пряму, то, вони відітнуть на другій прямій теж рівні відрізки. Наприклад, якщо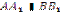 
, причому ОА= A В, то ОА1=А1В1 (рис. 1.6).
Коло і круг.
Форми круга та кола ми зустрічаємо повсюди. Кругом з центром О і радіусом R називається фігура, яка утворена з усіх точок площини, віддалених від точки O на відстань, не більшу R. Круг обмежений колом. Колом з центром О і радіусом R називається множина точок площини, віддалених від точки O на відстань, що дорівнює R (рис. 1.7,а). О – центр кола (круга). Відрізки, що з’єднують центр з точками кола, мають довжину R і називаються радіусами кола (круга).
Частина круга, на які він ділиться двома радіусами, називаються круговими секторами (рис. 1.7,б).
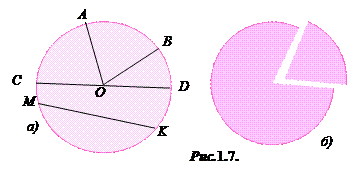Хорда – відрізок, що з’єднує дві точки кола (MK), – ділить круг на два сегменти, а коло – на дві дуги. Діаметр – найбільша хорда кола (CD).
Через три точки, що не лежать на одній прямій, проходить єдине коло. Діаметр, перпендикулярний до хорди, поділяє пополам цю хорду і обидві дуги, які стягуються нею і навпаки, якщо діаметр, проведений через середину хорди, то він перпендикулярний до неї і поділяє пополам дугу, яку стягує ця хорда (рис. 1.8,а).
Дуги, що містяться між паралельними хордами, рівні між собою. Рівні дуги стягуються рівними хордами і, навпаки, рівні хорди стягують рівні дуги. Більша дуга, що не перевищує 180°, стягується більшою хордою і, навпаки, більша хорда стягує більшу дугу (рис. 1.8,а).
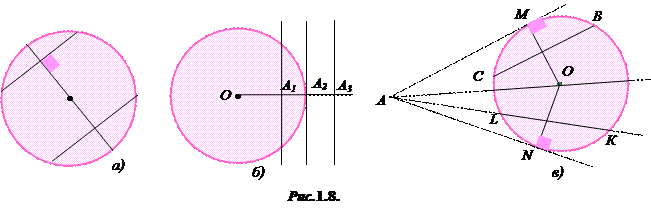
Рівні хорди однаково віддалені від центра і, навпаки, хорди, однаково віддалені від центра, між собою рівні. Більша з двох хорд менше віддалена від центра і, навпаки, та з двох хорд більша, яка менше віддалена від центра (рис. 1.8,а).
Яке розміщення прямої з колом?
Розглянемо коло з центром О і пряму l (рис. 1.8,б). З точки О проведемо перпендикуляр на пряму l. Нехай А є основа цього перпендикуляра. Можливі три випадки, коли точка А міститься поза колом (А3), на колі (А2) і всередині кола (А1). У кожному з цих випадків коло і пряма l: або не мають спільних точок, або мають лише одну спільну точку А2 (l – дотична до кола), або мають лише дві спільні точки (l – січна).
Пряма, що проходить через точку кола, є дотичною до кола тоді і тільки тоді, коли вона перпендикулярна до радіуса, проведеного у цю точку. Якщо дотична паралельна хорді кола, то точка дотику поділяє пополам дугу, яку стягує хорда (рис. 1.8,в; АМ 
СВ,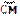 
= 
) .
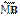Якщо з однієї точки до кола проведені дві дотичні, то відрізки цих дотичних від точок дотику до даної точки рівні між собою, а промінь, проведений через дану точку і центр кола, поділяє пополам кут між дотичними (рис. 1.8,в; АМ= AN ,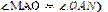 
.
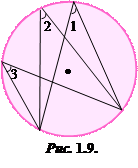
Вписаним у коло кутом називається кут, утворений двома хордами, що виходять з тієї самої точки на колі (рис.1.9). Вписаний кут вимірюється половиною дуги, на яку він спирається. Вписані кути, що спираються на ту саму дугу, між собою рівні. Вписаний кут, що спирається на півколо (на діаметр), прямий.
Кут з вершиною у центрі кола називається центральним кутом. Центральний кут, сторони якого перетинають коло у тих же точках, що і вписаного, називається відповідним центральним кутом до вписаного (рис. 1.10). Міра вписаного кута рівна половині міри відповідного центрального або доповнює його половину до 180°. Кут, утворений хордою і дотичною, яка проходить через кінець хорди, виміряється половиною дуги, що міститься між сторонами цього кута (рис. 1.11;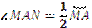 
). Кут, утворений двома хордами, що перетинаються всередині кола, виміряється півсумою двох дуг, одна з яких міститься між сторонами цього кута, а друга – між продовженнями цих сторін.
Кут, утворений двома дотичними, називається описаним (рис.1.8,в;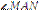 
). Описаний кут вимірюється піврізницею двох дуг, що містяться між його сторонами 
.
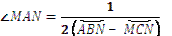Довжину кола шукають за формулою: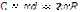 
, де d – діаметр кола, R – радіус кола, а довжину дуги кола – за формулою: 
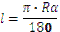, де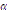 
– градусна міра відповідного центрального кута. Площа круга: 
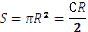, площа кругового сектора: , де R – радіус круга, 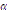– градусна міра відповідного центрального кута. Площа сегмента: 
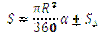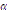, де – градусна міра центрального кута, який містить дугу цього кругового сегмента, а 
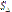– площа трикутника з вершинами в центрі круга й кінцях радіусів, що обмежують відповідний сектор. Знак «–» треба брати тоді, коли 
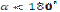, а знак « + » тоді, коли 
.
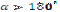Многокутники.
Многокутником називається проста замкнена ламана. Наприклад, многокутником А1А2…Аn називається лінія, яку отримують при послідовному сполученні n різних точок А1, А2, …, Аn відрізками так, щоб кожна точка була сполучена з наступною, а остання з першою (рис.1.12). Розрізняють многокутники плоскі й не плоскі. Плоский многокутник – частина площини, обмежена многокутником.
 |
Також будь-який многокутник може бути опуклим або не опуклим. Многокутник опуклий, якщо він лежить в одній півплощині відносно кожної прямої, що проходить через дві його сусідні вершини (рис.1.12, б, г, д).
Многокутники називають рівними, якщо вони при накладанні суміщаються. Для опуклого n – кутника сума внутрішніх кутів дорівнює 
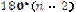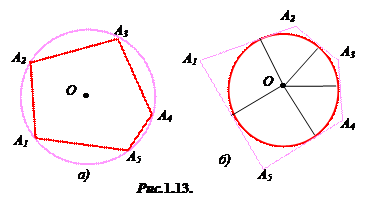
, а кількість діагоналей будь-якого n – кутника дорівнює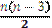 
. Якщо всі сторони опуклого многокутника рівні між собою і всі кути теж рівні між собою, то його називають правильним (рис. 1.12,д). Якщо всі вершини многокутника лежать на деякому колі, то він називається вписаним в це коло. Якщо сторони многокутника дотикаються до деякого кола, то він називається описаним навколо кола (рис.1.13). За кількістю сторін n – кутника, йому дають назву. Наприклад, трикутник (n = 3), чотирикутник (n = 4), п’ятикутник (n = 5) і т.д.
Як побудувати правильний n – кутник?
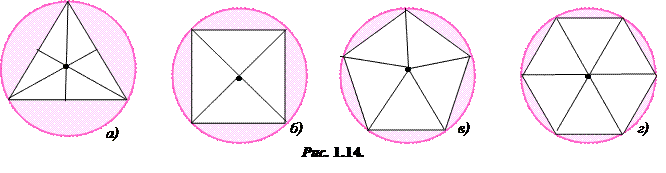
Якщо коло поділити на n рівних частин і точки послідовно сполучити відрізками, то дістанемо правильний n – кутник, вписаний у коло (рис. 1.14).
Якщо коло поділити на n рівних частин і через точки поділу провести дотичні до кола, то відрізки цих дотичних утворять правильний n – кутник описаний навколо кола (рис. 1.15).