1. Вибір геометричних понять, які називають основними поняттями (абстрактних фігур).
2. Формулювання основних властивостей для цих геометричних понять за допомогою тверджень, які вважаються істинними без доведень, як очевидні.
3. Побудова інших понять, які означуються через основні поняття та їх властивості, та інших тверджень, істинність яких встановлюється шляхом доведень, опираючись на відомі.
Така побудова науки називається аксіоматичною. Її назва походить від слова «аксіома». Це слово грецького походження, що в перекладі на українську мову означає «повага», «авторитет», «незаперечна істина». Аксіома – твердження, яке приймається без доведення. (У переносному значенні: «аксіома – це те твердження, яке внаслідок свого авторитету не викликає сумнівів»). Основні властивості найпростіших геометричних фігур, які не доводяться і є вихідними при доведенні інших властивостей називаються аксіомами геометрії.
Для шкільного курсу планіметрії визначено:
1. Основні геометричні фігури (поняття) – точка, пряма.
(Точка – найпростіша геометрична фігура. Всі інші геометричні фігури складаються з точок, у тому числі й пряма).
2. Аксіоми планіметрії – основні властивості найпростіших геометричних фігур.
3. Систему означень планіметричних фігур та теорем, що підтверджують їх властивості.
АКСІОМИ ПЛАНІМЕТРІЇ
| № п/п | Назва аксіоми | Зміст аксіоми | Наслідки з аксіом | |||
| І. | 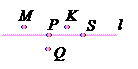 Аксіоми належності
І1. Аксіоми належності
І1.
І2. | І1.. Яка б не була пряма, існують точки, що належать цій прямій, і точки, що не належать їй. І2.. Через будь-які дві точки можна провести пряму і до того ж тільки одну. | Дві різні прямі або не перетинаються, або перетинаються тільки в одній точці. | |||
| ІІ. | Аксіоми розміщення
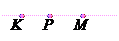 ІІ1. ІІ1.
 ІІ2. ІІ2.
| ІІ1. З трьох точок на прямій одна і тільки одна лежить між двома іншими. ІІ2. Пряма розбиває площину на дві півплощини. | Якщо кінці якого-небудь відрізка належать одній півплощині, то відрізок не перетинає пряму. Якщо кінці відрізка належать різним півплощинам, то відрізок перетинає пряму. | |||
| ІІІ. | Аксіоми вимірювання
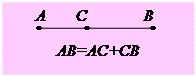 ІІІ1.
ІІІ2. ІІІ1.
ІІІ2.
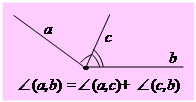
| ІІІ1. Кожний відрізок має певну довжину, більшу від нуля. Довжина відрізка дорівнює сумі довжин частин, на які він розбивається будь-якою його точкою. ІІІ2. Кожний кут має певну градусну міру, більшу від нуля. Розгорнутий кут дорівнює 180°. Градусна міра кута дорівнює сумі градусних мір кутів, на які він розбивається будь-яким променем, що проходить між його сторонами. | Якщо три точки А, В і С лежать на одній прямій, то точка В лежатиме між точками А і С, якщо АС = АВ+СВ. Якщо від даної півпрямої відкласти в одній півплощині два кути, то сторона меншого кута, відмінна від даної півпрямої, проходить між сторонами більшого кута. | |||
| IV. | Аксіоми відкладання
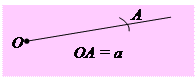 IV1.
IV2. IV1.
IV2.
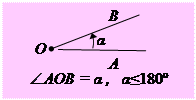
 IV3. IV3.
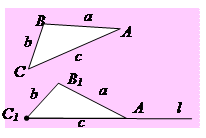
| IV1. На будь-якій півпрямій від її початкової точки можна відкласти відрізок даної довжини і тільки один. IV2. Від будь-якої півпрямої у даній півплощині можна відкласти кут з даною градусною мірою, меншою 180°, і тільки один. IV3. Який би не був трикутник, існує трикутник, що дорівнює йому у заданому розміщенні відносно даної пів прямої. | Якщо пряма, яка не проходить через жодну з вершин трикутника, перетинає одну з його сторін, то вона перетинає тільки одну з двох інших сторін. | |||
| V. | Аксіома паралельності
V.
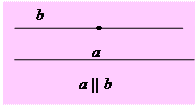
| V. Через точку, що не лежить на даній прямій, можна провести не більш як одну пряму, паралельну даній. | Якщо пряма перетинає одну з двох паралельних прямих, то вона перетинатиме й другу. |
До означуваних понять у геометрії відносять поняття відрізка, променя, трикутника та інші, оскільки для них існують пояснення «що це таке?» Наприклад.
 Нехай на прямій а задано дві різні точки А і В. Фігура, що складається з усіх точок прямої а, які лежать між точками А і В, включаючи точки А, В, називається відрізком (рис. 1.2). Точки А і В називаються кінцями відрізка, а всі інші точки – внутрішніми точками відрізка. Це означуване поняття називають означенням відрізка. Отже, означуваних понять багато.
Нехай на прямій а задано дві різні точки А і В. Фігура, що складається з усіх точок прямої а, які лежать між точками А і В, включаючи точки А, В, називається відрізком (рис. 1.2). Точки А і В називаються кінцями відрізка, а всі інші точки – внутрішніми точками відрізка. Це означуване поняття називають означенням відрізка. Отже, означуваних понять багато.
|
Щоб встановити правильність твердження про властивості тієї чи іншої геометричної фігури доводиться висловлювати деякі міркування. Серед цих міркувань є такі, які потребують доведення (теореми, задачі). Твердження, істинність якого встановлюється шляхом доведення і яке використовується часто для доведення інших тверджень, називається теоремою. Теорема складається з двох частин: умови і висновку. Для доведення теорем у шкільному курсі геометрії використовують в основному такі методи (§1.3):
а) по структурі доведення – прямий (аналітичний та синтетичний), від супротивного;
б) по використанню математичного апарату – алгебраїчний, координатний, векторний і т.д..
Всі міркування при доведенні теорем довільним методом опираються на аксіоми та відомі доведені факти. Тобто під час доведення теореми дозволяється користуватися тільки основними властивостями найпростіших фігур (аксіомами), і раніше доведеними властивостями (теоремами). Ніякими іншими властивостями фігур, навіть якщо вони нам здаються очевидними, користуватися не можна. Наприклад, при доведенні теорем можна користуватися рисунком. Однак це лише геометрична модель змісту тексту, вираженого словами. Тому робити за рисунком висновки про властивості фігур не дозволяється.
Отже, геометрія, як і інші математичні науки, будується за наступною схемою: спочатку потрібно ввести основні поняття, задати аксіоми (правила гри), а пізніше, опираючись на аксіоми, виводити інші факти (проводити гру за визначеними правилами, які є несуперечними між собою).

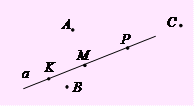 1.1°. Виберіть за рисунком два правильні математичні твердження.
1.1°. Виберіть за рисунком два правильні математичні твердження.
А) A 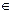 a; Б) M
a; Б) M 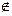 a; В) K
a; В) K 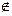 MP; Г) B
MP; Г) B 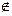 KP; Д) C
KP; Д) C 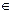 MP.
MP.
1.2°. На одній прямій позначено три точки А, В і С так, що АВ = 2,72 дм, ВС = 1,38 дм і АС = 1,34 дм. Визначте правильні твердження щодо розміщення однієї точки між двома іншими.
| А) А Î ВС; | Б) В Î АС; | В) С Î АВ; | Г) С Ï АВ; | Д) В Ï АС. |
1.3°. Відомо, що відрізок АМ довший за відрізок ВМ у 3 рази. Укажіть два математичні твердження, що відповідають тексту задачі.
А) АМ = 3 ВМ; В) АМ = 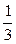 ВМ; Д) ВМ =
ВМ; Д) ВМ = 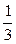 АМ .
АМ .
Б) 3 АМ = ВМ; Г) АМ + ВМ = 4 АМ;
1.4°. Укажіть два правильні скорочені записи умови задачі: «Відрізок АМ коротший за відрізок ВМ на 2 см».
А) АМ – ВМ = 2 см; В) АМ – 2 см = ВМ; Д) АМ = ВМ + 2 см .
Б) ВМ – АМ = 2 см; Г) АМ + 2 см = ВМ ;
1.5°. Знайдіть градусну міру кута 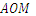 , якщо
, якщо 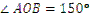 , а
, а 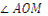 у 2 рази більший за
у 2 рази більший за 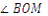 (М – внутрішня точка кута
(М – внутрішня точка кута 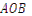 ).
).
А) 50°; Б) 100°; В) 75°; Г) 30°; Д) 120°.
1.6°. Знайдіть довжини відрізків АМ і ВМ (М Î АВ), якщо довжина відрізка АВ дорівнює 12 см, а відрізок АМ коротший, ніж відрізок ВМ на 3 см.
А) 1,5 см і 4,5 см; В) 7,5 см і 10,5 см;
Б) 4,5 см і 7,5 см; Г) 6 см і 9 см; Д) 5 см і 7 см.
1.7°°. На одній прямій позначили 21точку так, що відстань між будь-якими двома сусідніми точками дорівнює 3 см. Знайдіть відстань між крайніми точками.
А) 63 см; Б) 60 см; В) 66 см; Г) 57 см; Д) 54 см.
1.8°°. На відрізку АВ, довжина якого 42 см, позначено точку М відповідно до умов (А – Д). Доберіть до кожної з них правильні твердження (1– 6).
 А) АМ > ВМ на 2 см; 1) АМ = 18 см;
А) АМ > ВМ на 2 см; 1) АМ = 18 см;
Б) АМ < ВМ на 6 см; 2) ВМ = 28 см;
В) 2АМ = ВМ; 3) АМ = 22 см;
Г) АМ : ВМ = 3 : 4; 4) ВМ = 24 см;
Д) 0,5 ВМ = АМ. 5) АМ = 14 см;
6) ВМ = 20 см;
1.9°°. Промінь ОА проходить між сторонами кута РОМ , градусна міра якого дорівнює 160°. Доберіть до кожної умови (А – Д) правильне твердження (1 – 6).
 А) Ð РОА > Ð АОМ на 40°; 1) Ð АОМ = 110°;
А) Ð РОА > Ð АОМ на 40°; 1) Ð АОМ = 110°;
Б) Ð РОА < Ð АОМ на 60°; 2) Ð АОР = 120°;
В) Ð АОМ = 0,6 Ð АОР; 3) Ð МОА = 60°;
Г) Ð АОР = 3 Ð АОМ; 4) Ð РОА = 100°;
Д) Ð АОМ : Ð РОА = 3 : 5. 5) Ð АОМ = 40°;
6) Ð РОА = 50°.