1 / 2 1 2 следующая > >>

Арифметические действия и их свойства

Дата: 2025-04-30; Просмотры: 2

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Арифметика и алгебра

Арифметика – раздел математики, изучающий числа, выраженные цифрами, их отношения, свойства и действия с ними.

Алгебра – раздел математики, в котором вместе с цифрами используются буквы и буквенные выражения.

Натуральные числа – числа, получившиеся в результате счета. 1,2,3,4,5,6,7,8,9,10,11…

0 не является натуральным числом.

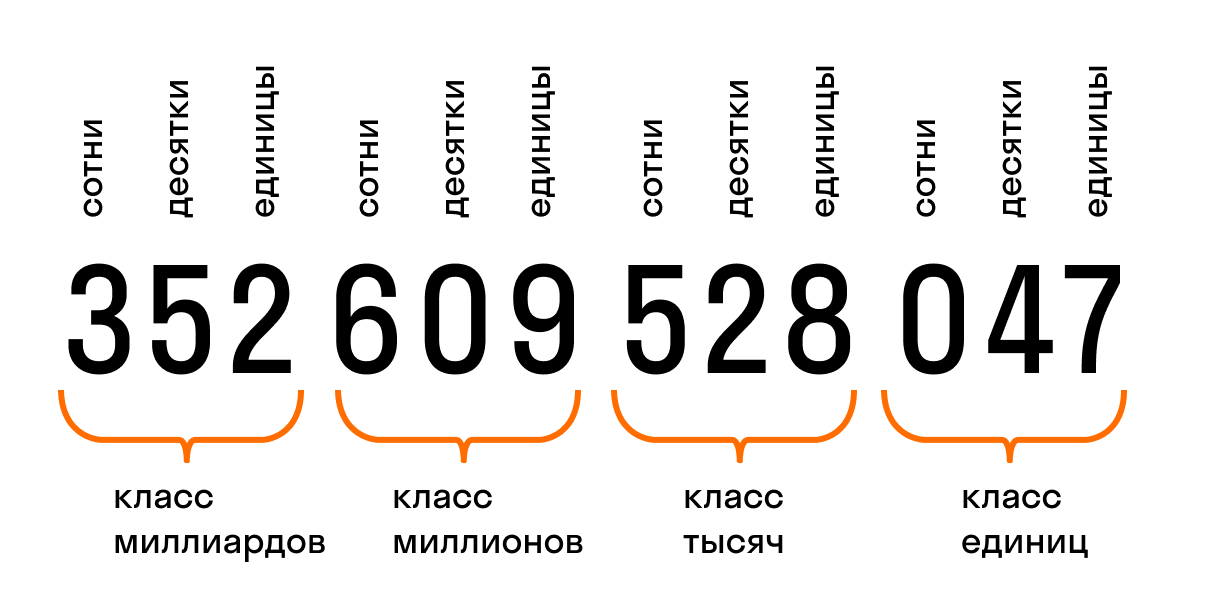
Сумма разрядных слагаемых — это запись многозначного числа в виде сложения количеств его разрядных единиц

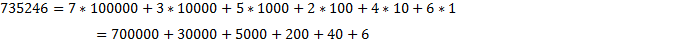
Арифметические действия и их свойства

Сложение: слагаемое + слагаемое = сумма

Вычитание: уменьшаемое - вычитаемое = разность

Умножение: множитель * множитель = произведение

Деление: делимое : делитель = частное

Арифметические действия

Сложение

Вычитание

Умножение

Деление

a+b+c=b+a+c

(a+b)+c=a+(b+c)

a+0=a

a-0=a

a-a=0

a-(b+c)=(a-b)-c

(a+b)-c=(a-с)+b

a×0=0

a×1=a

abc=bca

(ab)c=a(bc)

a(b+c)=ab+ac

a(b-c)=ab-ac

a:0=нельзя

0:a=0

a:a=1

a:1=a

Степень числа

a^x=a×a×…×a

_{x раз}

Деление с остатком – разделить с остатком натуральное число a на число b, значит, найти такие числа q и r, чтобы выполнялось равенство: a = b * q + r , r < b, где a – делимое, b – делитель, q – неполное частное, r – остаток.

23:4=5(ост 3) 23=5*4+3

Нахождение неизвестных:

Уравнение – алгебраическое равенство, содержащее одно или несколько неизвестных, обозначенных буквами.

Решить уравнение – найти все корни уравнения или убедиться, что их нет.

Корень уравнения – число, при подстановке которого вместо неизвестного получается верное числовое равенство.

Чтобы найти Слагаемое нужно из суммы вычесть разность.

Уменьшаемое – к разности прибавить вычитаемое.

Вычитаемое – из уменьшаемого вычесть разность.

Множитель – произведение разделить на другой множитель.

Делимое – частное умножить на делитель.

Делитель – делимое разделить на частное.

Порядок действий:

1. Возведение в степень.

2. Умножение и деление

3. Сложение и вычитание

Если есть скобки, то сначала выполняют действия в скобках, учитывая порядок выше, а потом действия вне скобок.

Делители и кратные

Натуральное число m делится на натуральное число n, если существует натуральное число p такое, что m = n * p .

n – делитель числа m, а m – кратное числа n.

Делители числа 18: 1, 2, 3, 6, 9, 18.

Кратные числа 18: 18, 36, 54, 72 и т.д.

Простое число – натуральное число, не равное 1, которое имеет только два делителя: 1 и само себя.

Таблица простых чисел до 1000

2	3	5	7	11	13	17	19	23	29	31	37	41	43	47	53	59	61
67	71	73	79	83	89	97	101	103	107	109	113	127	131	137	139	149	151
157	163	167	173	179	181	191	193	197	199	211	223	227	229	233	239	241	251
257	263	269	271	277	281	283	293	307	311	313	317	331	337	347	349	353	359
367	373	379	383	389	397	401	409	419	421	431	433	439	443	449	457	461	463
467	479	487	491	499	503	509	521	523	541	547	557	563	569	571	577	587	593
599	601	607	613	617	619	631	641	643	647	653	659	661	673	677	683	691	701
709	719	727	733	739	743	751	757	761	769	773	787	797	809	811	821	823	827
829	839	853	857	859	863	877	881	883	887	907	911	919	929	937	941	947	957
953	971	977	989	991	997

Составное число – натуральное число, которое имеет более двух делителей.

Четное число – число, которое делится на 2 без остатка.

Нечетное число – число, которое делится на 2 с остатком.

Признаки делимости натуральных чисел:

Число делится на	2	Если последняя цифра числа четная (делится на 2) или 0
	3	Если сумма цифр делится на 3
	4	Если две последние цифры числа делятся на 4 без остатка
	5	Если последняя цифра 0 или 5
	6	Если число делится на 2 и на 3
	8	Если три последние цифры нули или образуют число, делящееся на 8
	9	Если сумма цифр числа делится на 9
	10	Если последняя цифра числа 0
	11	Если сумма цифр на нечетных позициях равна сумме цифр на четных позициях
	25	Если последние две цифры числа 00, 25, 50, 75

Разложить число на простые множители – представить это число в виде произведения простых чисел.

360	2
180	2
90	2
45	5
9	3
3	3
1

360=2*2*2*5*3*3=2³*5*3²

Наибольшие общий делитель (НОД) чисел – наибольшее число, на которое без остатка делится каждое из этих чисел.

Делители 16: 1, 2, 4, 8, 16.

Делители 20: 1, 2, 4, 5, 10, 20.

Общие делители 16 и 20: 1, 2, 4.

НОД(16;20)=4.

Числа, которые не имеют общих делителей, кроме 1, называются взаимно простыми.

Чтобы найти НОД нескольких чисел нужно:

1. Разложить эти числа на простые множители.

2. Перемножить общие множители всех этих чисел, взяв каждый из них с наименьшим показателем степени.

48	2	360	2	48=22223=2⁴*3
24	2	180	2	360=222335=2³3²*5
12	2	90	2	Наименьший показатель степени для 2 – 3, для 3 – 1
6	2	45	3	(степень 1 можно не писать)
3	3	15	3	НОД(48,360)=2223=2³3=24
1		5	5
		1

Наименьшее общее кратное (НОК) нескольких чисел – это наименьшее число, которое делится без остатка на каждое из данных чисел.

НОК(3; 9; 27) = 27

Чтобы найти НОК нескольких чисел нужно:

1. Разложить числа на простые множители.

2. Найти произведение всех получившихся простых множителей, взяв каждый из них с наибольшим показателем степени.

40	2	64	2	112	2	40=2³*5
20	2	32	2	56	2	64=2⁶
10	2	16	2	28	2	112=2⁴*7
5	5	8	2	14	2	Наибольший показатель степени для 2 – 6,
1		4	2	7	7	для 5 и 7 – 1 (степень 1 можно не писать)
		2	2	1		НОК(40; 64; 112)=2⁶57=2240
		1

НОК взаимно простых чисел равен их произведению.

НОК(6; 13)=6*13=78

Обыкновенные дроби

Обыкновенная дробь – выражение вида 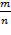(или m / n). Знаменатель (n) показывает, на сколько равных частей разделили целое, а числитель (m) показывает, сколько таких частей (долей) взяли.

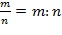
Правильная дробь – дробь, у которой числитель меньше знаменателя.

Смешанная дробь – дробь, у которой есть целая и дробная часть.

Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же число, не равное 0, то получится дробь, равная данной.

Сократить дробь – разделить и числитель, и знаменатель на одно и то же число, не равное 1.

Привести к общему знаменателю – найти такой знаменатель, который делится нацело на знаменатели обеих дробей.

Сравнение дробей

1. Если одинаковый знаменатель, то больше та, у которой числитель больше.

2. Если одинаковый числитель, то больше та, у которой знаменатель меньше.

3. Если и числитель, и знаменатель разные, то нужно привести к общему знаменателю и сравнить по правилу а.

Арифметические действия с дробями:

1. Сложение и вычитание – привести дробь к общему знаменателю, числитель сложить/вычесть, знаменатель оставить без изменений. Для смешанной дроби: или перевести дробь в неправильную, или целая часть + целая, дробная + дробная.

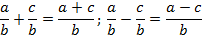
2. Умножение – числитель умножается на числитель, а знаменатель на знаменатель.

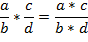
3. Деление – это умножение на дробь, обратную делителю, т.е. нужно в делителе числитель и знаменатель поменять местами.

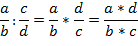
Найти дробь от числа – умножить число на дробь.

Найти число по значению дроби – разделить значение на дробь.

Десятичные дроби

Десятичная дробь – дробь, знаменателем которой является разрядная единица (10, 100, 1000, 10000, 100000 и т.д.). Записывается в виде целой и дробной части, разделенными запятой.

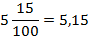
Количество знаков после запятой соответствует количеству нолей в знаменателе.

Если дописать в конце десятичной дроби 0 (один или несколько) или убрать, нули, на которые она оканчивается, то получится дробь равная данной.

2,57=2,570 3,4570=3,457

1 / 2 1 2 следующая > >>

2	3	5	7	11	13	17	19	23	29	31	37	41	43	47	53	59	61
67	71	73	79	83	89	97	101	103	107	109	113	127	131	137	139	149	151
157	163	167	173	179	181	191	193	197	199	211	223	227	229	233	239	241	251
257	263	269	271	277	281	283	293	307	311	313	317	331	337	347	349	353	359
367	373	379	383	389	397	401	409	419	421	431	433	439	443	449	457	461	463
467	479	487	491	499	503	509	521	523	541	547	557	563	569	571	577	587	593
599	601	607	613	617	619	631	641	643	647	653	659	661	673	677	683	691	701
709	719	727	733	739	743	751	757	761	769	773	787	797	809	811	821	823	827
829	839	853	857	859	863	877	881	883	887	907	911	919	929	937	941	947	957
953	971	977	989	991	997

2	3	5	7	11	13	17	19	23	29	31	37	41	43	47	53	59	61
67	71	73	79	83	89	97	101	103	107	109	113	127	131	137	139	149	151
157	163	167	173	179	181	191	193	197	199	211	223	227	229	233	239	241	251
257	263	269	271	277	281	283	293	307	311	313	317	331	337	347	349	353	359
367	373	379	383	389	397	401	409	419	421	431	433	439	443	449	457	461	463
467	479	487	491	499	503	509	521	523	541	547	557	563	569	571	577	587	593
599	601	607	613	617	619	631	641	643	647	653	659	661	673	677	683	691	701
709	719	727	733	739	743	751	757	761	769	773	787	797	809	811	821	823	827
829	839	853	857	859	863	877	881	883	887	907	911	919	929	937	941	947	957
953	971	977	989	991	997

2	3	5	7	11	13	17	19	23	29	31	37	41	43	47	53	59	61
67	71	73	79	83	89	97	101	103	107	109	113	127	131	137	139	149	151
157	163	167	173	179	181	191	193	197	199	211	223	227	229	233	239	241	251
257	263	269	271	277	281	283	293	307	311	313	317	331	337	347	349	353	359
367	373	379	383	389	397	401	409	419	421	431	433	439	443	449	457	461	463
467	479	487	491	499	503	509	521	523	541	547	557	563	569	571	577	587	593
599	601	607	613	617	619	631	641	643	647	653	659	661	673	677	683	691	701
709	719	727	733	739	743	751	757	761	769	773	787	797	809	811	821	823	827
829	839	853	857	859	863	877	881	883	887	907	911	919	929	937	941	947	957
953	971	977	989	991	997