1.3.17. Базисные функции комплексной формы ряда Фурье

Дата: 2025-06-02; Просмотры: 10

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

* ; # ; # ; #

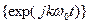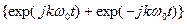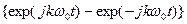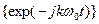
1.3.18. Спектральная плотность амплитуд непериодического сигнала 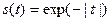равна:

* 2/(1+w²); # 1/(1+w²); # 1/w²; # 1/(2+w²); #1/t;

1.3.19. Базисные функции ряда Котельникова

* ; # ; # ; #

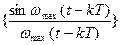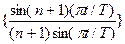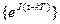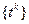
1.3.20. Спектральная плотность амплитуд непериодического сигнала 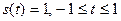, равна:

* 2sin(w)/w; # sin(w)/w; # cos(w)/w; # sin²(w)/w²

1.3.21. Спектральная плотность амплитуд сигнала: 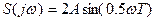. Ширина спектра в герцах, для которой эта функция первый раз обращается в ноль, равна

* 1/Т; # 2/Т; # 3/Т; # p/Т; # 2p

1.3.22. Для выбранного базиса ортогональных функций 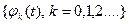, обобщенный ряд Фурье определяется соотношением

* ; # ; # ; #

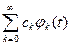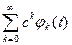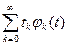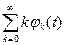
1.3.23. Для выбранного базиса ортонормальных функций 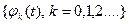, коэффициенты разложения сигнала s(t) в обобщенный ряд Фурье определяются по соотношению

* ; # ; # ; #

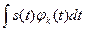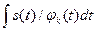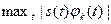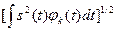
Тесты по теме 5.1: «Модели непрерывных каналов связи».

5.1.1. На вход канала связи с коэффициентом передачи К(f)=1; 0<f<F; поступает белый шум с постоянной спектральной плотностью мощности G₀. Мощность шума на выходе канала связи

* FG₀; # G₀; # 2FG₀; # 2pF; # pG₀/F

5.1.2. На вход канала связи с коэффициентом передачи К(f)=2; 0<f<F; поступает белый шум с постоянной спектральной плотностью мощности G₀. Дисперсия шума на выходе канала связи

* 4FG₀; # FG₀; # 2FG₀; # 2pF; # pG₀/F

5.1.3. На вход канала связи с коэффициентом передачи К(f)=0.1; 0<f<F; поступает белый шум с постоянной спектральной плотностью мощности G₀. Дисперсия шума на выходе канала связи

* 0.01FG₀; # FG₀; # 2FG₀; # 2pG₀F; # pG₀/F

5.1.4. Соответствие входного и выходного сигналов непрерывного канала связи

* аналоговый – аналоговый; # аналоговый – дискретный; # дискретный – аналоговый

5.1.5. Канал связи, для которого справедлив принцип суперпозиции и не происходит обогащение спектра отклика по сравнению со спектром воздействия,

* линейный; # линейно-параметрический; # нелинейный; # нелинейно-параметрический

5.1.6. Канал связи, для которого справедлив принцип суперпозиции и происходит обогащение спектра отклика по сравнению со спектром воздействия,

* линейно-параметрический; # линейный; # нелинейный; # нелинейно-параметрический

5.1.7. Канал связи, для которого не справедлив принцип суперпозиции и происходит обогащение спектра отклика по сравнению со спектром воздействия,

* нелинейный; # линейно-параметрический; # линейный; # нелинейно-параметрический

5.1.8. Канал связи, в котором действует аддитивная помеха типа «белого шума» с нормальным законом распределения мгновенных значений,

* гауссовский; # релеевский; # райсовский; # марковский

5.1.9. На вход канала связи, в котором действует шум с мощностью 10 (В²), поступает сигнал с мощностью 100 (В²). Отношение сигнал шум в канале

* 10 дБ; # 20 дБ; # 1 дБ; # 100 дБ; # 0 дБ

5.1.10. На вход канала связи, в котором действует шум с мощностью 1 (В²), поступает сигнал с мощностью 1 (В²). Отношение сигнал шум в канале

* 0 дБ; # 20 дБ; # 1 дБ; # 100 дБ; # 10 дБ

5.1.11. На вход канала связи, в котором действует шум с мощностью 0.1 (В²), поступает сигнал с мощностью 100 (В²). Отношение сигнал шум в канале

* 30 дБ; # 20 дБ; # 1 дБ; # 10 дБ; # 0 дБ

5.1.12. В аддитивном канале связи дисперсии сигнала и шума складываются, если сигнал и шум _____ случайные процессы

* независимые; # равноправные; # произвольные; # одинаковые

5.1.13. В аддитивном канале связи и сигнал и шум гауссовские случайные процессы. Отклик канала связи является

* гауссовским; # релеевским; # райсовским; # марковским

5.1.14. В аддитивном канале связи и сигнал и шум независимые случайные процессы с дисперсиями 19 (В²) и 6 (В²). Дисперсия отклика канала связи

* 25; # 13; # 19; # 6; # 5

5.1.15. В системе электросвязи помеха, перемножаемая с сигналом, является

* мультипликативной; # аддитивной; # переходной; # анимационной

5.1.16. На вход канала связи с коэффициентом передачи К(f)=0,4 ; 0<f<F; поступает сигнал со спектральной плотностью мощности: 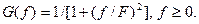Мощность сигнала на выходе канала связи

* 0.04pF; # 4pF; # F; # 2pF; # pF

5.1.17. Селективные замирания сигнала вызываются изменением в канале связи

* коэффициента передачи; # аддитивного шума; # чувствительности приемника

5.1.18. На вход канала связи с коэффициентом передачи К(f)=f/F; 0<f<F; поступает белый шум с постоянной спектральной плотностью мощности G₀. Дисперсия шума на выходе канала связи

* G₀F/3 ; # FG₀/5; # 2FG₀; # pG₀F2/2; # pG₀/F

5.1.19. Связь выхода и входа непрерывного канала связи определяется соотношением: 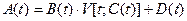. Соответствие между сигналами и их наименованиями

* A(t) - отклик канала; * B(t) - мультипликативная помеха; * V(t) - полезная составляющая отклика; * C(t) - входное воздействие; * D(t) - аддитивная помеха

5.1.20 На вход канала связи с коэффициентом передачи К(f)=[f/F]² ; 0<f<F; поступает белый шум с постоянной спектральной плотностью мощности G₀. Дисперсия шума на выходе канала связи

* G₀F/5 ; # FG₀/3; # 2FG₀; # pG₀F/3; # pG₀/F

5.1.21. На вход канала связи с коэффициентом передачи К(f)=2 ; 0<f<F; поступает сигнал со спектральной плотностью мощности: 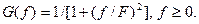Мощность сигнала на выходе канала связи

* pF; # F/2; # F; # 2pF; # 4p/F

5.1.22. На вход канала связи с коэффициентом передачи К(f)=4 ; 0<f<F; поступает сигнал со спектральной плотностью мощности: 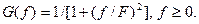Мощность сигнала на выходе канала связи

* 4pF; # F/2; # F; # 2pF; # pF

5.1.23 На вход канала связи с коэффициентом передачи 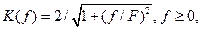поступает белый шум с постоянной спектральной плотностью мощности G₀. Дисперсия шума на выходе канала связи

* 2pFG₀; # FG₀; # 2FG₀; # 2pF; # pG₀/F

5.1.24. На вход канала связи с единичной АЧХ в полосе частот [0; F] поступает сигнал со спектральной плотностью мощности: 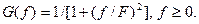Мощность сигнала на выходе канала связи

* pF/4; # F/2; # F; # 2pF; # 4p/F

5.1.25. На вход канала связи с коэффициентом передачи 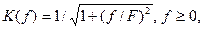поступает белый шум с постоянной спектральной плотностью мощности G₀. Дисперсия шума на выходе канала связи

* pFG₀/2; # FG₀; # 2FG₀; # 2pF; # pG₀/F

5.1.26. Двоичный источник вырабатывает равновероятные символы. Двоичный ДКС характеризуется матрицей переходных вероятностей с элементами: p(0|0) = 0.5, p(1|0) = 0.5, p(0|1) = 0.3, p(1|1) = 0.7. Средняя вероятность ошибки

* 0.4; # 0.3; # 0.45; # 0.6

5.1.27. Двоичный источник вырабатывает равновероятные символы. Двоичный ДКС характеризуется матрицей переходных вероятностей с элементами: p(0|0) = 0.8, p(1|0) = 0.2, p(0|1) = 0.4, p(1|1) = 0.6. Средняя вероятность ошибки

* 0.3; # 0.25; # 0.4; # 0.1

5.1.28. Двоичный источник вырабатывает равновероятные символы. Двоичный ДКС характеризуется матрицей переходных вероятностей с элементами: p(0|0) = 0.8, p(1|0) = 0.2, p(0|1) = 0.3, p(1|1) = 0.7. Средняя вероятность ошибки

* 0.25; # 0.3; # 0.45; # 0.1

5.1.29. Двоичный источник вырабатывает равновероятные символы. Двоичный ДКС характеризуется матрицей переходных вероятностей с элементами: p(0|0) = 0.6, p(1|0) = 0.4, p(0|1) = 0.3, p(1|1) = 0.7. Средняя вероятность ошибки

* 0.35; # 0.2; # 0.45; # 0.1

5.1.30. В двоичном симметричном ДКС: p(1|0) = p(0|1) = p; p(0) = 0.5. Средняя вероятность ошибки

* p; # 0.5; # 0.5p; # 2p

Тесты по теме 1.4. «Дискретизация сигналов во времени»

S : Из фрагментов текста составьте правильную формулировку теоремы Котельникова.

1: Непрерывная функция, не содержащая

2: частот выше F,

3: полностью определяется

4: своими отсчетами, взятыми

5: через интервал

6: времени .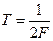

S : Из фрагментов текста составьте правильную формулировку процесса восстановления непрерывного сигнала.

1: Для восстановления непрерывной

2: функции из импульсов-отсчетов

3: необходимо подать их

4: на вход

5: идеального ФНЧ.

6: на выход

S : Из фрагментов текста составьте правильное утверждение.

1: Теорема Котельникова

2: справедлива с погрешностью

3: равной нулю для

4: процесса с финитным

5: спектром.

S : Из фрагментов текста составьте правильное утверждение.

1: Теорема Котельникова

2: справедлива с погрешностью

3: не равной нулю для

4: процесса с бесконечным

5: спектром.

Тесты по теме 1.3. «Разложение сигналов в обобщенный ряд Фурье»

S : Из фрагментов текста составьте правильное утверждение.