1 / 5 1 2 3 4 5

1.1.23. Функция плотности вероятностей пуассоновского сигнала

Дата: 2025-06-02; Просмотры: 11

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Тесты по теме 1.1: Классификация сигналов и помех.

Тесты по теме 1.2: Функциональные пространства и их базисы.

1.1.1. Наименование помехи, которая перемножается с сигналом:

* мультипликативная; # аддитивная; # комбинированная ;

1.1.2. Наименование помехи, которая суммируется с сигналом:

* аддитивная; # мультипликативная; # комбинированная ;

1.1.3. Сигнал, непрерывно изменяющийся и по аргументу и по значению,

* аналоговый; # дискретно-аналоговый; # аналого-дискретный; # цифровой

1.1.4. Структурная схема передатчика системы связи содержит блоки:

* Источник сообщения, кодер, модулятор, генератор переносчика, выходное устройство. # Источник сообщения, кодер, модулятор, генератор переносчика, демодулятор.

# Источник сообщения, декодер, модулятор, генератор переносчика, выходное устройство.

# Источник сообщения, кодер, демодулятор, генератор переносчика, выходное устройство.

# Источник сообщения, кодек, модулятор, генератор переносчика, выходное устройство.

1.1.5. Структурная схема приемника системы связи содержит блоки:

* Входное устройство, демодулятор, декодер, получатель сообщения.

# Выходное устройство, модулятор, декодер, получатель сообщения.

# Входное устройство, демодулятор, кодер, получатель сообщения.

# Входное устройство, демодулятор, кодек, получатель сообщения.

# Входное устройство, модем, декодер, получатель сообщения.

1.1.6. Сигнал, изменяющийся дискретно и по аргументу и по значению,

* цифровой; # дискретно-аналоговый; # аналого-дискретный; # аналоговый

1.1.7. Периодические сигналы

* ; * ; # ; # ; #

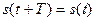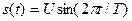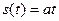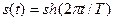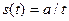
1.1.8. Шумы и помехи в канале связи представляют собой ____ процессы.

* случайные; # полезные; # детерминированные; # регулярные

1.1.9. Сигналы, значения которых можно предсказать с вероятностью 1:

* детерминированные; # квазидетерминированные; # случайные; # шумовые

1.1.10. Сигналы, значения которых нельзя предсказать точно:

* стохастические; # детерминированные; # неслучайные; # достоверные

1.1.11. Модулятор и демодулятор образуют:

* модем; # кодер; # декодер; # кодек; # источник сообщения.

1.1.12. Спектральная плотность мощности белого шума -

* равномерная; # периодическая; # непостоянная; # импульсная

1.1.13. Кодер и декодер образуют:

* кодек; # модулятор; # демодулятор; # модем; # источник сообщения.

1.1.14. Операцию детектирования осуществляет:

* детектор; # модулятор; # кодер; # декодер; # фильтр.

1.1.15. Аналитическое выражение для сигнала АМ следующее:

* u(t)= 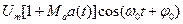; # u(t)= ;

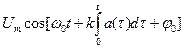# u(t)= 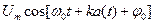; # u(t)=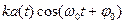

1.1.16. Взаимосвязь между шириной спектра D f и центральной частотой f₀узкополосного сигнала

* D f << f₀; # D f = f₀; # D f > f₀; # D f >> f₀;

1.1.17. Значения случайного процесса некоррелированы, если они ____

* независимы; # нелинейны; # зависимы; #ненаблюдаемы; # неоднозначны.

1.1.18. Дисперсии складываются при сложении ___ случайных процессов

* независимых; # одинаковых; # зависимых; # произвольных; # равнозначных.

1.1.19. Случайный сигнал стационарен, если его статистические характеристики не зависят ____

* от начального момента времени; # от его предыстории; # от его значений в текущий момент; # от его значений в будущем

1.1.20. Случайный сигнал стационарен в широком смысле, если от начального момента времени не зависят его моменты ____

* первого и второго порядков; # произвольного порядка; # центральные; # начальные

1.1.21. Эргодический случайный сигнал является ____ случайным процессом

* стационарным; # нестационарным; # детерминированным; # неинформативным

1.1.22. Функция плотности вероятностей гауссовского сигнала

* ; # ; # ; #

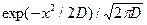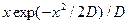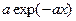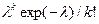
1.1.23. Функция плотности вероятностей пуассоновского сигнала

* ; # ; # ; #

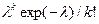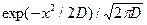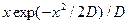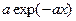
1.1.24. Одномерные законы распределения вероятностей дискретных случайных сигналов

* ; * ; # ; # ; #

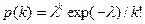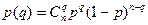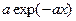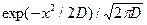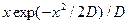
1.1.25. Одномерные функции плотности вероятностей непрерывных случайных сигналов

* ; * ; # ; # ;

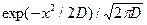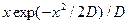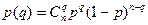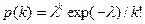1.2.1. Метрическое пространство сигналов – это множество сигналов, для которого подходящим образом определено ____.

* расстояние; # разбиение; # отношение; # соответствие.

1.2.2. Евклидова норма вектора (3,3,3,3)

* 6; # 1; # 2; # 3

1.2.3. Множество векторов 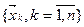, обладающее свойством: 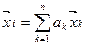, образует ____ пространство

* линейное; # полное; # параметрическое; # метрическое

1.2.4. Базисные вектора 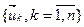Евклидова пространства линейно-независимы, если равенство: 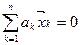, справедливо только при всех a_k, равных:

* 0; # 1; # ¥; # -1.

1.2.5. Евклидова норма вектора (2, 2, 2, 2)

* 4; # 1; # 2; # 1/2

1.2.6. Линейное n-мерное пространство с базисом 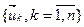имеет ____ разложение вида: ,

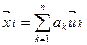* единственное; # произвольное; # ограниченное; # (n+1);

1.2.7. Евклидова норма вектора (1, 1, 1, 1)

* 2; # 1; # 4; # 1/2

1.2.8. Гильбертова норма сигнала x(t) = 1, tÎT,

* T⁰^.5; # T; # T²; # 1

1.2.9. Евклидово расстояние между векторами: (2, 2, 2, 2) и (1, 1, 1, 1)

* 2; # 1/2; # 3; # 1

1.2.10. Гильбертово расстояние между сигналами x(t) = 1 и y(t) = 2, tÎT,

* T⁰^.5; # 1; # T²; # T

1.2.11. По аналогии с 3-х мерным физическим пространством, элементы n-мерного линейного представляют собой

* векторы; * точки; # линии; # кривые; # функции

1.2.12. В линейном пространстве система линейно-независимых векторов образует

* базис; # базу; # основу; # фундамент

1.2.13. Аналогом длины вектора в линейном пространстве сигналов служит ____

* норма; # база; # метрика; # линия

1.2.14. Скалярное произведение векторов (1, 1, 1, 1, 1, 1) и (1, -1, 1, -1, 1, -1) равно:

* 0; # 1; # 2; # 4; # 6

1.2.15. Условие квадратичной интегрируемости сигнала x(t)

* ; # ; # ; #

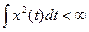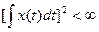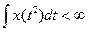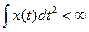
1.2.16. Скалярное произведение векторов 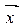и 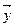Евклидова пространства

* ; # ; # ; #

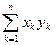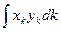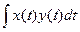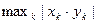
1.2.17. Скалярное произведение векторов 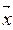и 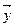Гильбертова пространства

* ; # ; # ; #

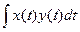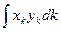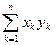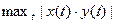
1.2.18. Норма вектора 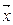Евклидова пространства

* ; # ; # ; #

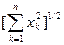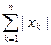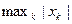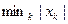
1.2.19. Норма вектора 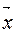Гильбертова пространства

* ; # ; # ; #

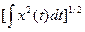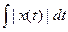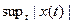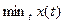
1.2.20. Расстояние между векторам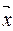и и 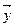Евклидова пространства

* ; # ; # ; #

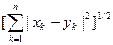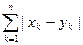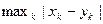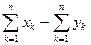
1.2.21. Расстояние между векторам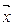и и 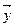Гильбертова пространства

* ; # ; # ; #

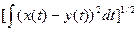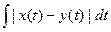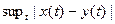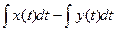
1.2.22. Условие ортогональности векторов Евклидова пространства

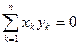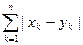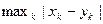* ; # =0; # 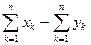=0; # =0

1.2.23. Условие ортогональности векторов Гильбертова пространства

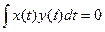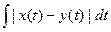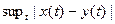* ; # =0; # 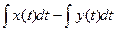=0; # =0

Тесты по теме 1.4. «Дискретизация сигналов во времени»

1.4.1. Спектр непрерывной функции, которая полностью определяется своими отсчетами, взятыми в моменты времени kT, T=1/2F_m :

* не содержит частот выше F_m;

# содержит частоты выше F_m;

# бесконечный;

# не содержит частот меньше F_m;

1.4.2. Интервал дискретизации по теореме Котельникова для сигнала, спектр которого ограничен частотой F _m , равен:

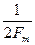* ; #1/F_m; # F_m; #2/ F_m; # 2 F_m

1.4.3. Интервал дискретизации по теореме Котельникова для сигнала, спектр которого ограничен частотой ω _m , равен :

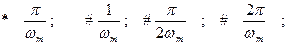
1.4.4. Интервал дискретизации, если спектр сигнала ограничен частотой 500 Гц, равен :

* 1мс ; # 2мс; # 500 мс; # 1000 Гц; #500 Гц.

1.4.5. Интервал дискретизации, если спектр сигнала ограничен частотой 3140 рад/с равен:

* 1 мс; # 2 мс; # 0.5 мс; # 1570 рад/с;

1.4.6. Фамилия автора теоремы, в соответствии с которой осуществляется дискретизация функции по времени:

* Котельников; # Винер; # Шеннон; # Фурье; #Лаплас.

1.4.7. Интервал дискретизации, если частота дискретизации 100 Гц, равен :

* 10мс ; # 20 mс; # 100 mс; # 50 Гц; # 10Гц.

1.4.8. Частота дискретизации, если интервал дискретизации 1мс, равна:

* 1000 Гц ; # 500 Гц; # 250 Гц; # 125 Гц;

1.4.9. Спектр сигнала, для которого интервал дискретизации

равен 10мс, ограничен частотой :

* 50 Гц ; # 100 Гц ; # 10мс; # 50 мс ; # 50 рад/с;

1.4.10. В соответствии с теоремой Котельникова осуществляется _____________ непрерывной функции.

* дискретизация ; # квантование; # усиление; # ослабление;

1.4.11. Для определения интервала дискретизации по теореме Котельникова должна быть задана ________ спектра функции.

* ширина; # высота; # длительность; # полнота;

1.4.12. Сигнал описывается функцией времени u(t)=cos2πt . Отсчеты сигнала, взятые в соответствии с теоремой Котельникова в моменты

времени t=0.5k, k=0,1,2, равны , соответственно:

* 1; -1; 1; # 1; 0; 1; # 1; 1; 1; # 0; 1; 0;

1.4.13. Сигнал описывается функцией времени u(t)=cosπt . Отсчеты сигнала, взятые в соответствии с теоремой Котельникова в моменты времени t=0.5k, k=0,1,2, равны , соответственно :

* 1; 0; -1; # 1; 0; 0; # 1;1;1; #0;1;0;

1.4.14. По теореме Котельникова отсчеты функции берутся с частотой, которую называют частотой ______________.

* дискретизации; # квантования; # усиления; # гармоники ;

1.4.15. Ряд Котельникова для непрерывной функция с заданной точностью может быть представлен в виде:

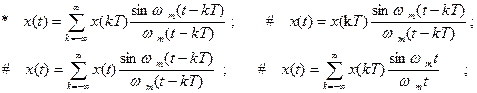
1.4.16. Для восстановления исходной непрерывной функции по ее отсчетам необходимо подать эти отсчеты на вход:

* идеального ФНЧ; # ФНЧ;

# резонансного контура; # RC фильтра;

1.4.17. Спектр сигнала ограничен частотой 1000 Гц. Интервал дискретизации в мкс и частота дискретизации в р/с, соответственно, равны:

* 500 мкс; 12560 рад/с; # 1000 мкс; 2000 рад/с;

# 500 мкс; 6280 рад/с; # 1000 мкс; 12560 рад/с;

1.4.18. Спектр сигнала ограничен частотой 6280 рад/с. Интервал дискретизации в мкс и частота дискретизации в кГц, соответственно, равны:

* 500 мкс; 2 кГц; # 1000 мкс; 2кГц;

# 500 мкс; 6280 рад/с; # 1000 мкс; 12560 рад/с;

1.4.19. Для восстановления непрерывной функции из отсчетов используется

______________ ФНЧ.

* идеальный ; # реальный; # RC; # хороший;

1.4.20. Интервал дискретизации (слева) соответствует ширине спектра сигнала (справа):

* 1мс; 0.5 кГц;

*1c; 0.5 Гц;

*5 мс; 100Гц;

*2мкс; 250 кГц;

Тесты по теме 1.7. «Теорема Котельникова»

1.7.1. Непрерывный гармонический сигнал имеет вид u(t)=cos2π*10³t. Интервал дискретизации по теореме Котельникова и первые три отсчета, начиная с момента t=0 , соответственно, равны:

* 0.5 мс; 1; -1; 1; # 0.5 мс; 0; 1; 0;

# 1мс; 1; -1; 1; # 0.5 мс; 1; 0; 1; # 1 мс; 0; -1; 1;

1.7.2. Непрерывный гармонический сигнал имеет вид u(t)=cos2π*10⁴t. Максимальная частота в спектре этого сигнала и первые три отсчета, начиная с момента t=0 , соответственно, равны

* 10⁴ Гц ; 1; -1; 1; # 10 кГц ; 1; 0; 1; #10⁴ Гц ; 1; 1; 1;

# 10⁴ рад/с ; 1; -1; 1;

1.7.3. Ширине спектра функции (слева) соответствует интервал дискретизации (справа):

* 0.1 кГц; * 5 мс;

* 1 мГц; * 0.5 мкс;

* 5 Гц; * 0.1 с;

* 0.25 Гц; * 2с ;

1.7.4. Ширине спектра функции (слева) соответствует частота дискретизации (справа):

* 0.1 кГц; * 0.2 кГц ;

* 1 мГц; * 12.56*10⁶ рад/с ;

* 31,4 р/с ; * 10 Гц ;

* 0.25 Гц; * 3.14 рад/с ;

1.7.5. Ширине спектра функции, дискретизированной в соответствии с теоремой Котельникова (слева), соответствует полоса пропускания идеального ФНЧ (справа) :

* 0.1 кГц; * 0.1 кГц ;

* 1 мГц; * 6.28*10⁶ рад/с ;

* 31,4 р/с ; * 5 Гц ;

* 0.25 Гц; * 1.57 рад/с ;

1.7.6. Порядок следования символов в формуле, определяющей интервал дискретизации по теореме Котельникова:

* Т; * =; * 1; * /; *2F_в ; # 3; # ^; # +;

1.7.7. Порядок следования символов в формуле, определяющей интервал дискретизации по теореме Котельникова:

* Т; * =; * π; * /; *ω_в ; # 3; # ^; # +;

1.7.8. Порядок следования символов в формуле, определяющей частоту дискретизации по теореме Котельникова:

* ω_д; * =; * 4; * π ; *F_в ; # 2; # -; # +;

1.7.9. Порядок следования символов в разложении функции в ряд Котельникова:

* x(t); * =; * 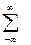; * x(kT) ; * ;

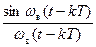# cos w _в(t-kT); # e^x ; # +;

1.7.10. Непрерывный гармонический сигнал имеет вид u(t)=0.5cos2π*10⁴t. Интервал дискретизации по теореме Котельникова и первые три отсчета, начиная с момента t=0 , соответственно, равны ____ мс, ___, ___, ___:

* 0.05 мс; 0.5; -0.5; 0.5;

1.7.11. Амплитудный спектр непрерывного сигнала имеет вид:

S(ω)= exp(-2ω/α); ω>0;

Частота дискретизации равна 2α. Относительная среднеквадратическая погрешность дискретизации данного сигнала в соответствии с теоремой Котельникова равна:

* е ^-4 ; # е ^–2; # α*е ^–2/3.14 ; # 0.5*е ^-3; # 0.5α*е ;

1.7.12. Порядок следования символов в формуле, определяющей среднеквадратическую погрешность дискретизации функции по теореме Котельникова:

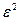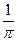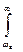* ; * ; * =; * ; *|S(w)|² ; *dw ; # S(w) ; # dt; # +;

1.7.13. На вход идеального ФНЧ подаются импульсы-отсчеты.

Порядок следования импульсов на выходе ИФНЧ:

* x(0) sinw_в t/ w_в t;

* x( T) sinw_в( t- T)/ w_в( t- T);

* x(2T) sinw _в (t-2T)/w_в (t-2T);

* x(3T) sinw _в (t-3T)/w_в (t-3T);

* x(4T) sinw _в (t-4T)/w_в (t-4T);

1.7.14. На вход RC фильтра нижних частот подаются импульсы-

отсчеты. Порядок следования импульсов на выходе ФНЧ:

* x(0) exp (-t/RC);

* x(T) exp [-(t-T)/RC];

* x(2T) exp [-(t-2T)/RC];

* x(3T) exp [-(t-3T)/RC];

* x(4 T) exp [-( t-4 T)/ RC];

1.7.15. Амплитудный спектр непрерывного сигнала имеет вид:

S(ω)= exp(-ω/α); ω<100рад/с;

Погрешность дискретизации данного сигнала в соответствии с теоремой Котельникова равна нулю, если частота дискретизации:

* больше или равна 200 рад/с; # равна 100рад/с ; # бесконечно мала; # равна 50 рад/с ;

1.7.16. Амплитудный спектр непрерывного сигнала имеет вид:

S(ω)= exp(-ω/α); ω>0;

* бесконечно велика; # равна α ; # бесконечно мала; # равна 2α ;

1.7.17. Амплитудный спектр непрерывного сигнала имеет вид:

S(ω)= exp(-ω/α); ω<50 рад/с;

* больше или равна 100 рад/с; # больше 50 рад/с ;

# бесконечно велика; # равна 50 рад/с ;

1.7.18. Теорема Котельникова справедлива точно для сигнала:

*с финитным спектром;

# с бесконечным спектром;

# с дискретным спектром;

# с неограниченным спектром;

1.7.19. Частота дискретизации равна:

* удвоенной ширине спектра сигнала;

# ширине спектра сигнала;

# половине ширины спектра сигнала;

# интервалу дискретизации;

1.7.20. Частота дискретизации по теореме Котельникова равна 1 кГц. Ширина спектра сигнала равна:

* 0.5 кГц; # 1 кГц; # 2 кГц; # 1 мс;

1.7.21. Частота дискретизации по теореме Котельникова

равна 6280 р/с. Ширина спектра сигнала равна:

* 0.5 кГц; # 1 кГц; # 2 кГц; # 1 мс;

1.7.22. Интервал дискретизации по теореме Котельникова равен 1 мс. Ширина спектра сигнала равна :

* 0.5 кГц; # 1 кГц; # 2 кГц; # 1 мс;

1.7.23. Интервал дискретизации по теореме Котельникова равен 0.5 мс. Ширина спектра сигнала равна :

* 6280рад/с ; # 6280 кГц; # 2 кГц; # 1 мс;

1.7.24. Сигнал описывается функцией времени u(t)=cos2πt . Соответствие отсчетов (справа) моментам времени (слева):

* 0 ; * 1 ;

* 0.5 ; * -1;

*1; * 1;

* 3; * 1;

# 0 ;

# 0;

1.7.25. Сигнал описывается функцией времени u(t)=2cos2πt . Отсчеты берутся в моменты времени t=0.5k ; k=0,1,2,3,4. Порядок следования отсчетов:

* 2 ; *-2 ; * 2 ; * -2; * 2;

Тесты по теме 1.5. «Случайные процессы и их характеристики»

1.5.1. Процесс называется детерминированным, если:

* его можно предсказать абсолютно точно;

# его значения предсказать абсолютно точно невозможно;

# он неизвестен получателю;

# его параметры неизвестны;

1.5.2. Процесс называется случайным, если:

* его значения предсказать абсолютно точно невозможно;

# его можно предсказать абсолютно точно;

# он гармонический;

# это единичный импульс;

1.5.3. Среднее значение случайного процесса обозначается следующим образом:

* m₁; # M₂; # m₂; # σ²;

1.5.4. Дисперсия случайного процесса обозначается следующим образом:

* M₂; * σ²; # m₁; # m₂;

1.5.5. Дисперсия случайного процесса - это:

* средняя мощность переменной составляющей случайного процесса;

# постоянная составляющая случайного процесса;

# переменная составляющая случайного процесса;

# мощность постоянной составляющей случайного процесса;

1.5.6. Нормальная функция плотности вероятности дана выражением:

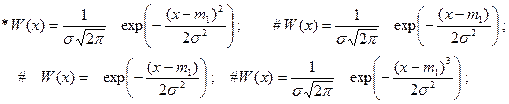
1.5.7. Дисперсия случайного процесса - это средняя _____________ переменной составляющей случайного процесса :

* мощность ; # амплитуда; # фаза; # частота;

1.5.8. Среднее значение случайного процесса - это _____________ составляющая случайного процесса :

* постоянная ; # мощность ; # амплитудная; # переменная; # частотная;

1.5.9. Второй начальный момент распределения - это полная средняя _____________ случайного процесса :

* мощность ; # амплитуда; # фаза; # частота; # дисперсия;

1.5.10. Площадь, ограниченная графиком W(x) и осью х, равна _____:

* 1 ; # 0; # 2; # -1; # ¥;

1.5.11. Одномерная ФРВ характеризует вероятность того, что случайный процесс принимает значения :

* x < x₀; # x = x₀; # x > x₀; # x < ¥; # x > ¥;

1.5.12. Нормальная функция плотности вероятности, имеющая среднее значение 2 и дисперсию 1 дана выражением:

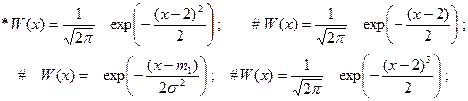
1.5.13. Порядок следования символов в формуле связывающей, числовые характеристики случайного процесса:

*σ² ; * =; * m₂; * - ; * m₁² ; # m₂² ; # m₁ ; # σ ;

1.5.14. Соответствие среднего значения и дисперсии (справа) нормальной ФПВ (слева):

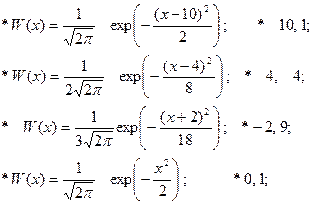
1.5.15. Соответствие нормальной ФПВ (справа) среднему значению и дисперсии (слева):

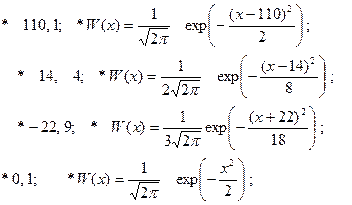
1.5.16. Соответствие значения аргумента (справа) значению нормальной ФРВ (слева):

* F(.) = 0 ; * - ∞ ;

* F(.)=0.5 ; * 0 ;

* F(.) = 1 ; * ∞;

1.5.17. Вероятность того, что нормальный случайный процесс, имеющий ФПВ вида :

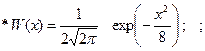
принимает значения больше 0, равна:

* 0.5; # 1; # 0; # ¥; # - ¥;

1.5.18. Вероятность того, что нормальный случайный процесс, имеющий ФПВ вида :

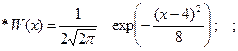
принимает значения больше ¥ , равна :

* 0; # 1; # 0.5; # ¥; # - ¥;

1.5.19. Порядок следования символов в формуле гауссовского распределения :

* W(x); * =; * 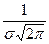; *exp; *[; *- ;

* ; * ] ;

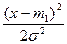1.5.20. Порядок следования символов в формуле релеевского распределения :

* W(x); * =; * 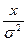; *exp; *(; *- ;

* ; * ) ;

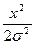1.5.21. Порядок следования символов в формуле равномерного распределения :

* W(x); * =; * 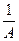; *при; *|x|; * < ;

* A/2 ;

1.5.22. Порядок следования символов в формуле, выражающей условие нормировки :

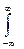* ; * W(x); * dx ; * =; * 1;

1.5.23. Порядок следования символов в формуле, определяющей среднее значение:

* m₁ ; * =; * 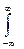; * x; * W(x); * dx ;

1.5.24. Порядок следования символов в формуле, определяющей второй начальный момент:

* m₂ ; * =; * 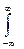; * x² ; * W(x); * dx ;

1.5.25. Порядок следования символов в формуле, определяющей дисперсию:

* σ² ; * =; * 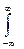; * (x - m₁)² ; * W(x); * dx ;

1.5.26. Вероятность того, что нормальный случайный процесс, имеющий ФПВ вида :

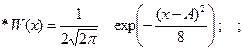
принимает значения больше А, равна:

* 0.5; # 1; # 0; # ¥; # - ¥;

1.5.27. Вероятность того, что нормальный случайный процесс, имеющий ФПВ вида :

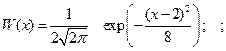
принимает значения меньше 2, равна:

* 0.5; # 1; # 0; # ¥; # - ¥;

1.5.28. Вероятность того, что нормальный случайный процесс, имеющий ФПВ вида :

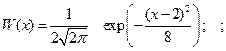
принимает значения больше 2, равна:

* 0.5; # 1; # 0; # ¥; # - ¥;

1.5.29. Вероятность того, что случайный процесс, имеющий ФПВ вида:

W(x)=1/4; при |x|<2

принимает значения меньше -1, равна :

* 0.25; # 0.5; # 1; # 0; # -1;

1.5.30. Порядок следования символов в формуле, определяющей вероятность того, что х >A:

* p(x>A); * =; * 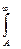; * W(x); * dx ; # 1; # x;

1.5.31. Порядок следования символов в формуле, выражающей связь ФРВ и ФПВ:

* F(x) ; * =; * 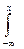; * W(x); * dx ; # d/dx; # x;

1.5.32. Порядок следования символов в формуле, выражающей связь ФПВ и ФРВ:

* W(x); * =; * 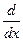; * F(x) ; # 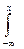; ; # x;

1.5.33. ФРВ случайного процесса равна:

F(x)=ax; при 0 < х < 0.5;

ФПВ имеет вид:

* W(x)=2; при 0<х<0.5; # W(x)=1; при 0<х<0.5;

# W(x)=1; при 0<х<1; # * W(x)=4; при 0<х<0.5;

1.5.34. ФПВ случайного процесса равна:

W(x)=а; при 0<х<0.25; W(x)=0; при х <0; x>0.25;

ФРВ имеет вид:

* F(x)=4x; при 0 < х < 0.25; # F(x)=4x; при 0 < х < 0.5;

# F(x)=2x; при 0 < х < 0.5; # F(x)=x; при 0 < х < 1;

1.5.35. Вероятность того, что нормальный случайный процесс, имеющий ФПВ вида :

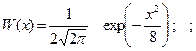
принимает значения от - ∞ до 0, равна:

* 0.5; # 1; # 0; # ¥; # - ¥;

1.5.36. Функция плотности вероятности случайного процесса

имеет вид:

W(x)= h; при |x| <2;

W(x)= 0; при |x| >2;

Параметр h равен :

*0.25; # 0.5; # 1; # 0; # -1;

1.5.37. Функция плотности вероятности случайного процесса

имеет вид:

W(x)= h; при |x| <5;

W(x)= 0; при |x| >5;

Параметр h равен :

*0.1; # 5; # 0.5; # 10; # 1;

1.5.38. Дана нормальная функция плотности вероятности:

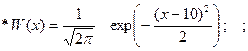
Среднее значение процесса равно :

*10; # 0.5; # 1; # 0; # -10;

1.5.39. Дана нормальная функция плотности вероятности:

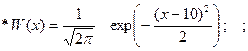
Дисперсия процесса равна:

*1; # 2; # 10; # 0; # -10;

1.5.40. Функция плотности вероятности случайного процесса

имеет вид:

W(x)= h; при |x| <2;

W(x)= 0; при |x| >2;

Среднее значение процесса равно:

*0; # 0.5; # 1; # 2; # h;

1.5.41. Среднее значение случайного процесса определяется выражением:

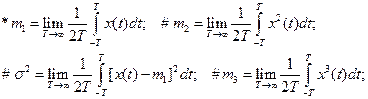
1.5.42. Дисперсия случайного процесса определяется выражением:

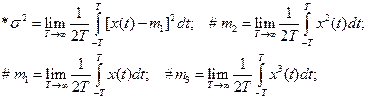
1.5.43. Соответствие названия символу:

* M₂; * дисперсия;

* m₁; * среднее значение;

* m₂ ; * второй начальный момент ;

# коэффициент гармоник;

# коэффициент усиления;

1.5.44. Полная средняя мощность случайного процесса определяется выражением:

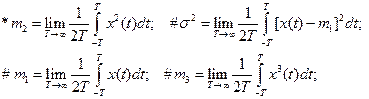
Тесты по теме 1.6. « Корреляционная функция»

1.6.1. Корреляционная функция обозначается следующим образом:

* B(t₁ ,t₂ ); * B(t₁-t₂ ); * B(τ); # B(ω);

1.6.2. Корреляционная функция характеризует:

* степень статистической связи двух значений случайного процесса;

# среднее значение процесса;

# амплитуду процесса;

1.6.3. Энергетический спектр случайного процесса - это:

* зависимость энергии составляющих процесса от частоты;

# зависимость энергии составляющих процесса от времени;

# зависимость фазы составляющих процесса от частоты;

# зависимость амплитуды составляющих процесса от частоты;

1.6.4. Корреляционная функция и энергетический спектр случайного процесса связаны преобразованием:

* Винера-Хинчина ; # Фурье; # Лопиталя; # Тейлора;

1.6.5. Ширина энергетического спектра и интервал корреляции случайного процесса:

* обратно пропорциональны друг другу;

# прямо пропорциональны друг другу;

# независимы;

1.6.6. Спектральная плотность белого шума на единичном сопротивлении равна 2 вт/Гц. Дисперсия белого шума в полосе частот 628р/с равна:

*200 вт; # 100 вт; # 628 вт ; # 1256 вт; # 2 вт ;

1.6.7. Соответствие мощности белого шума в полосе частот 628р/с (справа) спектральной плотности белого шума на единичном сопротивлении (слева):

*3 вт/Гц; *300вт.;

*15 вт/Гц; * 1500 вт;

*0,11 вт/Гц; * 11 вт;

1.6.8. Дисперсия белого шума в полосе частот 628р/с равна 1000 вт. Спектральная плотность белого шума на единичном сопротивлении равна ______ вт/Гц:

*10;

1.6.9. Спектральная плотность белого шума – это мощность шума, приходящаяся на полосу частот:

* 1 Гц; # 1 вт ; # 1 с; # 1 мс ;

1.6.10. Спектральная плотность белого шума на единичном сопротивлении равна 2 вт/Гц. Полоса частот, в которой дисперсия белого шума равна 1000 вт, составляет :

*3140 рад/с; # 100 Гц ; #3140 Гц ; # 1000 Гц ;

1.6.11. Корреляционная функция случайного процесса равна:

B(τ)=5*ехр(-4 τ)

Дисперсия процесса на единичном сопротивлении равна :

*5 вт; # 4 вт; # 1 вт; # 0 вт; # 20 вт;

1.6.12. Корреляционная функция случайного процесса равна:

B(τ)=16*ехр(-2 τ)

Средняя мощность процесса на единичном сопротивлении равна:

*16; # 2 вт; # 1 вт; # 0 вт; # 32 вт;

1.6.13. Корреляционная функция случайного процесса при τ=0 - это

__________ процесса :

* дисперсия; * средняя мощность переменной составляющей;

1.6.14. Интервал корреляции случайного процесса __________ пропорционален ширине энергетического спектра:

* обратно; # прямо;

1.6.15. Энергетический спектр случайного процесса – это зависимость энергии составляющих процесса от:

* частоты; # времени; # фазы; # амплитуды; # напряжения;

1.6.16. Интервал корреляции можно определить как интервал времени, в течение которого корреляционная функция:

B(τ)=24*sin 6.28τ/6.28τ;

изменяется от максимального значения до 0. Интервал корреляции для

данной функции B(τ) равен:

* 0.5 с ; # 1 с ; # 0 ; # 0.1 с ; # 2 с ;

1.6.17. Интервал корреляции можно определить как интервал времени, в течение которого корреляционная функция:

B(τ)=4*sin 628τ/628τ;

изменяется от максимального значения до 0. Интервал корреляции для

данной функции B(τ) равен :

* 0.005 с ; # 0.5 с ; # 0 ; # 0.05 с ; # 1 с ;

1.6.18. Интервал корреляции уменьшился в 3 раза. Следовательно, ширина энергетического спектра этого процесса :

* увеличилась в 3 раза; # уменьшилась в 3 раза;

# увеличилась в 9 раз ; # уменьшилась в 9 раз ;

1.6.19. Интервал корреляции уменьшился в 4 раза. Следовательно, ширина энергетического спектра этого процесса :

* увеличилась в 4 раза; # уменьшилась в 4 раза;

# увеличилась в 16 раз ; # уменьшилась в 16 раз ;

1.6.20. Интервал корреляции увеличился в 2 раза. Следовательно, ширина энергетического спектра этого процесса :

* уменьшилась в 2 раза ; # увеличилась в 2 раза;

# увеличилась в 4 раза ; # уменьшилась в 4 раза;

1.6.21. Постоянная составляющая процесса х равна 2. Процесс y=2x. Среднее значение процесса y равно:

* 4 ; # 2; # 0 ; # 1 ;

1.6.22. Среднее значение процесса х равно 1. Процесс y=2x -1. Постоянная составляющая процесса y равна ____.

* 1 ; # 2; # 0 ; # 1 ;

1.6.23. Дисперсия процесса х равна 2, а среднее значение равно 0. Процесс y=2x. Дисперсия процесса y равна :

* 8 ; # 2; # 0 ; # 1 ;

1.6.24. Средняя мощность переменной составляющей процесса х равна 3, а среднее значение равно 0. Процесс y=2x. Дисперсия процесса y равна:

* 12 ; # 6; # 0 ; # 18 ;

1.6.25. На входе линейной цепи действует нормальный случайный процесс. Процесс на выходе этой цепи :

* нормальный ; # не нормальный; # детерминированный ;

# равен 0 ;

1.6.26. Нормальный случайный процесс, имеющий ФПВ вида :

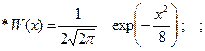
подвергается нелинейному преобразованию y=x² . ФПВ процесса y имеет вид:

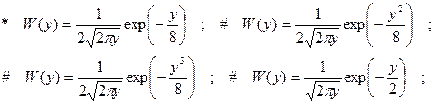
1.6.27. Нормальный случайный процесс, имеющий ФПВ вида :

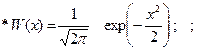
подвергается нелинейному преобразованию y=|x| . ФПВ процесса y имеет вид:

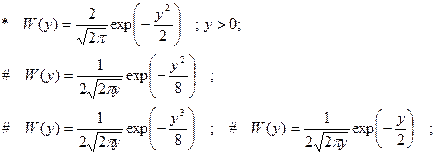
1.6.28. Нормальный случайный процесс, имеющий ФПВ вида :

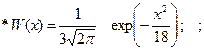
подвергается преобразованию y=x +1 . ФПВ процесса y имеет вид:

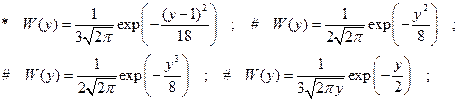
1.6.29. Нормальный случайный процесс, имеющий ФПВ вида :

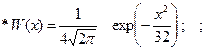
подвергается преобразованию y=2x . ФПВ процесса y имеет вид:

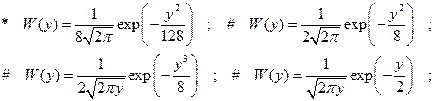
1.6.30. Нормальный случайный процесс, имеющий ФПВ вида :

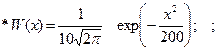
подвергается преобразованию y=2x+2 . ФПВ процесса y имеет вид:

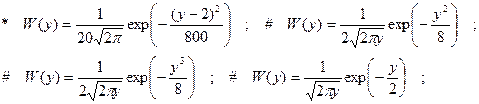
Тесты по теме 2.1: Аппроксимация характеристик.

Тесты по теме 2.2: Метод кратных дуг.

Тесты по теме 2.3: Метод угла отсечки.

Тесты по теме 2.4: Метод трех и пяти ординат

Тесты по теме 2.5: Бигармоническое воздействие

2.1.1. Заданную таблично или графически, нелинейную характеристику можно представить аналитически посредством:

* аппроксимации; # дискретизации; # ортогонализации; # модуляции.

2.1.2. ВАХ аппроксимирована соотношением: 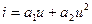. Ток измеряется в амперах (А), напряжение в вольтах (В). Размерность коэффициента a₁:

* А/В # А # А²/В² # А²/В

2.1.3. Аппроксимация, при которой нелинейная характеристика представляется степенным рядом:

* полиномиальная; # трансцендентная; # кусочно-линейная; # экспоненциальная

2.1.4. Аппроксимация, при которой нелинейная характеристика представляется отрезками прямых:

* кусочно-линейная; # полиномиальная; # трансцендентная; # кусочно-постоянная;

2.1.5. Точность полиномиальной аппроксимации при увеличении степени полинома:

* увеличивается; # уменьшается; # не изменяется; # равна нулю

2.1.6. ВАХ аппроксимирована соотношением: 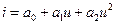. Ток измеряется в амперах (А), напряжение в вольтах (В). Размерность коэффициента a₀

* А # А² # А²/В² # А²/В

2.1.7. ВАХ аппроксимирована соотношением: 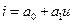, и определена двумя координатами (u₁; i₁)=(0; 0); (u₂; i₂)=(2; 2). Коэффициенты полинома равны

* 0; 1 # 0; 1,5 # 2; 2 # 0; 0 # 1; 1.

2.1.8. Вольт-амперная характеристика (ВАХ) задана в виде: 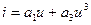, и определена двумя координатами (u₁; i₁)=(1; 2,5); (u₂; i₂)=(2; 2). Коэффициенты полинома равны

* 3; -0,5 # -2; 1,5 # 2,5; 3 # 0,5; 3 # 2; -0,5

2.1.9. ВАХ аппроксимирована соотношением: 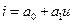, и определена двумя координатами (u₁; i₁)=(0; 1); (u₂; i₂)=(2; 2). Коэффициенты полинома равны

* 1; 0.5 # 0; 1,5 # 0; 1 # 2;3 # 1; 1.

2.1.10. Аппроксимация двумя отрезками прямых преимущественно применяется для анализа работы нелинейной цепи (НЦ) в режиме ____ амплитуд

* больших; # малых; # любых

2.1.11. Степенная аппроксимация преимущественно применяется для анализа работы нелинейной цепи (НЦ) в режиме ____ амплитуд

* малых; # больших; # любых

2.1.12. ВАХ аппроксимирована соотношением: i=0, u<U₀; i=2+u, u> U₀. Напряжение отсечки U₀ и крутизна линейного участка S равны

* -2; 1 # 2; 1 # 1; -1 # 2; 2

2.1.13. ВАХ аппроксимирована соотношением: 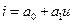, и определена двумя координатами (u₁; i₁)=(0; 2); (u₂; i₂)=(2; 2). Коэффициенты полинома равны

* 2; 0 # 0; 1,5 # 0; 1 # 0; 0 # 2; 2.

2.1.14 ВАХ аппроксимирована соотношением: 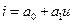, и определена двумя координатами (u₁; i₁)=(0; 3); (u₂; i₂)=(2; 6). Коэффициенты полинома равны

* 3; 1.5 # 0; 1,5 # 3; 3 # 0; 0 # 1; 3.

2.1.15 ВАХ аппроксимирована соотношением: 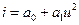, и определена двумя координатами (u₁; i₁)=(0; 3); (u₂; i₂)=(1; 6). Коэффициенты полинома равны

* 3; 3 # 0; 1,5 # 1; 3 # 2; 1 # 1; 1.

2.2.1. При полиномиальной аппроксимации характеристики нелинейной безынерционной цепи применим спектральный анализ по методу:

* кратных дуг; # угла отсечки; # трех ординат; # пяти ординат

2.2.2. На нелинейную цепь, ВАХ которой аппроксимирована полиномом: 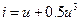, воздействует гармоническое колебание 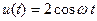. Амплитуда первой гармоники отклика равна:

* 5; # 3; # 2; # 4

2.2.3. На нелинейную цепь, ВАХ которой аппроксимирована полиномом: 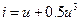, воздействует гармоническое колебание 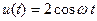. Амплитуда третьей гармоники отклика равна:

* 1; # 3; # 2; # 4

2.2.4. Отклик нелинейной безынерционной цепи на гармоническое воздействие содержит составляющие на частотах _____ частоте воздействия:

* кратных; # не кратных; # комбинированных; # относительных

2.2.5. На нелинейную цепь, ВАХ которой аппроксимирована полиномом: 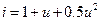, воздействует гармоническое колебание 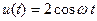. Амплитуда второй гармоники отклика равна:

* 1; # 3; # 2; # 4

2.2.6. На нелинейную цепь, ВАХ которой аппроксимирована полиномом: 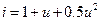, воздействует гармоническое колебание 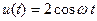. Амплитуда постоянной составляющей отклика равна:

* 2; # 3; # 1; # 4

2.2.7. На нелинейную цепь, ВАХ которой аппроксимирована полиномом: 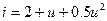, воздействует гармоническое колебание 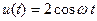. Амплитуда постоянной составляющей отклика равна:

* 3; # 1; # 2; # 4

2.2.8. На нелинейную цепь, ВАХ которой аппроксимирована полиномом: 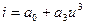, воздействует гармоническое колебание. Спектр отклика содержит составляющих всего:

* три; # две; # одну; # четыре

2.2.9. На нелинейную цепь, ВАХ которой аппроксимирована полиномом: 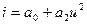, воздействует гармоническое колебание. Амплитуда первой гармоники отклика равна:

* 0; # 1; # 2; # 1/2

2.2.10. На нелинейную цепь, ВАХ которой аппроксимирована полиномом: 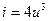, воздействует гармоническое колебание. Амплитуда второй гармоники отклика равна:

* 0; # 3; # 2; # 1

2.2.11. На нелинейную цепь, ВАХ которой аппроксимирована полиномом: 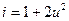, воздействует гармоническое колебание 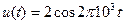. Постоянная составляющая отклика равна:

* 5; # 1; # 0; # 3

2.2.12. На нелинейную цепь, ВАХ которой аппроксимирована полиномом: 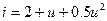, воздействует гармоническое колебание 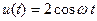. Амплитуда второй гармоники отклика равна:

* 1; # 3; # 2; # 4

2.2.13. На нелинейную цепь, ВАХ которой аппроксимирована полиномом: 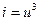, воздействует гармоническое колебание 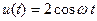. Амплитуда первой гармоники отклика равна:

* 6; # 3; # 2; # 1

2.2.14. На нелинейную цепь, ВАХ которой аппроксимирована полиномом: 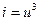, воздействует гармоническое колебание 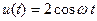. Амплитуда третьей гармоники отклика равна:

* 2; # 3; # 6; # 1

2.2.15. На нелинейную цепь, ВАХ которой аппроксимирована полиномом: 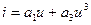, воздействует гармоническое колебание. Частота входного колебания 2 кГц. Спектр выходного тока содержит частоты:

* 2 кГц и 6 кГц; # 0 кГц и 2 кГц; # 2 кГц и 4 кГц; # 1 кГц и 3 кГц;

2.2.16. На нелинейную цепь, ВАХ которой аппроксимирована полиномом: 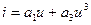, воздействует гармоническое колебание. Частота входного колебания 5 кГц. Спектр выходного тока содержит частоты:

* 5 кГц и 15 кГц; # 0 кГц и 5 кГц; # 5 кГц и 10 кГц; # 1 кГц и 3 кГц;

2.2.17. На нелинейную цепь, ВАХ которой аппроксимирована полиномом: 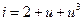, воздействует гармоническое колебание 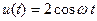. Амплитуда постоянной составляющей отклика равна:

* 2; # 1; # 3; # 4

2.2.18. На нелинейную цепь, ВАХ которой аппроксимирована полиномом: 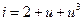, воздействует гармоническое колебание 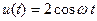. Амплитуда первой гармоники отклика равна:

* 8; # 2; # 6; # 4

2.2.18. На нелинейную цепь, ВАХ которой аппроксимирована полиномом: 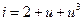, воздействует гармоническое колебание 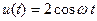. Амплитуда третьей гармоники отклика равна:

* 2; # 6; # 8; # 4

2.2.19. На нелинейную цепь, ВАХ которой аппроксимирована полиномом: 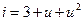, воздействует гармоническое колебание 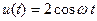. Амплитуда постоянной составляющей отклика равна:

* 5; # 2; # 1; # 4

2.2.20. На нелинейную цепь, ВАХ которой аппроксимирована полиномом: 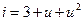, воздействует гармоническое колебание 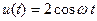. Амплитуда второй гармоники отклика равна:

* 2; # 5; # 1; # 4

2.3.1. При аппроксимации характеристики нелинейной безынерционной цепи двумя отрезками прямых применим спектральный анализ по методу:

* угла отсечки; # кратных дуг; # трех ординат; # пяти ординат

2.3.2. На входе нелинейной цепи действует напряжение: 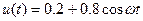(В). Напряжение отсечки 0.6 (В). Угол отсечки равен:

* 60⁰; # 50⁰; # 30⁰; # 80⁰

2.3.3. Крутизна линейного участка ВАХ 25 мА/В. Значение коэффициента Берга 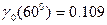. Входное напряжение: 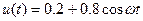(В). Постоянная составляющая тока отклика:

* 2.18 мА; # 1.09 мА; # 2 мА; # 2.4 мА

2.3.4. Крутизна линейного участка ВАХ 25 мА/В. Значение функции Берга 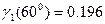. Входное напряжение: 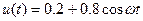(В). Амплитуда первой гармоники тока отклика:

* 3.92 мА; # 2.09 мА; # 2.5 мА; # 4 мА

2.3.5. На входе нелинейной цепи действует напряжение: 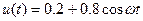(В). Напряжение отсечки Е₀= - 0.6 (В). Угол отсечки равен:

* 180⁰; # 50⁰; # 30⁰; # 80⁰

2.3.6. На входе нелинейной цепи действует напряжение: 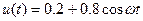(В). Напряжение отсечки 0.2 (В). Угол отсечки равен:

* 90⁰; # 50⁰; # 30⁰; # 80⁰

2.3.7. При поддержании постоянным максимального значения тока отклика цепи с кусочно-линейной ВАХ, амплитуда 2-ой гармоники отклика максимальна при угле отсечки

* 60⁰; # 180⁰; # 90⁰; # 150⁰

2.3.8. При поддержании постоянным максимального значения тока отклика цепи с кусочно-линейной ВАХ, амплитуда 3-ой гармоники отклика максимальна при угле отсечки

* 40⁰; # 60⁰; # 90⁰; # 50⁰

2.3.9. При поддержании постоянным максимального значения тока отклика цепи с кусочно-линейной ВАХ, амплитуда 4-ой гармоники отклика максимальна при угле отсечки

* 30⁰; # 45⁰; # 90⁰; # 60⁰

2.3.10. При постоянной амплитуде гармонического воздействия на цепь с кусочно-линейной ВАХ, амплитуда 2-ой гармоники отклика максимальна при угле отсечки

* 90⁰; # 40⁰; # 80⁰; # 60⁰

2.3.11. При постоянной амплитуде гармонического воздействия на цепь с кусочно-линейной ВАХ, амплитуда 3-ой гармоники отклика максимальна при угле отсечки

* 60⁰; # 40⁰; # 80⁰; # 90⁰

2.3.12. При постоянной амплитуде гармонического воздействия на цепь с кусочно-линейной ВАХ, амплитуда 4-ой гармоники отклика максимальна при угле отсечки

* 45⁰; # 30⁰; # 90⁰; # 60⁰

2.3.13. На выходе нелинейного элемента ток протекает в течение 1/2 части периода. Угол отсечки равен:

* 90⁰; # 45⁰; # 30⁰; #60⁰

2.3.14. На выходе нелинейного элемента ток протекает в течение 1/8 части периода. Угол отсечки равен:

* 22,5⁰; # 45⁰; # 30⁰; #60⁰

2.3.15. На выходе нелинейного элемента ток протекает в течение 1/6 части периода. Угол отсечки равен:

* 30⁰; # 90⁰; # 45⁰; #60⁰

2.3.16. На выходе нелинейного элемента ток протекает в течение ¼ части периода. Угол отсечки равен:

* 45⁰; # 90⁰; # 30⁰; #60⁰

2.3.17. Напряжение смещения равно напряжению отсечки. При увеличении амплитуды гармонического воздействия на цепь с кусочно-линейной ВАХ, угол отсечки равен:

* 90⁰; # 0⁰; # 60⁰; # 180⁰

2.3.18. Оптимальный угол отсечки для n-ой гармоники отклика цепи при постоянной амплитуде гармонического воздействия :

* 180/n; # 120/n; # 90/n; # 150/n

2.3.19. Соответствие буквы и её наименования в формуле входного сигнала нелинейной цепи: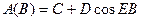

* мгновенное напряжение - A; * время - B; * напряжение смещения - C; * амплитуда сигнала - D; * частота - E

2.3.20. Соответствие буквы и её наименования в формуле метода угла отсечки: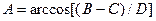

* угол отсечки - A; * напряжение отсечки - B; * напряжение смещения – C; * амплитуда сигнала - D;

2.3.21. Оптимальный угол отсечки для n-ой гармоники отклика цепи при поддержании постоянным максимального значения тока отклика :

* 120/n; # 180/n; # 90/n; # 150/n

2.3.22. Напряжение смещения – E, напряжение отсечки - Е₀, амплитуда гармонического воздействия на НБЦ с кусочно-линейной ВАХ – U_m. Косинус угла отсечки равен:

* (Е-Е₀)/U_m ; #(Е- U_m)/ Е₀; # (U_m -Е₀)/ Е; # (Е-Е₀).

2.4.1. Амплитуды спектра тока отклика НБЦ при использовании метода трех ординат

* (I₀, I₁, I₂); # (I₁, I₂, I₃); # (I₀, I₂, I₄); # (I₁, I₃, I₅)

2.4.2. Амплитуды спектра тока отклика НБЦ при использовании метода пяти ординат

* (I₀, I₁, I₂, I₃, I₄); # (I₁, I₂, I₃, I₄, I₅); # (I₀, I₂, I₄, I₆, I₈); # (I₁, I₃, I₅, I₇, I₉)

2.4.3. Количество гармонических составляющих в спектре тока отклика нелинейной цепи при использовании метода трех ординат

* 2; # 0; # 1; # 3

2.4.4. Количество гармонических составляющих в спектре тока отклика нелинейной цепи при использовании метода пяти ординат

* 4; # 2; # 5; # 3

2.4.5. При использовании метода трех ординат получены значения токов ВАХ: i_min=4 мА, i₀=10 мА, i_max=20 мА. Амплитуда первой гармоники тока

* 8 мА; # 1 мА; # 11 мА; # 4 мА

1 / 5 1 2 3 4 5

Следующая > >>