Динамика вращательного движения

Дата: 2025-06-02; Просмотры: 7
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

9. Основной закон динамики вращательного движения материальной точки. Момент инерции. Теорема Штейнера.
Основной закон динамики вращательного движения материальной точки: угловое ускорение пропорционально моменту внешних сил, обратно пропорционально моменту инерции и направлено в сторону равнодействующего момента сил.
Момент инерции – физическая величина, равная сумме произведений элементарных масс на квадраты их расстояний до рассматриваемой оси. .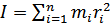
Теорема Штейнера: момент инерции тела I относительно произвольной оси вращения равен моменту его инерции 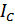относительно параллельной оси, проходящей через центр масс тела, сложенному с произведением массы m тела на квадрат расстояния a между ними: .

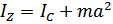10. Кинетическая энергия вращающегося тела.

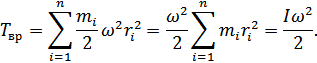
11. Момент импульса и закон его сохранения.
Момент импульса – физическая величина, определяемая векторным произведением радиуса вектора 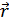материальной точки, проведённого из точки O, на импульс 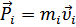этой материальной точки: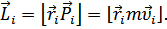
Закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т.е. не изменяется с течением времени при любых взаимодействиях тел этой системы.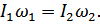

Элементы специальной теории относительности

12. Механический принцип относительности. Классический закон сложения скоростей; Ускорение и длина отрезка в различных инерциальных системах отсчёта.
Механический принцип относительности: во всех ИСО механические процессы протекают одинаково.
Классический закон сложения скоростей: скорость тела, одновременно участвующего в двух движениях, равна векторной сумме скоростей этого движения.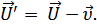
Ускорение в различных ИСО: ускорение в разных ИСО в классической механике является неизменной величиной. Величины, которые не меняются при переходе от одной СО к другой, называются инвариантными.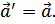
Длина отрезка в различных ИСО: в различных ИСО длина отрезка одинакова.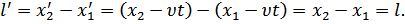

13. Постулаты специальной теории относительности.
1) Принцип относительности: никакие опыты, проведённые внутри данной ИСО, не дают возможность обнаружить, покоится ли эта СО или движется равномерно и прямолинейно; все законы природы инвариантны, по отношению к переходу от одной ИСО к другой, т.е. все ИСО равноправны: во всех таких системах все явления природы протекают одинаково.
2) Принцип постоянства скорости света: скорость света в вакууме не зависит от скорости движения источника света или наблюдателя и одинакова во всех ИСО. Скорость света величина инвариантная, это максимально возможная скорость.

14. Преобразования Лоренца. Релятивистский эффект: длина тел в разных системах отсчёта (Лоренцево сокращение длины).
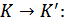
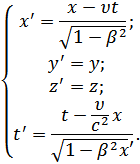При
При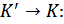
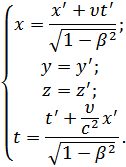Длина тел в разных СО: линейные размеры тела наибольшие в той ИСО, относительно которой тело покоится. Линейный размер тела, движущегося относительно ИСО, уменьшается в направлении движения в 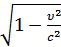раз, т.е. так называемое Лоренцево сокращение длины тем больше, чем больше скорость движения.

15. Преобразования Лоренца. Релятивистский эффект: длительность событий в разных системах отсчёта.
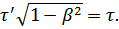 Длительность событий в разных СО: длительность события, происходящего в некоторой точке, наименьшая в той ИСО, относительно которой эта точка неподвижна.

16. Релятивистский закон сложения скоростей.

 

Релятивистский закон сложения скоростей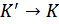
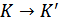
Общий случай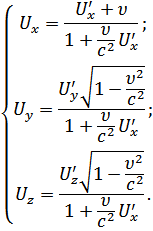
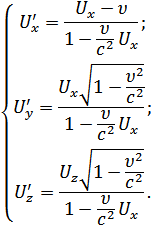
Частный случай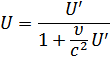

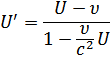
Элементы гидроаэромеханики

17. Давление в жидкости и газе. Законы Паскаля и Архимеда. Гидростатические давление.
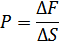Закон Паскаля: давление в любом месте жидкости (газа) одинаков по всем направлениям, причём давление одинаково передаётся по всему объёму.
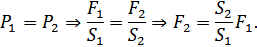Закон Архимеда: на тело, погружённое в жидкость (газ), действует со стороны этой жидкости направленная вверх выталкивающая сила, равная весу жидкости или газа, вытесненного телом.
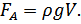Гидростатическое давление: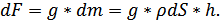

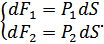
18. Установившееся движение жидкости. Уравнение неразрывности для несжимаемой жидкости.
Установившееся движение жидкости – течение жидкости, при котором форма и расположение линий тока, а также значения скоростей в каждой её точке со временем не меняются.
Уравнение неразрывности для несжимаемой жидкости: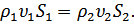

19. Уравнение Бернулли. Статическое и динамическое давление.
Уравнение Бернулли – выражение закона сохранения энергии применительно к установившемуся течению идеальной жидкости.
; .
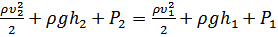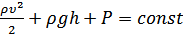Статическое давление – давление, которое оказывает жидкость на поверхность обтекаемого ею тела. P .
Динамическое давление – дополнительное давление, которое создаёт жидкость при её остановке. .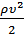

20. Вязкость. Сила внутреннего трения. Режимы течения жидкостей. Число Рейнольдса.
Вязкость – свойство реальных жидкостей оказывать сопротивление перемещению одной части жидкости относительно другой.
Сила внутреннего трения - 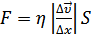тем больше, чем больше площадь поверхности слоя S , и зависит от того, насколько быстро меняется скорость течения жидкости при переходе от слоя к слою.
Ламинарное (слоистое) течение – течение, при котором каждый выделенный тонкий слой скользит относительно соседних, не перемешиваясь с ними.
Вихревое (турбулентное) течение – это течение, при котором вдоль потока происходит интенсивное вихреобразование и перемешивание жидкости (газа).
Число Рейнольдса: .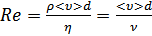

Основы молекулярной физики и термодинамики

21. Модель идеального газа. Опытные законы идеальных газов. Уравнение состояния идеального газа.
Модель идеального газа – модель, согласно которой собственный объём молекул газа пренебрежимо мал по сравнению с объёмом сосуда; между молекулами газа отсутствуют силы взаимодействия; столкновения молекул газа между собой и со стенками сосуда абсолютно упругие.
Закон Бойля-Мариотта для изотермического процесса ( T = const ):
PV=const при m = const и T = const.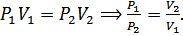
Закон Гей-Люссака для изобарного процесса ( P = const ):
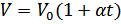 , при P = const ; m = const . .
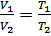Закон Гей-Люссака для изохорного процесса ( V = const ):
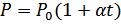 , при V = const ; m = const . .
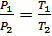Закон Авогадро. Моли любых газов при одинаковых температуре и давлении занимают одинаковые объёмы.
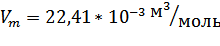, н.у. .
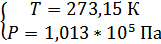Уравнение состояния идеального газа: .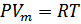

22. Основное уравнение молекулярно-кинетической теории идеальных газов.
 .

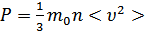23. Закон Максвелла о распределении по скоростям и энергиям теплового движения. Зависимость распределения Максвелла от температуры.
. .

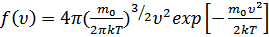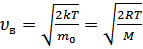24. Барометрическая формула. Распределение Больцмана.
Барометрическая формула: .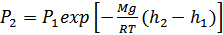
Распределение Больцмана: на каждую степень свободы (поступательную и вращательную) приходится в среднем одинаковая кинетическая энергия, равная 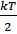, а на колебательную степень свободы – энергия, равная kT . Согласно закону распределения, среднее значение энергии одной молекулы 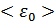тем больше, чем сложнее молекула, чем больше у неё степеней свободы.

25. Явления переноса в газах.
В газе возникают потоки энергии, вещества, а также импульса упорядоченного движения частиц. Эти потоки, характерные для неравновесных состояний газа, являются основой кинетических явлений, объединённых общим названием – явления переноса.

26. Реальные газы. Уравнение Ван-Дер-Ваальса.
Реальный газ – газ, который не описывается в точности уравнением Клапейрона-Менделеева.

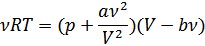
27. Внутренняя энергия термодинамической системы. Работа газа при его расширении.
Внутренняя энергия термодинамической системы U – энергия хаотического (теплового) движения микрочастиц системы (молекул, атомов, электронов, ядер) и энергия взаимодействия этих частиц.
.

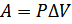28. Первое начало термодинамики и его применение к изопроцессам.
Первое начало термодинамики – закон сохранения и превращения энергии применительно к термодинамическим системам.

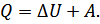
29. Теплоёмкость идеального газа. Уравнение Майера. Политропные процессы. Уравнение политропы.
Теплоёмкость идеального газа: .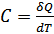
Уравнение Майера: .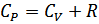
Политропные процессы – термодинамические процессы, во время которых теплоёмкость газов остаётся неизменной.
. .

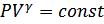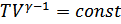30. Круговой процесс (цикл). Обратимые и необратимые процессы. Тепловой двигатель. Холодильная машина.
Круговой процесс – процесс, при котором система, пройдя через ряд состояний, возвращается в исходное состояние.
Обратимый процесс – процесс, способный протекать как в прямом, так и в обратном направлениях.
Необратимый процесс – всякий иной по отношению к обратимым процессам процесс.
Тепловой двигатель – это периодический действующий двигатель, совершающий работу за счёт получения извне теплоты. В тепловых двигателях используют прямой цикл.
Холодильная машина – периодический действующая машина, в которой за счёт работы внешних сил теплота переносится к телу с более высокой температурой.

31. Цикл Карно и работа за цикл. Теорема Карно.
Цикл Карно – наиболее экономичный обратимый круговой цикл, состояий из двух изотерм и двух адиабат. .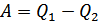
Согласно теореме Карно, для цикла Карно КПД действительно определяется только температурами нагревателя и холодильника.

32. Энтропия. Второе начало термодинамики.
Энтропия – это функция состояния, дифференциалом которой является приведённое количество теплоты .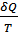
Второе начало термодинамики. Любой процесс в замкнутой системе происходит так, что энтропия системы при этом не убывает.

Электростатика и законы постоянного тока

1. Электрический заряд и его свойства. Закон сохранения электрического заряда. Взаимодействие зарядов. Закон Кулона.
Электрический заряд q – это физическая величина, которая характеризует свойство тел или частиц вступать в электромагнитные взаимодействия и определяет значения сил и энергий при таких взаимодействиях. Ему принадлежат следующие фундаментальные свойства:
1) электрический заряд существует в двух видах: отрицательные и положительные заряды;
2) электрический заряд дискретен;
3) алгебраическая сумма электрических зарядов замкнутой системы остаётся постоянной (закон сохранения электрического заряда);
4) электрический заряд – величина релятивистки инвариантная, т.е. не зависит от системы отсчёта, а значит, не зависит от того, движется заряд или покоится.
Закон сохранения электрического заряда: электрические заряды не возникают и не исчезают, они могут быть лишь переданы от одного тела другому или перемещены внутри данного тела.
Сила взаимодействия неподвижных точечных электрических зарядов подчиняется закону электростатического взаимодействия.
Закон Кулона: сила взаимодействия 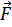между двумя неподвижными точечными зарядами, находящимися в вакууме, пропорциональна зарядам 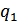и 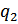и обратно пропорциональна квадрату расстояния r между ними.

2. Электростатическое поле. Напряжённость поля. Графическое изображение электростатических полей. Принцип суперпозиции.
Электростатическое поле – поле, созданное неподвижными электрическими зарядами.
Напряжённость поля – вектор 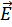, численно равный силе, с которой это поле действует на единичный положительный заряд, помещённый в данную точку и направленный в сторону действия силы.
Графическое изображение электростатических полей. Графически электростатическое поле изображают с помощью силовых линий или линий напряжённости.
Принцип суперпозиции электростатических полей: напряжённость 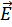результирующего поля системы точечных зарядов равна векторной сумме напряжённостей полей, создаваемых каждым из этих зарядов в отдельности.

3. Поток вектора напряжённости. Теорема Остроградского-Гаусса для электростатического поля в вакууме.
Поток вектора напряжённости – для однородного поля и плоской поверхности число линий напряжённости, пронизывающих площадку S, пропорционально величине площадки S и зависит от угла 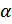между нормалью 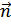к площадке с вектором .
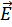Теорема Остроградского-Гаусса. Поток вектора напряжённости электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен заряду, заключённому в объёме, ограниченном этой поверхностью, и делённому на .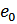

4. Работа перемещения заряда в электростатическом поле. Теорема о циркуляции вектора напряжённости электростатического поля. Потенциал электростатического поля. Разность потенциалов. Связь напряжённости и потенциала. Эквипотенциальные поверхности.
Работа перемещения заряда в электростатическом поле: .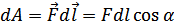
Теорема о циркуляции вектора 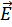: Циркуляция вектора напряжённости электростатического поля вдоль любого замкнутого контура равна нулю.
Потенциал электростатического поля – это скалярная физическая величина, определяемая потенциальной энергией единичного положительного заряда, помещённого в данную точку поля.
Разность потенциалов двух точек определяется в электростатическом поле определяется работой, совершаемой силами поля, при перемещении единичного положительного заряда из точки 1 в точку 2.
Связь напряжённости и потенциала: .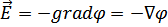
Эквипотенциальные поверхности. Для графического изображения распределения потенциала электростатического поля пользуются эквипотенциальными поверхностями.

5. Вещество в электрическом поле. Типы диэлектриков. Поляризация диэлектриков. Поляризованность, диэлектрическая восприимчивость вещества, относительная диэлектрическая проницаемость.
Внесение всех диэлектриков во внешнее электрическое поле приводит к возникновению у них отличного от нуля результирующего электрического дипольного момента, т.е. к поляризации диэлектрика.
Виды диэлектриков: диэлектрики с неполярными молекулами, диэлектрики с полярными молекулами, ионные диэлектрики.
Поляризация диэлектрика – процесс ориентации диполей или появления под воздействием внешнего электрического поля ориентированных по полю диполей.
Поляризованность 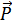– физическая величина, равная дипольному моменту единицы объёма диэлектрика.
Диэлектрическая восприимчивость – безразмерная положительная величина, характеризующая свойства диэлектрика.
Относительная диэлектрическая проницаемость среды связана с диэлектрической восприимчивостью соотношением.

6. Вектор электрического смещения. Поток вектора электрического смещения. Теорема Гаусса электростатического поля в диэлектрическом поле.
Вектор электрического смещения 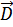описывает электростатическое поле, создаваемое свободными зарядами, но при таком их распределении в пространстве, какое имеется при наличии диэлектрика.
Поток вектора электрического смещения равен алгебраической сумме заключённых внутри этой поверхности сторонних электрических зарядов.
Теорема Остроградского-Гаусса для электростатического поля в диэлектрике. Поток вектора смещения электростатического поля в диэлектрике сквозь произвольную замкнутую поверхность равен свободному заряду, заключённому в объёме, ограниченном этой поверхностью.

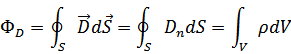
7. Проводники в электростатическом поле. Типы проводников. Напряжённость поля внутри проводника и вблизи его поверхности. Электроёмкость уединённого проводника. Конденсаторы. Электроёмкость различных типов конденсаторов (плоский, сферический, цилиндрический). Последовательное и параллельное соединение конденсаторов.
Проводники – тела, в которых электрический заряд может перемещаться по всему объёму.
Проводники первого рода – металлы.
Проводники второго рода – расплавленные соли, растворы кислот.
Напряжённость поля внутри проводника: , , .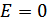
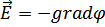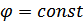Напряжённость поля вблизи поверхности проводника: , , , .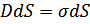
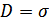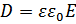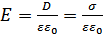Электроёмкость уединённого проводника определяется зарядом, сообщение которого проводнику изменяет его потенциал на единицу.
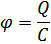Конденсатор – это устройство, которое при малых размерах и небольших, относительно окружающих тел, потенциалах могут накапливать (конденсировать) на себе значительные по величине заряды, т.е. обладают большой ёмкостью.
Электроёмкость плоского конденсатора: .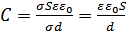
Электроёмкость сферического конденсатора: .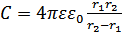
Электроёмкость цилиндрического конденсатора: .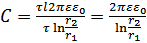
Параллельное соединение конденсаторов: .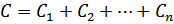
Последовательное соединение конденсаторов: .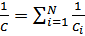

8. Энергия заряженного уединённого проводника и заряженного конденсатора. Энергия электростатического поля. Объёмная плотность энергии.
Энергия заряженного уединённого проводника: .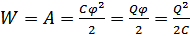
Энергия заряженного конденсатора: .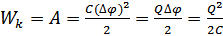
Энергия электростатического поля: .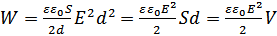
Объёмная плотность энергии: .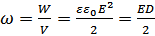

9. Постоянный электрический ток. Условия существования тока в проводнике. Характеристики тока.
Постоянный электрический ток – упорядоченное движение электрических зарядов.
Условия существования тока в проводнике:
1) Наличие в данной среде носителей заряда, которые могли бы перемещаться по проводнику.
2) Наличие внутри проводника электрического поля неэлектрического происхождения, энергия которого, каким-то образом восполняясь, расходовалась бы на перемещение зарядов.
Характеристики тока: сила тока и плотность тока.

10. Сторонние силы. Электродвижущая сила. Напряжение. Разность потенциалов.
Сторонние силы. Если в цепи на носители тока действуют только силы электростатического поля, то происходит перемещение носителей заряда от точек с большим потенциалом к точкам с меньшим потенциалом.
Электродвижущая сила. Для количественной характеристики введено понятие сторонних сил. Его характеризуют либо напряжённостью поля сторонних сил 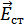, либо работой 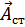, совершаемой сторонними силами при перемещении зарядов.
Напряжение – это физическая величина, определяемая работой, совершаемой суммарным полем электростатических (кулоновских) и сторонних сил при перемещении единичного положительного заряда на данном участке цепи.

11. Закон Ома для однородного участка цепи в интегральной и дифференциальной форме. Сопротивление и его зависимость от температуры. Сверхпроводимость.
Закон Ома: сила тока в цепи прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника: .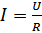
. .
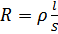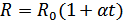Сверхпроводимость – свойство некоторых проводников, заключающееся в том, что их электрическое сопротивление скачком падает до нуля при охлаждении ниже определённой критической температуры 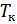, характерной для данного проводника.

12. Обобщённый закон Ома для неоднородного участка цепи в интегральной и дифференциальной форме. Анализ обобщённого закона Ома. Замкнутая электрическая цепь. Соединение сопротивлений: последовательное и параллельное.
. .
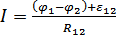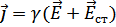Анализ закона Ома для замкнутой цепи: .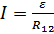
Последовательное соединение сопротивлений: .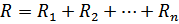
Параллельное соединение сопротивлений: .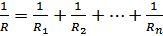

13. Работа и мощность тока. Закон Джоуля – Ленца в интегральной и дифференциальной форме.
Работа тока: .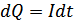
Мощность тока: .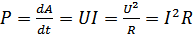
. .

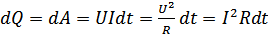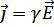14. Правила Кирхгофа для разветвлённых цепей. Узел. Правила для токов и Э.Д.С. при применении правил Кирхгофа.
Первое правило Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равно нулю.
Второе правило Кирхгофа: в любом замкнутом контуре, произвольно выбранном в разветвлённой электрической цепи, алгебраическая сумма произведений сил токов 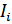на сопротивления 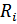соответствующих участков этого контура равна алгебраической сумме ЭДС 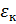, встречающихся в этом контуре: .
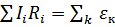Узел – точка, в которой сходится не менее трёх проводников с током.