Индивидуальное задание № 1
Министерство образования и науки
Российской Федерации
Федеральное государственное бюджетное образовательное
учреждение высшего профессионального образования
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра радиотехнических систем (РТС)
Пояснительная записка к индивидуальному заданию
по дисциплине "Теория электрической связи"
Студент гр. 1А1
___________ А.А. Загородников
___________
Руководитель
Доцент кафедры РТС
кандидат технических наук
______ ___________ А.С. Бернгардт
___________
Томск 2014
Индивидуальное задание № 1
1 Вероятностное описание символа
Для дискретной случайной величины X, принимающей одно из трех значений xj с вероятностями pj, записать ряд распределения и функцию распределения, привести соответствующие графики и найти следующие числовые характеристики: математическое ожидание и СКО, математическое ожидание модуля X, M[X 2], M[p(X)], M[(p(X))-1], M[-log2 p(X)].
Таблица 1.1 - Входные данные
| N | x1 | x2 | x3 | p1 | p2 | p3 |
| 52 | -9 | 2 | 9 | 0,06 | 0,71 | 0,23 |
Таблица 1.2 - Ряд распределения дискретной случайной величины
| xi | -9 | 2 | 9 |
| pi | 0,06 | 0,71 | 0,23 |
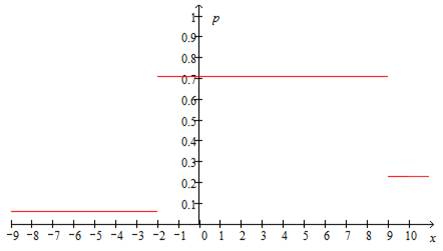
Рисунок 1.1 – Функция распределения дискретной случайной величины
Для расчета требуемых характеристик использовались следующие формулы:
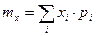 (1.1)
(1.1)
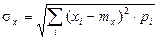 (1.2)
(1.2)
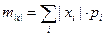 (1.3)
(1.3)
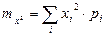 (1.4)
(1.4)
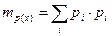 (1.5)
(1.5)
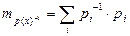 (1.6)
(1.6)
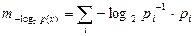 (1.7)
(1.7)
Таблица 1.3 - Полученные данные
| mx | s x | M [ | X | ] | M [ X 2 ] | M [ p ( X )] | M [( p ( X ))-1] | M [- log 2 p ( X )] | S |
| 0,11 | 5,13 | 4,03 | 26,33 | 0,561 | 3 | 1,082 | 40,243 |
2 Вероятностное описание двух символов
Два символа X и Y имеют возможные значения x1, x2 и y1, y2 соответственно. Задана матрица совместных вероятностей с элементами pj,k=p(xj , yk). Найти: ряд распределения случайной величины X а также mx, sx, M[-log2 p(X , Y)]. Повторить то же при каждом из условий Y = y1 и Y = y2, то есть определить условные ряды распределения и числовые характеристики случайной величины X.
Таблица 2.1 - Входные данные
| N | x 1 | x 2 | p 11 | p 21 | p 12 | p 22 |
| 52 | 3 | 6 | 0,24 | 0,35 | 0,11 | 0,3 |
Таблица 2.2 - Ряд распределения случайной величины Х
| xi | 3 | 6 |
| pi | 0,35 | 0,65 |
Для расчета требуемых характеристик использовались следующие формулы:
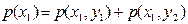 (2.1)
(2.1)
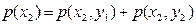 (2.2)
(2.2)
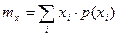 (2.3)
(2.3)
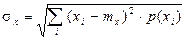 (2.4)
(2.4)
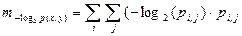 (2.5)
(2.5)
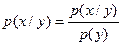 (2.6)
(2.6)
Таблица 2.2 - Полученные данные
| p(x1) | p(x2) | p(x1/y1) | p(x2/y1) | p(x1/y2) | p(x2/y2) | mx | sx | M[-log2 p(X,Y)] | S |
| 0,35 | 0,65 | 0,407 | 0,593 | 0,268 | 0,732 | 4,95 | 1,431 | 1,896 | 11,3 |
3 АЦП непрерывных сигналов
АЦП , m-разрядный рассчитан на входные напряжения в интервале (Umin , Umax) и проводит квантование во времени с шагом Dt=1. Записать последовательность, состоящую из 5 двоичных комбинаций на выходе АЦП, если на вход поступает сигнал U ( t )=u0+u1t+u2t2, для 0 ≤t≤4. Найти среднеквадратическую величину ошибки квантования по уровню для данного сигнала σ и затем ее теоретическое значение σo=Δu/(√12), где Δu – шаг квантования по уровню. Полученные двоичные комбинации представить в форме целых неотрицательных десятичных чисел Z0,Z1,…,Z4, например: 00011010=26. Построить графики фукции U(t) и погрешности восстановления сигнала ε(t).
Таблица 3.1 – Входные данные
| N | m | Umin | Umax | u 0 | u 1 | u 2 |
| 52 | 7 | -139.21 | -10.24 | -8.90 | -6.30 | -5.70 |
Для расчета требуемых характеристик использовались следующие формулы:
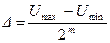 (3.1)
(3.1)
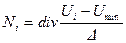 (3.2)
(3.2)
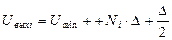 (3.3)
(3.3)
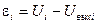 (3.4)
(3.4)
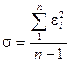 (3.5)
(3.5)
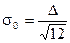 (3.6)
(3.6)
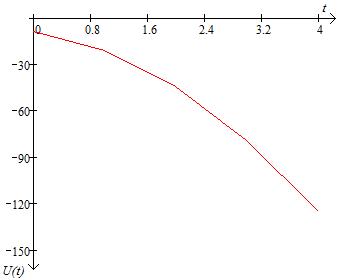
Рисунок 3.1 – Входной сигнал
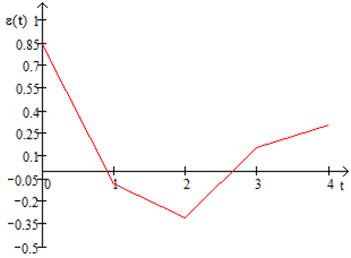
Рисунок 3.2 – Погрешность восстановления сигнала
Таблица 3.1 – Выходные данные
| Z 0 | Z 1 | Z2 | Z3 | Z 4 | σ | σo | S |
| 127 | 117 | 94 | 58 | 13 | 0,905 | 0,291 | 411,196 |
| 1111111 | 1110101 | 1011110 | 0111011 | 0001101 | |||
4 Нормальные случайные величины
Система случайных величин Х,У имеет нормальное распределение W ( x , y ), которое характеризуется вектором-строкой математических ожиданий a=(mx , my) и ковариационной матрицей K. Найти:sx, sy, коэффициент ковариации k; значение условного СКО sx(y) и математического ожидания mx(у); xmp(yo) – наиболее вероятное значение х при заданном уо; значение 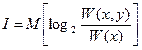 .
.
Таблица 4.1 – Входные данные
| N | mx | my | K 11 | K 22 | K 12 | y o |
| 52 | 3,86 | 3,08 | 1,62 | 3,14 | 1,93 | 5,98 |
Для расчета требуемых характеристик использовались следующие формулы:
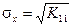 (4.1)
(4.1)
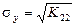 (4.2)
(4.2)
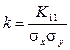 (4.3)
(4.3)
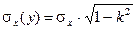 (4.4)
(4.4)
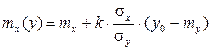 (4.5)
(4.5)
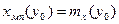 (4.6)
(4.6)
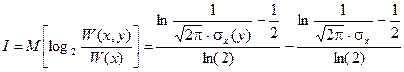 (4.7)
(4.7)
Таблица 4.1 – Выходные данные
| s x | s y | k | s x ( y о ) | I | xmp ( y o ) | S |
| 1,273 | 1,772 | 0,718 | 0,886 | 0,523 | 1,914 | 7,113 |








