Решение задания 2 (вариант решения)
Платежный календарь - план организации оперативной финансовой деятельности предприятия, в котором календарно взаимосвязаны все источники поступления денежных средств с расходами на осуществление финансово-хозяйственной деятельности. Форма платежного календаря произвольная, разрабатывается самим предприятием.
Платежный календарь (пример решения)
(Баланс доходов и расходов на февраль)
| № | Показатели | Объем (руб.) |
| 1 | Поступление денежных средств | |
| 1.1 | От реализации продукции | 216000 |
| 1.2 | Экспортные поступления | 66500 |
| 1.3 | От реализации ненужных товарно-материальных ценностей | 5150 |
| 1.4 | Прочая реализация | 7180 |
| Итого поступлений | 294830 | |
| 2 | Расходы денежных средств | |
| 2.1 | Косвенные налоги | 50970 |
| 2.2 | Оплата за материалы и комплектующие | 45680 |
| 2.3 | Заработная плата | 50800 |
| 2.4 | Отчисления в социальные фонды | 19500 |
| 2.5 | Электроэнергия | 2110 |
| 2.6 | Отопление | 13055 |
| 2.7 | Вода | 1000 |
| 2.8 | Связь | 140 |
| 2.9 | Ж/д транспорт | 2300 |
| 2.10 | Прочие налоги и сборы | 52450 |
| 2.11 | Гашение кредита и процентов банку | 14950 |
| 2.12 | Расходы на социальное развитие | 10700 |
| 2.13 | Расходы на производственные расходы | 32920 |
| 2.14 | Просроченная кредиторская задолженность | 610 |
| 2.15 | Прочие расходы | 2100 |
| Итого расходов | 299285 | |
| 3 | Балансирующие статьи | |
| 3.1 | Превышение поступлений над расходами | |
| 3.2 | Превышение расходов над поступлениями | 4455 |
| Коэффициент платежеспособности (Итого поступлений/Итого расходов) | 98,5 % | |
Т.к. коэффициент платежеспособности получился меньше единицы необходимо сбалансировать платежный календарь за счет не первоочередных расходов, перенеся их на следующий месяц. В качестве балансирующих статей затрат можно предложить расходы на социальное развитие, прочие расходы.
Решение задания 5
Примеры решения (т.к. экспертная оценка динамики отчетных данных и выбор базы для определения объема финансовых ресурсов на плановый квартал зависит от дополнительных факторов):
Выбрать один из вариантов решения и обосновать.
1. Анализ показывает, что предприятие работает неритмично в течение года. Потребность в ресурсах зависит от сезона. Исходя из этого, в качестве базы для определения объема финансовых ресурсов на плановый квартал примем среднюю величину ресурсов, потребляемых в аналогичном сезоне базисного года.
(180 + 200) / 2 = 190 тыс. руб.
190 * 1,2 = 228 тыс. руб.
2. В связи с неритмичностью работы, в качестве базы для определения объема финансовых ресурсов на плановый квартал можно принять и среднюю величину ресурсов, потребляемых в течение всего базисного года.
(180 + 100 + 120 + 200) / 4 = 150 тыс. руб.
150 * 1,2 = 180 тыс. руб.
3. В связи с неритмичностью работы, в качестве базы для определения объема финансовых ресурсов на плановый квартал можно принять объём использования финансовых ресурсов в аналогичном периоде базисного года.
180 * 1,2 = 216 тыс. руб.
4. В связи с неритмичностью работы, в качестве базы для определения объема финансовых ресурсов на плановый квартал можно принять объём использования финансовых ресурсов в предшествующем квартале базисного года.
200 * 1,2 = 240 тыс. руб.
4.4. «Демография»
Решение задания 1
Коэффициент роста за период t рассчитывается
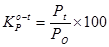
где: Р - численность населения;
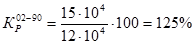
Коэффициент прироста за период t :
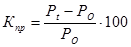 или
или 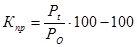
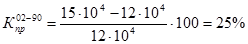
Среднегодовые темпы прироста за период t=12
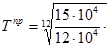 100 – 100 = 1,87%
100 – 100 = 1,87%
Можно сделать расчеты через «непрерывный» коэффициент прироста
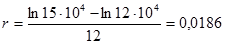 , тогда
, тогда
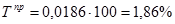
Решение задания 2
Вначале необходимо рассчитать среднее население за указанный период (год)
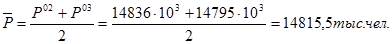
общий коэффициент рождаемости
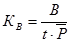 ;
;
где В- число родившихся в период t=1год.
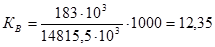 %о
%о
общий коэффициент смертности
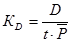 ;
;
где D- число умерших в период t=1 год.
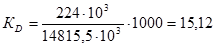 %о
%о
общий коэффициент абсолютного (общего) прироста

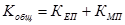
где 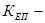 общий коэффициент естественного прироста
общий коэффициент естественного прироста 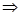
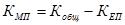
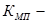 общий коэффициент механического (миграционного) прироста.
общий коэффициент механического (миграционного) прироста.
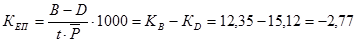 %о
%о
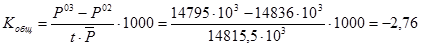 %о
%о
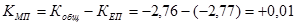 %о
%о
(Возможны другие алгоритмы решения задачи, но расчетные коэффициенты будут употреблены те же).
Решение задания 3
Средняя численность населения
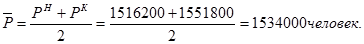
Общий коэффициент рождаемости
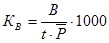 т.к. t=1 год, то в дальнейших формулах и расчетах t не ставим.
т.к. t=1 год, то в дальнейших формулах и расчетах t не ставим.
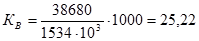 %о
%о
Общий коэффициент смертности
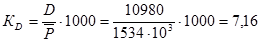 %о
%о
Общий коэффициент брачности
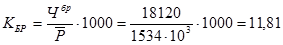 %о
%о
Общий коэффициент разводимости
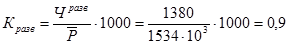 %о
%о
Общий коэффициент естественного прироста
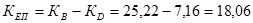 %о
%о
Общий коэффициент абсолютного (общего) прироста
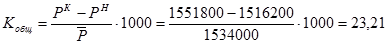 %о
%о
Общий коэффициент механического (миграционного) прироста
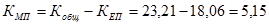 %о
%о
(Возможен другой алгоритм расчета коэффициентов естественного и механического приростов).
Решение задания 4
Средняя численность населения
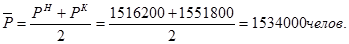
Общий коэффициент рождаемости 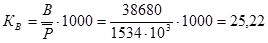 %о
%о
Специальный коэффициент рождаемости 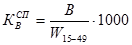 ;
;
где 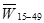 - среднегодовая численность женщин в возрасте от 15 до 49 лет (репродуктивный возраст).
- среднегодовая численность женщин в возрасте от 15 до 49 лет (репродуктивный возраст).
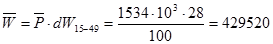 чел.
чел.
где 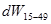 - для женщин репродуктивного возраста в общей численности.
- для женщин репродуктивного возраста в общей численности.
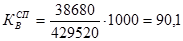 %о
%о
Решение задания 5
Коэффициент фертильности, он же специальный коэффициент рождаемости рассчитывается как:
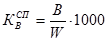 ;
;
Общий коэффициент рождаемости:
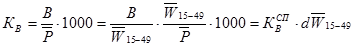 ;
;
где d 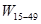 - доля женщин репродуктивного возраста 15-49 лет в общей численности населения.
- доля женщин репродуктивного возраста 15-49 лет в общей численности населения.
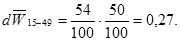
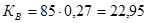 %о
%о
Решение задания 6
Вначале необходимо рассчитать коэффициент общего (общий коэффициент абсолютного) прироста.
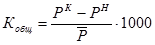
Средняя численность населения
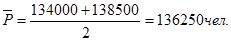
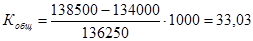 %о
%о
Коэффициент общего прироста равен сумме коэффициентов естественного и механического (миграционного) прироста, т.е.
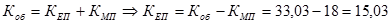 %о
%о
Коэффициент естественного прироста
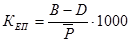
где В - число родившихся;
D - число умерших.
Тогда В = 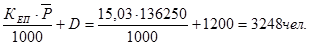
Решение задания 7
Коэффициент общего прироста
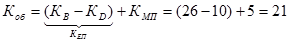 %о
%о
но 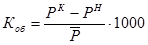 ;
;
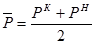
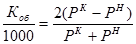 ;
;
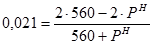 ;
;
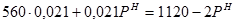 ;
;
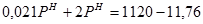 ;
;
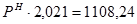
Численность на начало года
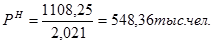
Темп роста 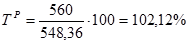
Темп прироста 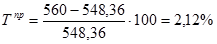
Решение задания 8
Вначале необходимо определить среднюю численность населения, которая в данном случае рассчитывается так:
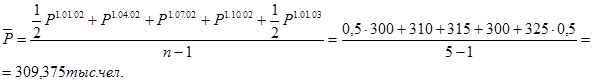 Коэффициент рождаемости
Коэффициент рождаемости
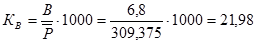 %о
%о
Коэффициент смертности
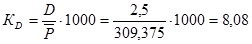 %о
%о
Коэффициент естественного прироста
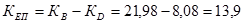 %о
%о
Коэффициент общего прироста
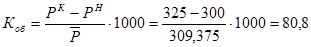 %о
%о
Коэффициент механического (миграционного) прироста
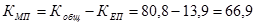 %о
%о
Решение задания 9
Суммарный коэффициент рождаемости рассчитывается:
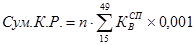 ;
;
где n-длина возрастного интервала;
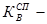 специальный коэффициент рождаемости.
специальный коэффициент рождаемости.
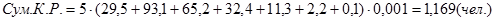
«Критическое значение» суммарного коэффициента рождаемости для РФ 2,12 ребенка; Т.о. зафиксированный уровень рождаемости обеспечивает простое воспроизводство на 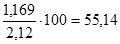 %
%
Решение задания 10
В начале необходимо рассчитать коэффициент непрерывного прироста численности населения:
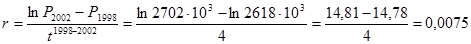
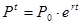 ;
;
где: 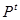 - прогнозируемаемая численность населения; t-длина прогнозного периода в годах.
- прогнозируемаемая численность населения; t-длина прогнозного периода в годах.
А так как 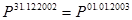 , то
, то
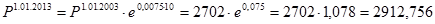 тыс. чел.
тыс. чел.
4.5. «Региональная экономика и управление»
Решение задания 1
Необходимо рассчитать фактическое значение коэффициента Джини 
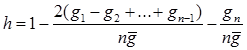
где gi - доход выделенного i–ого слоя населения;
n - количество выделенных слоев населения;
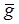 - совокупный доход населения.
- совокупный доход населения.
Но для расчетов необходимо выстроить ряд по возрастающей. Тогда фактическое значение
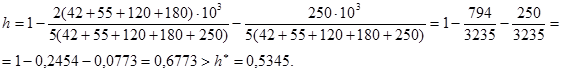
Фактическое значение больше нормативного, следовательно, неравенство доходов больше и методику в данном случае применять нельзя.
Решение задания 2
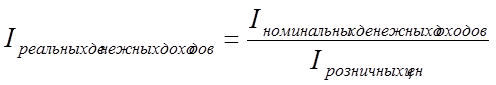

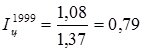 ;
; 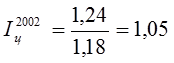 ;
;

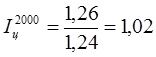 ;
; 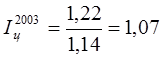 ;
;

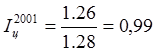 .
.
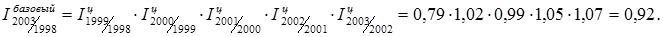
Условием задачи предусматривается комментарий полученных результатов.
Номинальные денежные доходы населения в регионе в период с 1999 года по 2003 год устойчиво росли, но в сопоставлении с темпом роста цен, роста реальных доходов до 2002 года не было. Только с 2002 года наблюдается незначительная тенденция роста реальных денежных доходов. Базовый же индекс свидетельствует о том, что на протяжении периода с 1999 по 2003 год реальные денежные доходы населения в регионе не увеличились, а уменьшились на 8%.
Решение задания 3
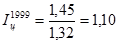 ;
; 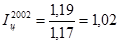 ;
;
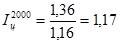 ;
; 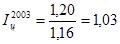 ;
;
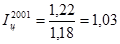 .
.
Расчет цепных индексов показывает изменение реального значения ВРП. В 1999-2000 годах рост был наибольшим (в 2000 году – 17%). Но с 2001 года рост реального ВРП резко замедлился и составлял всего 2%-3%. Об общем росте ВРП за период 1999 по 2003 год по сравнению с 1998 свидетельствует базовый индекс
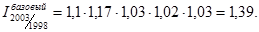
Т.е. общий рост реального значения ВРП составляет 39%.
Решение задания 4
Расчет штандортного веса и материального индекса необходим при использовании метода локационного (весового) многоугольника В.Лаунхардта.
Материальный индекс
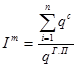
где 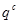 - вес сырья;
- вес сырья;
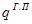 - вес готовой продукции;
- вес готовой продукции;
n – количество видов сырья.
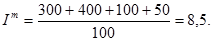

Штандортный вес
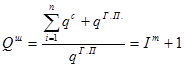
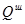 = 8,5 + 1 = 9,5.
= 8,5 + 1 = 9,5.
Решение задания 5
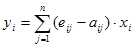
где yi – значение конечного спроса i –ой отрасли;
xi – валовые объемы выпуска i-ой отрасли;
а ij – коэффициенты прямых затрат продукции i-ой отрасли на производство единицы продукции j- ой отрасли;
eij – элементы единичной матрицы.
В матричной форме это выражение будет
Y = (E – A) . X
y1= (1-0,12) x1 + (0-0,3) x 2 + (0-0,15) x3
y1= (0-0,08) x1 + (1-0,2)2 + (0-0,15) x3
y 1 = (0-0,2) x 1 + (0-0,2) x 2 + (1-0,05) x 3
В 1-ом варианте задачи предусмотрено, что x1=20; x2=30; x3=20, тогда
y 1 = 0,88 . 20 + 0,3 . 30 – 0,15 . 20 = 5,6 (млрд.руб.)
y 2 = - 0,08 . 20 + 0,8 . 30 – 0,15 . 20 = 19,4 (млрд.руб.)
y 3 =-0,2 . 20 - 0,2 . 30 + 0,95 . 20 = 9 (млрд.руб.)
Решение задания 6
Для решения системы матричных уравнений можно представить в виде
X = ( E – A )-1 . Y или X = B . Y
Где X = ( xi ) – вектор-столбец валовых выпусков отраслей;
Y = ( yi ) - вектор-столбец конечной продукции;
В = ( bij ) – матрица коэффициентов полных затрат.
Уравнения межотраслевого баланса будут:
x1 = 1,25 . y1 + 0,54 . y2 + 0,28 . y3
x2 = 0,18 . y1 + 1,38 . y2 + 0,25 . y3
x3 = 0,3 . y1 + 0,4 . y2 + 1,16 . y3
x1 = 1,25 . 30 + 0,54 . 20 + 0,28 . 30 = 56,7 (млрд.руб.)
x2 = 0,18 . 30 + 1,38 . 20 + 0,25 . 30 = 40,5 (млрд.руб.)
x3 = 0,3 . 30 + 0,4 . 20 + 1,16 . 30 = 51,8 (млрд.руб.)
Решение задания 7
Значения прямых коэффициентов трудовых затрат определяются трудозатратами (чел.) на производство единицы (руб.) продукции отрасли j, т.е.,
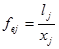
где lj - занятость в j –ой отрасли;
xj - валовой выпуск j –ой отрасли.
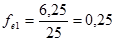 (чел./тыс.руб.)
(чел./тыс.руб.)
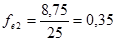 (чел./тыс.руб.)
(чел./тыс.руб.)
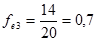 (чел./тыс.руб.)
(чел./тыс.руб.)
Коэффициенты полных трудовых затрат (Fej) представляют собой суммы затрат живого и овеществленного труда на единицу производственной продукции:
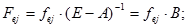
f e 1 = 1,25 . 0,25+ 0,18 . 0,35 + 0,3 . 0,7 = 0,5855 (чел./тыс.руб.)
f e 2 = 0,54 . 0,25+ 1,38 . 0,35 + 0,4 . 0,7 = 0,8980 (чел./тыс.руб.)
f e 3 = 0,28 . 0,25+ 0,25 . 0,35 + 1,16 . 0,7 = 0,9695 (чел./тыс.руб.)
Решение задания 8
Потребность в трудовых ресурсах (в матричной форме):
L = F . Y
где F – в нашем случае: вектор-строка коэффициентов полных затрат;
Y – вектор-столбец объемов конечного спроса отраслей.
L = 11,5 . 0,6+ 15 . 0,9 + 9 . 0,97 = 29,13 (млн.чел.)
Решение задания 9
Рассчитаем необходимые валовые отраслевые выпуски, обеспечивающие заданные значения объемов конечного спроса отраслей как: X = В . Y (векторно-матричная форма записи)
где В – матрица коэффициентов полных затрат;
Y – вектор-столбец значений конечного спроса отраслей.
x 1 = 1,19 . 3,5 + 0,4 . 35 + 0,21 . 18 = 21,945 < X 1 max =25 млрд.руб.
x 2 = 0,37 . 3,5 +1,36 . 35 + 0,33 . 18 = 54,835 < X 2 max =55 млрд.руб.
x 3 = 0,4 . 3,5 + 0,4 . 35 + 1,18 . 18 = 36,64 > X 3 max =35 млрд.руб.
Потребность в трудовых ресурсах рассчитаем как:
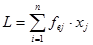 ;
;
где fej – коэффициенты прямых трудовых затрат.
L = 0,4 . 21,945 + 0,25 . 54,835 + 0,6 . 36,64 = 44,472 > Lmax =43,5 млн.чел.
Таким образом, данный прогнозный вариант не соответствует ограничениям по производственной мощности (превышение требуемого валового выпуска третьей отрасли на 1,64 млрд.руб. (36,6 – 35) и ограничениям по трудовым ресурсам на 0,972 млн.чел. (44,472 – 43,5).
Решение задания 10
Величины конечного спроса прогнозного варианта (yi) находятся из уравнений
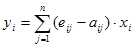 ,
,
путем постановки заданных величин валовых отраслевых выпусков (xi). Но величина конечного спроса каждой отрасли не может быть меньше значений предыдущего года.
y 1 = (1-0,05) . 22 + (0-0,25) . 52 + (0-0,1) . 38 = 4,1 > 3,5 млрд. руб.
y 2 = (0-0,2) . 22 + (1-0,15) . 52 + (0-0,2) . 38 = 32,2 > 32 млрд. руб.
y 3 = (0-0,25) . 22 + (0-0,2) . 52 + (1-0,05) . 38 = 20,2 > 14 млрд. руб.
Таким образом, величины конечного спроса всех отраслей прогнозного варианта больше значений предыдущего года.
Потребность в трудовых ресурсах рассчитывается как:
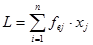 ,
,
где fej – коэффициенты прямых трудовых затрат.
L 1 = 0,4 . 22 + 0,25 . 52 + 0,6 . 38 = 44,6 > 44 млн. чел.
Т.е. прогнозный вариант не соответствует ограничениям по трудовым ресурсам на 0,6 млн. чел.








