Действия над векторами
Рассмотрим основные действия, определённые над векторами.
1. Сложение векторов. Суммой векторов 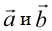 называют вектор
называют вектор 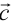 , который соединяет начало вектора
, который соединяет начало вектора 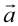 с концом вектора
с концом вектора 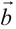 , при условии, что вектор
, при условии, что вектор 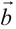 отложен от конца вектора
отложен от конца вектора 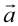 . Такой способ сложения векторов называют правилом треугольника.
. Такой способ сложения векторов называют правилом треугольника.
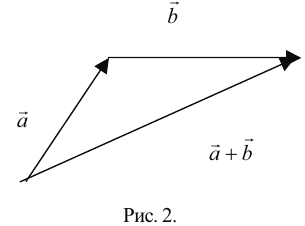
Учитывая, что 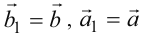 , то найти сумму векторов
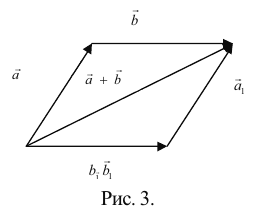
, то найти сумму векторов 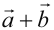 можно также по так называемым "правилом параллелограмма" (рис. 3)
можно также по так называемым "правилом параллелограмма" (рис. 3)
Вычитание векторов сводится к сложению противоположного вектора
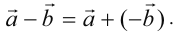
Запишем основные свойства действий сложения векторов:
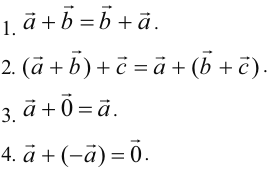
Заметим, что сумма нескольких векторов находится последовательным сложением двух из них, например:
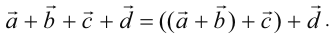
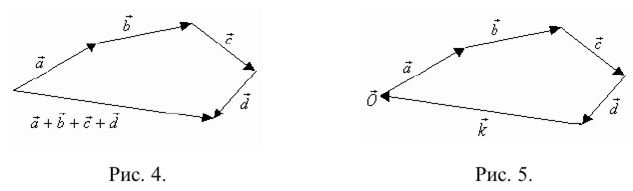
Геометрически сумма нескольких векторов находится их последовательным отложением один за одним так, чтоб начало следующего совпадало с концом предыдущего. Суммой является вектор, который будет соединять начало первого с концом последнего (рис. 4). Если такая последовательность векторов даёт замкнутую ломаную то суммой векторов является 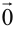 (рис. 5).
(рис. 5).
Умножение вектора на число
Произведением вектора 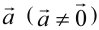 на число
на число 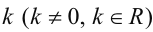 называют вектор
называют вектор 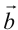 , для которого выполняются условия:
, для которого выполняются условия:
а) 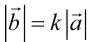 ;
;
б) 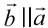 , причём
, причём 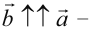 сонаправленные если
сонаправленные если 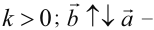 противоположно направленные, если
противоположно направленные, если 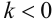 . Отсюда, очевидно, что необходимым и достаточным условием коллинеарности векторов является соотношение
. Отсюда, очевидно, что необходимым и достаточным условием коллинеарности векторов является соотношение 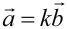 .
.
Запишем основные свойства действий умножения вектора на число:
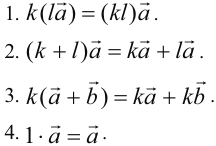
Скалярное произведение векторов
Скалярным произведением 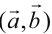 или
или 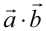 векторов
векторов 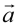 и
и 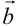 называют выражение
называют выражение 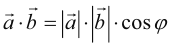 , где
, где 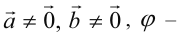 угол, который образуют векторы. Отметим, что углом между векторами считают угол между их направлениями. Если хотя бы один из векторов равен
угол, который образуют векторы. Отметим, что углом между векторами считают угол между их направлениями. Если хотя бы один из векторов равен 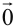 , то их скалярное произведение считают равным нулю.
, то их скалярное произведение считают равным нулю.
Очевидно, что скалярное произведение двух ненулевых векторов будет равно нулю тогда и только тогда когда эти вектора перпендикулярны (ортогональны). Действительно, если 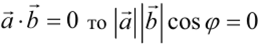 . Но
. Но 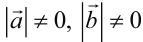 , следовательно,
, следовательно,
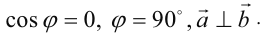
Наоборот, если 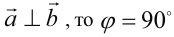 и согласно определениям
и согласно определениям
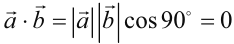 .
.
Например, скалярное произведение 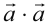 будет равным
будет равным
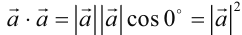
Запишем основные свойства действий скалярного умножения векторов:
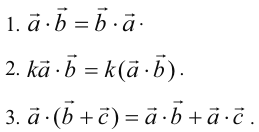
Домашнее задание:
· Записать в конспекте дату и тему занятия
· Внимательно изучить материал
· В конспект записать таблицу из лекции
· Выполненное домашнее задание прислать в ЛС преподавателю








