Занятие № 22 Тема. Вероятность события. Сложение вероятностей.

Дата: 2025-06-15; Просмотры: 1

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Мотивация изучения темы :

“В Москве на Болотной площади есть скульптура Михаила Шемякина “Дети в окружении пороков взрослых”. Там изображены 12 пороков”. “Но там нет еще одного – “Приобщения к азартным играм”.

Самый распространенный тип зависимости среди молодежи – это зависимость от игровых автоматов. Огромное количество подростков после школы, а то и вместо нее, бегут к “одноруким бандитам” в надежде выиграть энную сумму денег. Проигрывают, ищут возможности их найти, порой криминальные, чтобы опять скормить их груде металлолома”.

«Сегодня мы с вами начнем урок с игры. Во время игры попробуем ответить на вопрос: «Играть или не играть?».

Цели занятия :

Обучающие: дать определение понятию события и вероятности события;

получить новые знания о достоверных и невозможных событиях.

дать классическое определение вероятностей; теорема сложения вероятностей.

Развивающие: совершенствовать навыки самостоятельной работы студентов; формировать вероятностное мышление; развивать интерес к математике; развивать умение применять новый материал на практике и в жизни; активизировать мышление студентов.

Воспитательные: способствовать формированию коммуникативных навыков; способствовать формированию умения самостоятельно делать выводы, развивать речь.

Междисциплинарные связи: физика, история математики.

Список использованной литературы:

1.Алимов Ш.А. и др. Алгебра и начала анализа. 10 (11) кл. – М., 2012.

2.Башмаков М.И. Алгебра и начала математического анализа (базовый уровень).

3. Дополнительные источники: Интернет-ресурсы.

О, сколько нам открытий чудных
Готовят просвещенья дух
И опыт, сын ошибок трудных,
И гений, парадоксов друг,
И случай, бог-изобретатель...
А.С.Пушкин

Изучение новой темы
В стихотворении Пушкина к нашему уроку относятся два слова: опыт и случай. Что называется опытом или испытанием в теории вероятностей, что такое «случайное событие». Сегодня на уроке мы окунемся в загадочный мир Случая. Случай, случайность – с ними мы встречаемся повседневно: случайная ошибка, случайный выигрыш, случайная поломка. Случайности распоряжаются нами, подталкивают к каким-то действиям, подсказывают идеи.
Казалось бы, в царстве Случая нет места для математики – какие уж тут законы. Но и здесь наука обнаружила интересные закономерности, которые позволяют человеку уверенно чувствовать себя при встрече со случайными событиями.
Задача.
В коробке лежат 3 красных и 5 синих шариков. Какое наименьшее количество шариков, не глядя, нужно достать из коробки, чтобы среди них обязательно оказалось хотя бы 2 шарика одного цвета? (Ответ:3)
Итак, мы сделали свой выбор и решили задачу, которая была в домашнем задании у знакомой девочки – ученицы 3 класса. Умение не ошибиться и сделать правильный выбор – это качество, которому человек учится всю жизнь, приобретая жизненный опыт. Предлагаю вашему вниманию небольшую статью «В чем секрет успеха?»
Как-то раз молодой человек беседовал с успешным и состоятельным бизнесменом.
- Скажите, как вам удалось сколотить такое состояние? Раскройте свой секрет успеха.
- Мой секрет прост, - ответил собеседник, - всего два слова: правильные решения.
- Интересно, и что же помогает принимать вам эти решения?
- Тоже просто. Одно слово – опыт.
- Да, но как вы получаете этот опыт, - не унимался молодой человек.
- Проще простого, - улыбнулся успешный, - два слова: неправильные решения.
А вот французский философ Жан Буридан еще в ХIV веке придумал свой ставший знаменитым парадокс о голодном осле, оказавшемся на равном расстоянии от двух совершенно одинаковых охапок сена. История закончилась для осла трагически – он так и не смог сделать выбор, к какой из охапок направиться и, в конце концов, умер от голода. Выражением «буриданов осел» характеризуют и людей, потому что нам тоже случается попадать в ситуации, в которых нужно выбрать один из имеющихся равновозможных вариантов.
Попадали ли вы в такие ситуации? Что мы обычно делаем, если нужно выбрать один из двух вариантов? (бросаем монету, загадываем и смотрим, какой стороной она упадет)
А уж ученикам, надеюсь, эта ситуация до боли знакома, когда они решают, куда же пойти с yтpa: на занятия или гулять и бросают монету?
Все события или результаты опытов (наблюдений, испытаний) можно рассматривать как достоверные, невозможные и случайные. А изучается это в разделе математики, который называется “Теория вероятностей”.

События
результаты опытов, испытаний, наблюдений

1. Укажите среди данных событий случайные, достоверные, невозможные:

а) свалившийся со стола бутерброд упадет на пол маслом;

б) более двух попаданий в мишень при двух выстрелах;

г) не более двух попаданий в мишень при двух выстрелах;

д) в следующем году снег в Болотном не выпадет;

е) при бросании кубика выпадет четное число очков;

ж) в следующем году снег в Болотном выпадет.

Случайные события бывают совместными (несовместными), равновозможными (неравновозможными), элементарными (составными)

2. Какие пары событий совместные и какие несовместные?

а) идущий впереди человек работает инженером; идущего впереди человека зовут Иваном;

б) вышедший из библиотеки человек является офицером; вышедший из библиотеки человек – допризывник

в) наудачу взятая цифра кратна 5; наудачу взятая цифра больше 7;

г) наудачу взятое двузначное число окажется нечетным;

д) наудачу взятое двузначное число разделится на 73.
Всякое случайное событие является следствием многих причин. Поэтому невозможно заранее предсказать, произойдет единичное событие или нет. Но оказывается при многократном повторении опыта при одних и тех же условиях однородные случайные события подчиняются закономерностям, изучением которых и занимается теория вероятностей.
Знание этих закономерностей дает возможность прогнозировать события в массовых явлениях. Когда и как возникла эта наука?
Хотя ТВ, подобно другим наукам, возникла из потребностей практики (проблемы страхования, статистика заболеваемости, учет запасов продовольствия), исторически, как научная дисциплина, она сформировалась на материале теории азартных игр. Азартные игры так и создавались, чтобы исход был чисто случайным. Они удобны для изучения закономерности случайных событий, и возможность неограниченного повторения одной и той же игры обеспечивала экспериментальную проверку найденных законов в условиях массовости событий. (беседа о вреде азартных игр)
Основные понятия ТВ формировались в середине ХVП века в переписке между французскими учеными Паскалем и Ферма. При этом следует отметить, что выдающиеся ученые, решая различные задачи азартных игр, предвидели фундаментальную роль науки, изучающей случайные явления.
Из письма Б.Паскаля П.ФермаПариж, 19 ноября 1654 г, Г-ну ПьеруФерма,Тулуза.
"...В мире господствует случай и одновременно действует порядок и закономерность, которые формируются из массы случайностей, согласно законам случайного".
Само слово "азарт" французское и означает "случай". В конце ХVIII в. – начале XIX в. карточная игра сделалась своеобразной моделью жизни.

"Что ни толкуй Вольтер или Декарт –
Мир для меня колода карт,
Жизнь – банк; рок мечет, я играю,
И правила игры я к людям применяю".
М.Ю. Лермонтов

Да, что наша жизнь? Игра.
А есть ли среди вас азартные люди, любящие риск?
Я предлагаю вам игру. Будем бросать одновременно 2 игральных кубика и подсчитывать сумму выпавших очков. Если при очередной попытке в сумме выпадает 8 очков, то выигрываете вы, а если в сумме выпадает 7 очков, то побеждаю я. Справедлива ли моя игра? Одинаковы ли наши шансы на успех? Стоит ли вам рисковать? (решают задачу)
Давайте все вместе подсчитаем шансы на выигрыш у каждого игрока. Пусть событие
А – «при бросании 2 кубиков в сумме выпадет 8 очков»,
В – «при бросании 2 кубиков в сумме выпадет 7 очков».
Когда наступит событие А? Если выпадут цифры (2;6), (3;5), (4;4), (5;3), (6;2), т.е. благоприятствующими событию А будут 5 исходов, а событию B будут благоприятствовать следующие исходы: (1;6), (2;5), (3;4), (4;3), (5;2), (6;1), т.е. 6 событий.
А сколько всего равновозможных исходов? 36, и все они выпадают с одинаковыми возможностями (шансами).
Т.о., шансы на выигрыш вашего друга оцениваются как 5 из 36, т.е. 5/36, а у меня как 6 из 36 или 6/36=1/36. Следовательно, шансов выиграть у меня больше, и играть вашему другу с таким шулером опасно, т.к. игра не справедлива. Хотя может чисто случайно у него сразу с 1 опыта выпасть в сумме 8 очков, а у меня и после 10 бросков не выпасть. Но риск – благородное дело, и кто не рискует, тот не выигрывает.
В этой задаче мы подсчитывали шансы или степень возможности наступления какого-нибудь определенного события. Её и называют вероятностью события и обозначают буквой Р от английского слова probability – вероятность.
Т.о., возвращаясь к задаче, можно написать, что вероятность события А Р(А)=5/36, а вероятность события В Р(В)= 6/36=1/36.
Пусть n – общее число всех равновозможных несовместных исходов испытания,
m – число исходов, благоприятных событию А,
Р(А) – вероятность события А.
Какую формулу можно написать для вероятности события А? Подскажите, пожалуйста.

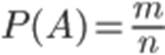
Это классическое определение вероятности события.
А теперь решим задачу, которую еще в ХVIII веке решал французский математик Д'Аламбер.
Вероятность любого события не может быть меньше нуля и больше единицы, т.е. 0≤P(A)≤1
Невозможному событию соответствует вероятность P(V)=0, а достоверному – вероятность P(U )=1

Теоремы сложения вероятностей.
Теорема сложения вероятностей несовместных событий.
Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

P(A+B)=P(A)+P(B);
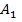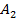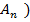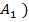P( + +…+ =P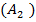( +P +…+P( ).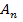

Теорема сложения вероятностей совместных событий.
Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:

P(A+B)=P(A)+P(B)-P(AB)

Для трех совместных событий имеет место формула:
P(A+B+C)=P(A)+P(B)+P(C)-P(AB)-P(AC)-P(BC)+P(ABC)

Событие, противоположное событию A (т.е. ненаступление события A), обозначают 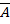. Сумма вероятностей двух противоположных событий равна единице: P(A)+P( 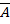)=1

События A,B,C,… называются независимыми, если вероятность каждого из них не меняется в связи с наступлением или ненаступлением других событий по отдельности или в любой их комбинации.

Пример.
Бросаются одновременно 2 монеты. Какова вероятность, что обе монеты упадут гербом кверху?
При решении задачи Д'Аламбер ошибся, так как считал, что равновозможны 3 события. Какие? Давайте перечислим: «выпали 2 герба», «выпали 2 цифры», «выпали герб и цифра». Но он не учел, что эти события неравновозможны, так как последнее событие происходит чаще двух других.
А на самом деле их 4: ГГ, ГЦ, ЦГ, ЦЦ. И событие А – «при бросании 2 монет выпадут два герба» произойдет с вероятностью не 1/3, а 1/4. Видите, какие могут быть нюансы. И следующая задача тоже с подвохом. За решение этой задачи можно сразу ставить «5».

Итак, мы научились находить вероятность в тех случаях, когда достоверное событие состоит из равновероятных возможностей. Однако часто возможности не равновероятны. Так, например, вы, наверное, замечали, что на уроках чаще спрашивают не совсем то, что вы учили, и не тогда, когда вы готовы к ответу. Впрочем, может быть, эти неприятные события нам лучше запоминаются, чем приятные.
Вашему вниманию предлагается следующая задача.

Со стола случайно упал бутерброд. Чему равна вероятность того, что он упадет маслом вниз? А маслом вверх?
Давайте, подсчитаем, используя классическое определение вероятности. Р=1/2.
А как на самом деле? Бутерброд падает маслом вниз чаще. Это так называемый закон бутерброда, по которому из двух возможных вариантов чаще реализуется наименее приятный (статья из журнала «Юный техник», №11,2001г.).

Вероятность суммы несовместных событий вычисляется по формуле

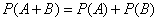
Задача 1.

Рассмотрим наш ящик. Там те же шары: 2 красных, 2 синих, 2 белых желтый и зеленый. Достали 1 шар. Найти вероятность того, что этот шар желтый или зеленый.

Решение. Р(А) = 1/8, Р(В) = 1/8, Р(А+В) = 1/8+1/8= ¼

Задача 2.
В лотерее из 1000 билетов имеются 200 выигрышных. Вынимают наугад один билет. Чему равна вероятность того, что этот билет выигрышный?
Решение: Событие A-билет выигрышный. Общее число различных исходов есть n=1000
Число исходов, благоприятствующих получению выигрыша, составляет m=200. Согласно формуле P(A)= 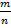, получим P(A)= 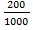= = 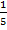0,2

Задача 3.
Из урны, в которой находятся 5 белых и 3 черных шара, вынимают один шар. Найти вероятность того, что шар окажется черным.
Решение: Событие A-появление черного шара. Общее число случаев n=5+3=8
Число случаев m, благоприятствующих появлению события A, равно 3
P(A)= 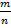= = 0,375

Д омашнее задание :

1. Изучить п. п.67,68 ,сделать опорный конспект

2. Посмотреть видео урок: https://www.youtube.com/watch?v=iFJL34-zNNM

https://www.youtube.com/watch?v=lHrnobZjkmY

https://www.youtube.com/watch?v=_dXEMtdD550

3. Решение задач. стр.345 № 1124-1128,1134-1140 четные

Самостоятельная работа:

1. В доме 100 квартир. Наугад выбирается одна из них. Какова вероятность того, что на двери выбранной квартиры вы увидите цифру 5?

2. Из 1000 собранных на заводе телевизоров 5 штук бракованных. Эксперт проверяет один наугад выбранный телевизор из этой 1000. Найти вероятность того, что проверяемый телевизор окажется бракованным.

3.В урне 9 красных, 6 желтых и 5 зеленых шаров. Из урны наугад достают один шар. Какова вероятность того, что этот шар окажется жёлтым?

4. Из 30 билетов, предлагаемых на экзамене, школьник может ответить только на 27. Какова вероятность того, что школьник не сможет ответить на наугад выбранный билет?

5. Имеются 20 карточек, на которых записаны числа от 1 до 20. Из них наугад выбирают одну карточек. Какова вероятность того, что на выбранной карточке будет число 20 или любое нечётное число?