Основные соотношения плоской задачи теории упругости
Уравнения плоской задачи теории упругости описывают упругое равновесие цилиндрических тел в случае плоской деформации, когда на тело действуют внешние силы, нормальные к его
оси и одинаковые для всех поперечных сечений, либо в случае обобщенного плоского напряженного состояния, т. е. при деформации тонкой пластинки силами, действующими в ее плоскости. Если тело отнесено к декартовой системе координат таким образом, что плоскость 
совпадает или с поперечным сечением стержня (плоская деформация) 
или со срединной плоскостью пластины (обобщенное плоское напряженное состояние), то для определения напряженно-деформированного состояния в произвольной точке упругого изотропного тела необходимо найти три компоненты тензора напряжений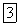 
и две составляющие вектора перемещений — 
являющиеся функциями двух переменных х и у.
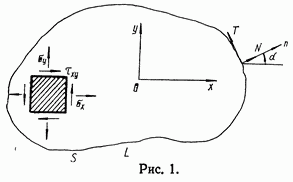
Рис. 1.
Известно, что при отсутствии объемных сил решение плоской задачи теории упругости сводится к интегрированию при определенных граничных условиях бигармонического уравнения
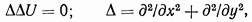
причем функция напряжений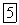 
связана с искомыми напряжениями 
следующим образом:
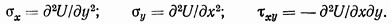
С помощью функций комплексного переменного общее решение уравнения (1.1) может быть выражено через две аналитические функции 
по формуле Гурса
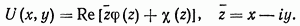
Компоненты напряжений 
и смещений 
связаны с комплексными потенциалами напряжений 
соотношениями [49]
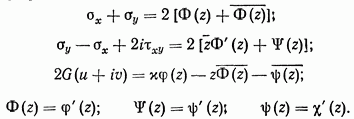
Здесь 
модуль сдвига; 
модуль Юнга; 
— коэффициент Пуассона; 
для плоской деформации и 
для обобщенного плоского напряженного состояния.
Решение плоской задачи теории упругости сводится к отысканию в области 
занятой телом, двух аналитических функций 
удовлетворяющих на границе тела определенным условиям. Когда на границе тела 
заданы напряжения (первая основная задача), граничное условие имеет вид
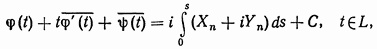
где 
координаты заданного на площадке с внешней нормалью 
вектора напряжений; 
переменная точка контура; 
соответствующая ей дуговая абсцисса; С — произвольная комплексная постоянная.
Когда на границе 
заданы перемещения (вторая основная задача), граничное условие следует непосредственно из соотношения (1.6):
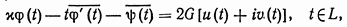
где 
известные, заданные на 
функции.
Граничные условия (1.7) и (1.8) основных задач теории упругости допускают и другую форму записи:
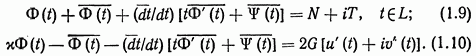
Здесь 
заданные нормальные и касательные компоненты усилия на границе тела;
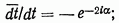
угол, образуемый внешней нормалью к контуру и осью 
(см. рис. 1).
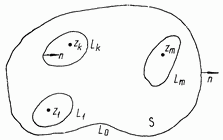
В случае многосвязной области 5 (рис. 2) функции 
в любой конечной ее части имеют вид
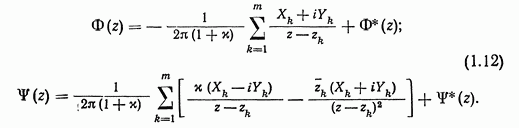
Здесь 
компоненты главного вектора внешних усилий, приложенных к самонепересекающемуся замкнутому контуру 
произвольная фиксированная точка внутри контура 
голоморфные в области 
функции 
соответствуют такому напряженному состоянию, когда главные векторы внешних усилий, действующих на контурах 
равны нулю.
Для бесконечной многосвязной области 
когда контур 
Целиком уходит в бесконечность (см. рис. 2), комплексные потенциалы 
можно представить в форме
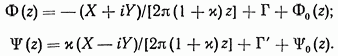
Здесь
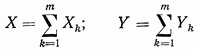
являются компонентами главного вектора внешних усилий, приложенных к границе области 
функции 
при больших 
имеют разложения
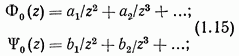
комплексные постоянные, характеризующие однородное напряженное состояние на бесконечности,
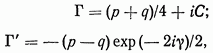
где 
главные напряжения, причем напряжения 
направлены под углом 7 к оси 
действительная постоянная С, обусловленная вращением на бесконечности, не влияет на распределение напряжений.
