Кішкене дөңгелек саңылаудағы Френель дифракциясы
К. дөңгелек саңылауға тоғысатын сәулелер түссін және саңлаудың Р нүктесіндегі жарық тербелесінің амплитудасын анықтайық (сурет). Френельдің алғашқы m-зонасынан келген жарық толқыны өтеді.
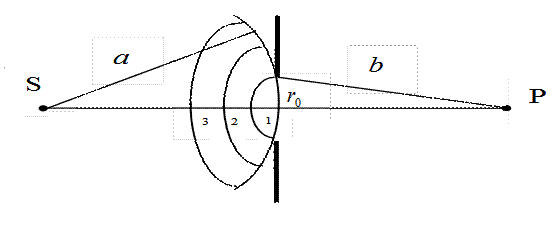
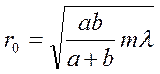 формуласынан саңлауға сиятын зоналар санын анықтаймыз, яғни
формуласынан саңлауға сиятын зоналар санын анықтаймыз, яғни 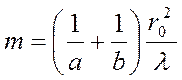 .
.
Р нүктесіндегі жарық тербелесінің амплитудасы 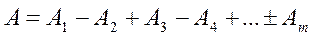 ,
,
мұндағы: 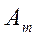 алдындағы таңба тақ зоналар үшін оң, жұп зоналар үшін теріс болып алынады.
алдындағы таңба тақ зоналар үшін оң, жұп зоналар үшін теріс болып алынады.
Егер саңлауға сиятын Френель зоналарының саны тақ болса,онда Р нүктесінде жарық күшейеді: 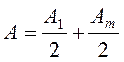 ;егер жұп болса, онда қарастырылатын Р нүктесінде жарық әлсірейді:
;егер жұп болса, онда қарастырылатын Р нүктесінде жарық әлсірейді: 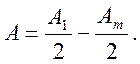
Дөңгелек мөлдір емес жағдайда дискі Френельдің алғашқы m зонасын жабады. Бұл Р нүктесіндегі
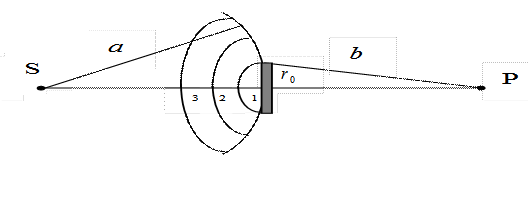
жарық тербелісінің амплитудасы 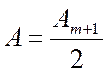 .
.
Р нүктесінде жарық тербелісі ашық тұрған бірінші зонаның тудыратын жарық тербелісінің амплитудасының жартысына тең болады, бұл нүктеде жарықтың ақ дағы көрінеді.
Шексіз ұзын бір саңлаудағы Фраунгофер дифракциясы
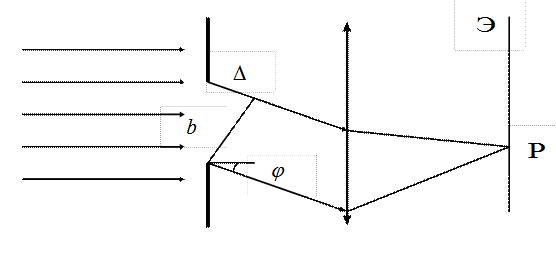
Интерференциялық көрініс алу үшін саңлаудың келесі бетіне саңлауға параллель жинағыш линза қойылып, линзаның фокустық жазықтығына экран қойылады. Шексіз ұзын саңлауға жазық толқын түскен жағдайда экранда кезектескен ақ және қоңыр жолақтар түріндегі интерференциялық көрініс алынады.Экрандағы Р нүктесінде төмендегі шарттар орындалғанда жарық күшейеді: 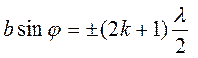 ,мұндағы:
,мұндағы: 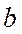 -саңлаудың ені, k-интерференциялық көріністің реті,
-саңлаудың ені, k-интерференциялық көріністің реті, 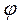 -сәулелердің ауытқу бұрышы.Р нүктесінде төмендегі шарттар орындалғанда жарық әлсірейді:
-сәулелердің ауытқу бұрышы.Р нүктесінде төмендегі шарттар орындалғанда жарық әлсірейді: 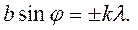
15.Дифракциялық тор және оның спектрлік сипаттамасы.
Жарықтың дифракциясы деп жарық толқындарының жолында кездесетін бөгеттерді айналып өтуін айтады.
Дифракциялық тор деп бiр-бiрiне жақын, әрi параллель орналасқан тар жолақ саңлаулар жүйесiнен тұратын спектральдық құралды айтады (1- сурет ).
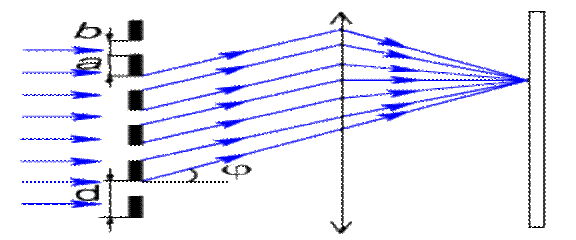
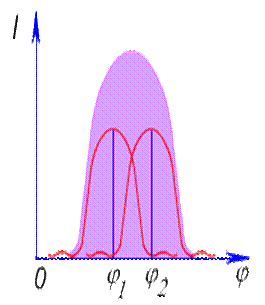
Мұндағы a - күңгiрт жолақтың енi, b – саңлаудың енi, ал d=a+b– дифракциялық тордың тұрақтысы деп аталады. Қазiргi кезде қолданылатын дифракциялық торлардың бiр миллиметрiне 2000–ға дейiн саңлаулар салынады. Гюйгенс-Френель принципiне сәйкес мұндай әрбiр саңлау өз кезегiнде жаңа когеренттi толқын көздерi болып табылады да бұл көзден туындылаған толқындар бiр-бiрiмен интерференцияланады.Егер дифракциялық торға перпендикуляр бағытта параллель жарық сәулелерi түсетiн болса, онда линзаның фокальдық жазықтығында орналасқан экранда қандай да бiр φ бұрышымен дифракциялық максимумдар байқалады.
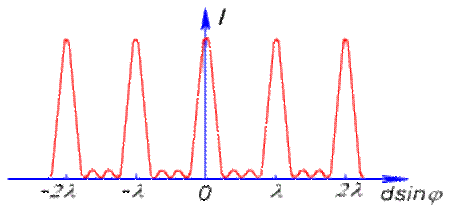 2 - сурет
2 - сурет
2- суреттен көрiнiп тұрғанындай бұл максимумдар мынадай шарттарды қанағаттандырады: d sinφ = n λ
мұндағы n=0, 1, 2, … - бас
 3- сурет
3- сурет
|
максимумдар рет i деп аталады.
Дифракциялық торлар жарықты спектрлерге жiктеу үшiн, сонымен қатар жарықтың белгiсiз толқын ұзындығын анықтау үшiн де қолданылады. Нақтылы зерттеулерде бiр өлшемдi торлармен қатар екi өлшемдi торлар да жиi қолданылады. Екi өлшемдi торлар деп жолақтарын бiр-бiрiне перпендикуляр орналастырып, беттестiрген екi жәй тордан тұратын жүйенi айтады. Мұндай жүйеден өткен жарық 3- суреттегiдей болып дифракцияланады.
16.Жарық толқынының дисперсиясы
Заттың n сыну көрсеткішінің электромагниттік толқынның 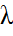 толқын ұзындығына (немесе
толқын ұзындығына (немесе 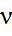 жиілігіне) тәуелділігі әлде бұған сәйкес ортадағы
жиілігіне) тәуелділігі әлде бұған сәйкес ортадағы 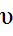 жылдамдықтың
жылдамдықтың 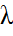 -ға (немесе
-ға (немесе 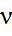 жиілігіне ) тәуелділігі электромагниттік толқынның (жарықтың) дисперсиясы деп аталады.
жиілігіне ) тәуелділігі электромагниттік толқынның (жарықтың) дисперсиясы деп аталады.
Сонымен, электромагниттік толқынның (жарықтың) дисперсия құбылысы n=n( 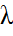 ) [n=n(
) [n=n( 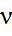 )] немесе
)] немесе 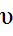 =
= 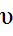 (
( 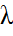 ) [
) [ 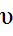 =
= 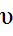 (
( 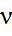 )] функциялық тәуелділіктерінің болатындығын білдіреді.
)] функциялық тәуелділіктерінің болатындығын білдіреді.
Электроманиттік толқындардың дисперсиясы байқалатын орталар дисперсиялаушы орталар деп аталады. 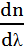 немесе
немесе 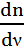 туындысымен анықталатын физикалық шама зат дисперсиясы деп аталады, ол дисперсиялаушы ортаны сипаттайтын шама. Әдетте тәжірибеде толқын ұзындығы өскенде ортаның сыну көрсеткішінің кішіреюі (немесе түсетін толқынның жиілігі өскенде сыну көрсеткішінің өсуі) байқалады. Осындай дисперсия
туындысымен анықталатын физикалық шама зат дисперсиясы деп аталады, ол дисперсиялаушы ортаны сипаттайтын шама. Әдетте тәжірибеде толқын ұзындығы өскенде ортаның сыну көрсеткішінің кішіреюі (немесе түсетін толқынның жиілігі өскенде сыну көрсеткішінің өсуі) байқалады. Осындай дисперсия 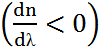 қалыпты дисперсия деп аталады. Кейбір жағдайларда, керісінше түсетін жарықтың толқын ұзындығы кішірейгенде, яғни тербеліс жиілігі артқанда сыну көрсеткішінің кемуі байқалады – бұл аномаль дисперсия
қалыпты дисперсия деп аталады. Кейбір жағдайларда, керісінше түсетін жарықтың толқын ұзындығы кішірейгенде, яғни тербеліс жиілігі артқанда сыну көрсеткішінің кемуі байқалады – бұл аномаль дисперсия 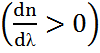 деп аталады.
деп аталады.
n( 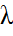 ) тәуелділігін теориялық жолмен алуға бірнеше рет әрекет жасалған. 19 ғ.-да атақты математика Коши Френельдің көріністеріне сүйеніп мына формуланы ұсынды:
) тәуелділігін теориялық жолмен алуға бірнеше рет әрекет жасалған. 19 ғ.-да атақты математика Коши Френельдің көріністеріне сүйеніп мына формуланы ұсынды: 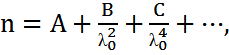
Мұндағы 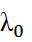 - вакуумдық толқын ұзындығы; А, В, С – тәжірибеде анықталатын тұрақтылар.
- вакуумдық толқын ұзындығы; А, В, С – тәжірибеде анықталатын тұрақтылар.
17.Электромагнит толқындардың поляризациялануы
Электромагниттік толқындардың, жарық толқынының да, көлденең толқындар екендігі белгілі: жарық толқыны электр және магнит өрістерінің Е, Н кернеуліктері өзара перпендикуляр, әрі жарық сәулесі бағытына (k толқындық векторға немесе толқынның таралу жылдамдығына) перпендикуляр жазықтықта тербеліс жасайды. Е, Н және k векторлары оң бұрандалық жүйе құрап тұрады. Сондықтан, егер толқынның бағыты (k) және кернеулік векторларының (E немесе H) біреуінің бағыты белгілі болса, онда басқа кернеуліктің бағытын анықтау қиын емес. Әдетте электормагниттік толқынның электр өрісінің Е кернеулігі ғана қарастырылады және оны жарық векторы деп атайды.
Жарықты электромагниттік толқын ретінде сипаттайтын құбылыстардың бірі – жарықтың поляризациясы.
Поляризацияланған жарық деп Е жарық векторының тербелісі белгілі бір бағытта реттелген жарық толқынын айтады. Табиғи жарықта (Күннің жарығы, электр шамының жарығы және т.т.) жарық векторының тербелістері ортаның кез келген нүктесінде барлық мүмкін болатын бағыттарда, бірін-бірі тез, әрі бейберекет алмастырып отырып жасалады.
Егер Е векторының тербелістері сәуле арқылы өтетін тек бір жазықтықта жасалатын болса, онда толқын жазық поляризацияланған толқын болады. Е векторы тербеліс жасайтын жазықтық поляризация жазықтығы деп аталады.
Егер қандай да бір поляризациялық аспап жазық поляризацияланған сәулені алу үшін қолданылатын болса, онда ол поляризатор деп, ал егер осы аспап поляризацияланған сәулені зерттеу үшін пайдаланылса – анализатор деп аталады.
Поляризаторға интенсивтігі І0 жазық поляризацияланған сәуле түседі дейік; және поляризатордың өткізу жазықтығы түсетін сәуленің Е0 векторының тербеліс жазықтығымен α бұрыш жасайтын болсын. (1-сурет). Түсетін жазық поляризацияланған сәуледегі электрлік тербелістердің
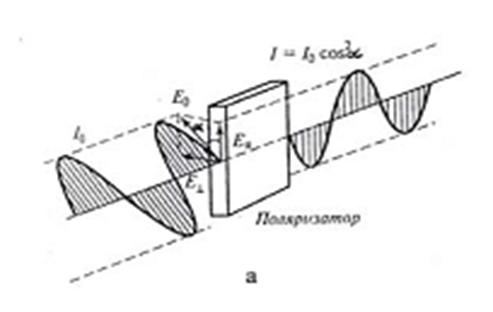
Е0 амплитудасын ЕІІ = E0 cosα және E┴ = E0 sinα екі құраушыға жіктейміз. Поляризатор арқылы бірінші тербеліс (ЕІІ ) өтеді, ал екінші тербеліс (E┴) өтпейді. Поляризаторға түсетін толқын интенсивтігі амплитуда квадратына пропорционал (І0 ~ Е02 ) болатындықтан, поляризатор арқылы өткен толқын интенсивтігі ЕІІ-тың квадратына пропорционал (І ~ ЕІІ2) болады, яғни
ЕІІ2 = E02 cos2α → I = I0 cos2α (1) (1)қатысы Малюс заңы деп аталады, оны 1810ж. Француз физигі Э.Малюс тапқан.
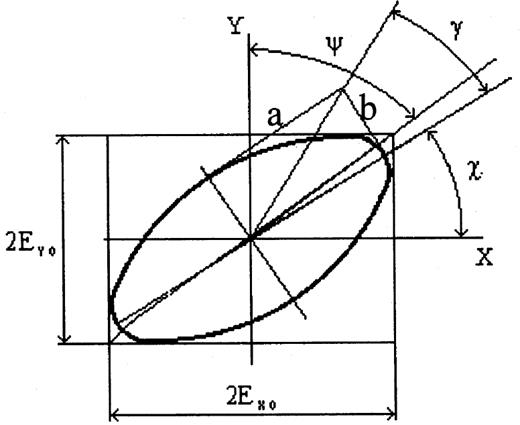
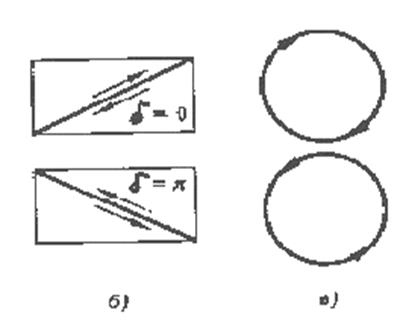
18.Жазық гармоникалық толқынның поляризация күйлері. Эллипстік, дөңгелек, сызықтық поляризациялар





поляризация).
19.Жарықтың анизатропты орталарда таралуы



20.Жарық сәулелерінің қосарланып сынғанда поляризациялануы


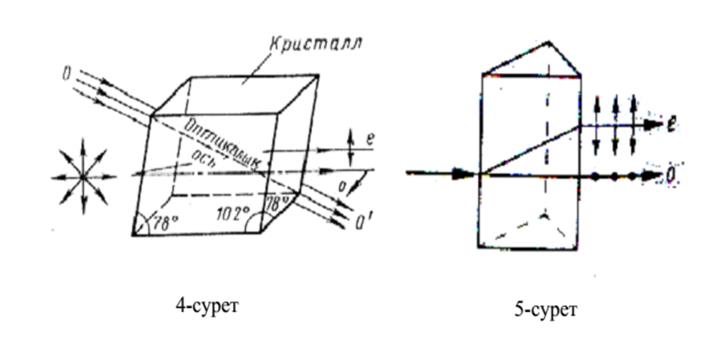

21.Поляризацияланған жарықты алу. Поляризаторлар.
Жарықты электромагниттік толқын ретінде сипаттайтын құбылыстардың бірі – жарықтың поляризациясы.
Поляризацияланған жарық деп Е жарық векторының тербелісі белгілі бір бағытта реттелген жарық толқынын айтады. Табиғи жарықта (Күннің жарығы, электр шамының жарығы және т.т.) жарық векторының тербелістері ортаның кез келген нүктесінде барлық мүмкін болатын бағыттарда, бірін-бірі тез, әрі бейберекет алмастырып отырып жасалады.
Егер Е векторының тербелістері сәуле арқылы өтетін тек бір жазықтықта жасалатын болса, онда толқын жазық поляризацияланған толқын болады. Е векторы тербеліс жасайтын жазықтық поляризация жазықтығы деп аталады.
Егер қандай да бір поляризациялық аспап жазық поляризацияланған сәулені алу үшін қолданылатын болса, онда ол поляризатор деп, ал егер осы аспап поляризацияланған сәулені зерттеу үшін пайдаланылса – анализатор деп аталады.
Поляризаторға интенсивтігі І0 жазық поляризацияланған сәуле түседі дейік; және поляризатордың өткізу жазықтығы түсетін сәуленің Е0 векторының тербеліс жазықтығымен α бұрыш жасайтын болсын. (1-сурет). Түсетін жазық поляризацияланған сәуледегі электрлік тербелістердің
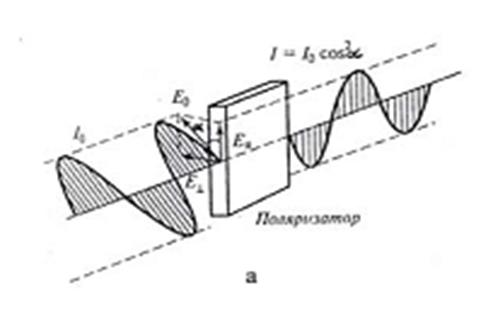
Е0 амплитудасын ЕІІ = E0 cosα және E┴ = E0 sinα екі құраушыға жіктейміз. Поляризатор арқылы бірінші тербеліс (ЕІІ ) өтеді, ал екінші тербеліс (E┴) өтпейді. Поляризаторға түсетін толқын интенсивтігі амплитуда квадратына пропорционал (І0 ~ Е02 ) болатындықтан, поляризатор арқылы өткен толқын интенсивтігі ЕІІ-тың квадратына пропорционал (І ~ ЕІІ2) болады, яғни
ЕІІ2 = E02 cos2α → I = I0 cos2α (1)
(1)қатысы Малюс заңы деп аталады, оны 1810ж. Француз физигі Э.Малюс тапқан.
22.Поляризацияланған толқындардың интерференциясы
23.Жарықтың заттағы қалыпты және аномаль дисперсиясы.
Заттың n сыну көрсеткішінің электромагниттік толқынның 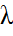 толқын ұзындығына (немесе
толқын ұзындығына (немесе 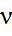 жиілігіне) тәуелділігі әлде бұған сәйкес ортадағы
жиілігіне) тәуелділігі әлде бұған сәйкес ортадағы 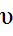 жылдамдықтың
жылдамдықтың 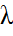 -ға (немесе
-ға (немесе 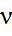 жиілігіне ) тәуелділігі электромагниттік толқынның (жарықтың) дисперсиясы деп аталады.
жиілігіне ) тәуелділігі электромагниттік толқынның (жарықтың) дисперсиясы деп аталады.
Сонымен, электромагниттік толқынның (жарықтың) дисперсия құбылысы n=n( 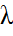 ) [n=n(
) [n=n( 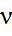 )] немесе
)] немесе 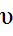 =
= 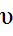 (
( 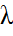 ) [
) [ 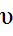 =
= 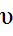 (
( 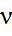 )] функциялық тәуелділіктерінің болатындығын білдіреді.
)] функциялық тәуелділіктерінің болатындығын білдіреді.
Электроманиттік толқындардың дисперсиясы байқалатын орталар дисперсиялаушы орталар деп аталады. 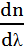 немесе
немесе 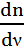 туындысымен анықталатын физикалық шама зат дисперсиясы деп аталады, ол дисперсиялаушы ортаны сипаттайтын шама. Әдетте тәжірибеде толқын ұзындығы өскенде ортаның сыну көрсеткішінің кішіреюі (немесе түсетін толқынның жиілігі өскенде сыну көрсеткішінің өсуі) байқалады. Осындай дисперсия
туындысымен анықталатын физикалық шама зат дисперсиясы деп аталады, ол дисперсиялаушы ортаны сипаттайтын шама. Әдетте тәжірибеде толқын ұзындығы өскенде ортаның сыну көрсеткішінің кішіреюі (немесе түсетін толқынның жиілігі өскенде сыну көрсеткішінің өсуі) байқалады. Осындай дисперсия 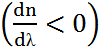 қалыпты дисперсия деп аталады. Кейбір жағдайларда, керісінше түсетін жарықтың толқын ұзындығы кішірейгенде, яғни тербеліс жиілігі артқанда сыну көрсеткішінің кемуі байқалады – бұл аномаль дисперсия
қалыпты дисперсия деп аталады. Кейбір жағдайларда, керісінше түсетін жарықтың толқын ұзындығы кішірейгенде, яғни тербеліс жиілігі артқанда сыну көрсеткішінің кемуі байқалады – бұл аномаль дисперсия 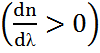 деп аталады.
деп аталады.
n( 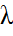 ) тәуелділігін теориялық жолмен алуға бірнеше рет әрекет жасалған. 19 ғ.-да атақты математика Коши Френельдің көріністеріне сүйеніп мына формуланы ұсынды:
) тәуелділігін теориялық жолмен алуға бірнеше рет әрекет жасалған. 19 ғ.-да атақты математика Коши Френельдің көріністеріне сүйеніп мына формуланы ұсынды: 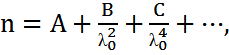
Мұндағы 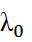 - вакуумдық толқын ұзындығы; А, В, С – тәжірибеде анықталатын тұрақтылар.
- вакуумдық толқын ұзындығы; А, В, С – тәжірибеде анықталатын тұрақтылар.
24.Жарықтың жұтылуы және шашырауы. Бугер заңы.
Жазық жарық толқыны затта таралған кезде оның интенсивтілігі біртіндеп азая бастайды. Бұл жарықтың затта жұтылу құбылысы д.а
Бугер заңы - жарықтың параллел монохроматты шоғының жұту қабілеті бар заттық ортада тарау барысында бiртiндеп әлсiретуiн анықтайтын заң.
Интенсивтігі І0 жарықтың параллель шоғы қалыңдығы мөлдір біртекті ортаның бетіне нормаль бағытталған болсын. Жұтылу нәтижесінде ортадан шыққан шоқтың интенсивтігі кемиді (оны І арқылы белгілейміз). Заттың берілген қабатында жұтылу заңдылығын анықтау керек.
Координаттар басын ортаның алдыңғы бетіне орналастырып, у осін осы бетке параллель бағыттаймыз, ал х осін – жарықтың таралу бағыты бойымен бағыттаймыз (1- сурет).
 y
y
 l
l
 |

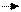




 dx
dx




 I0 I
I0 I
 |  | ||||||
 | |||||||
 | |||||||

 x
x
Затта шексіз жіңішке қалыңдығы dx қабатты ойша бөліп аламыз. Қалыңдығы dx қабаттағы жарық интенсивтігінің кемуі осы қабатқа түсетін интенсивтіктің шамасына және жқтушы қабат қалыңдығына пропорционал, яғни
dI = - αIdx (1)
мұндағы α – жарық интенсивтігіне тәуелсіз, пропорционалдық коэффициент. Минус таңбасы жұтатын қабаттың қалыңдығы артқан сайын ол арқылы өтетін жарық интенсивтігінің кемитіндігін көрсетеді.
Қалыңдығы l қабаттан шығатын жарықтың интенсивтігі өрнегін алу үшін (1) өрнекті 0-ден l –ге дейінгі аралықта интегралдаймыз:
∫ dI / I = - ∫ αdx
Ортаның біртектілігіне және әрбір қабатта түсетін энергияның бірдей бөлігі жұтылатындығына байланысты ортаның жұтылу қабілетін сипаттаушы коэффициент, х координаттан да, интенсивтіктен де тәуелді болмайды. Демек, оны тұрақты ретінде интеграл астынан шығару,а болады. Сонда мынаны аламыз:
ln I – ln I0 = - αl
Осыдан
I = I0 e-αl (2)
мұндағы І0 және І – ортаның бетіне түсетін және қалыңдығы l қабаттан шығатын жарық интенсивтігі, α – жұтылу коэффициенті.
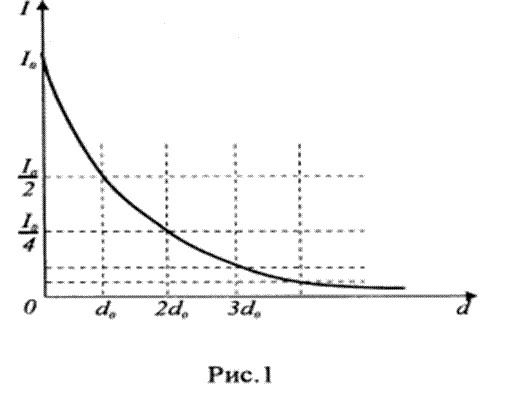
(2)формуланы 1729ж. Бугер тағайындап негіздеген, сондықтан Бугер заңы деп аталады.
Жұтылу коэффициентінің (α) сандық мәні l/ α мәніне тең d-қабаттың қалыңдығына сәйкес келеді және одан өткеннен кейін оның интенсивтілігі e=2,72 есеге азаяды. Бұл заңдылық заттағы жарық толқынының интенсивтілігі экспонента бойынша азаятынын көрсетеді. Егер жарық қалыңдығы d болатын материалдан өткен кезде оның интенсивтілігі N ретке азайса, қалыңдығы 2d болатын материалдан өткен кезде N2 ретке азаяды.
25.Жылулық сәуле шығару және оның негізгі заңдары.
Сәулеленуші дененің ішкі энергиясы есебінен пайда болатын және тек дененің температурасы мен химиялық қасиеттеріне байланысты электромагниттік сәулелену жылулық сәулелену деп аталады.
Дене температурасының абсолют нөлден өзгешеленетін температураларда заттың молекулалары мен атомдарының жылулық қозғалысымен түсіндірілетін электромагниттік сәуле шығаруды дененің жылулық сәуле шығаруы деп атаймыз.
Жылулық сәуле шығару тұтас спектрге ие, алайда ондағы энергияның таралуы температурадан тәуелді: төменгі температураларда жылулық сәуле шығару инфрақызыл, ал жоғары температураларда көрінетін және ультракүлгін спектрлеріне басым болады.
Жылулық сәуле шығарудың басқа сәуле шығарулардан өзгешелігі ол – тепе-теңдікті сәуле шығару болып табылады, яғни изоляцияланған жүйеде дене берілген температурада (абсолют нөлден өзгеше) уақыттың өтісімен дене мен оның сәуле шығаруының арасында динамикалық жылулық тепе-теңдік орнатылады.
Жылулық сәуле шығарудық негізгі сипаттамалары:
а) Сәуле шығару ағыны Ф – бірлік уақыт аралығында қуаттың орташа мәніне тең болатын физикалық шама. СИ жүйесінде сәуле шығару ағыны ваттпен (Вт) өлшенеді.
Ф = E/t
б) Дененің энергетикалық жарықтылығы Re - қыздырылған дененің бірлік ауданнан шығарылатын сәуле шығарудың ағынына тең физикалық шама. СИ жүйесінде сәулешығару ағаны (Вт/м2) өлшенеді.
Re = Ф/S = E/St
в)Жұту коэффициенті α (берілген температурада дененің электромагниттік энергияны жұту қабілетін сипаттайтын шама) – берілген дененің жұтқан жарық ағынының осы денеге түскен жарық ағынына қатынасына тең физикалық шама:
α = Фпогл / Фпад
Барлық жиіліктер аймағында жұту коэффициенті 1-ге тең дене абсолютті қара дене деп аталады. Ол өзіне түскен барлық сәулені жұтады.
Рэлей және Джинс өрнегі
Ε (v, T) = (2πv2 / c2)kT
Абсолют қара дененің сәуле шығарғыштық қабілеті үшін Рэлей және Джинс өрнегі тек төменгі жиілік немесе ұзын толқын аумақ үшін ғана дәл келеді.
Планк өрнегі.
ε (v, T) = 2πv2 /c2 * hv/ ehv/kT – 1
Абсолют қара дененің сәуле шығарғыштық қабілеттілігі үшін алынған Планк өрнегі әртүрлі температуралар кезінде тәжірибемен өте жақсы сәйкес келеді.
Кирхгоф заңы.
Дененің сәуле шығарғыштық қабілеттілігінің оның жұтқыштық қабілеттілігіне қатынасы дененің химиялық құрамына тәуелді болмайды және ол абсолют қара дененің сәуле шығарғыштық қабілеттілігі болып, ол температура мен жиіліктің f (v, T) функциясы болып табылады.
E (v, T) / A (v, T) = ε (v, T)
Абсолют қара дененің жұтқыштық қабілеті A (v, T) =1
Абсолют қара дене үшін E (v, T) = ε (v, T) болады.
Больцман заңы.
Абсолют қара дененің энергетикалық жарқырауы абсолют температураның төрт дәрежесіне пропорционал болады. Абсолют қара дененің энергетикалық жарқырауы E (v, T) = ε (v, T) сәуле шығарғыштық қабілеттілігіне тең болады.
ε (T) = σT4
мұндағы σ=5,67*108 (Вт/м2к4) – пропорционалдық коэффициенті Стефан-Больцман тұрақтысы деп аталады.
Виннің ығысу заңы.
Абсолют қара дененің сәуле шығарғыштық қабілеттілігінің максимум мәніне келетін жиілік оның абсолют температурасына тура пропорционал болады.
(vmax / T) = b (b = 2,898*10-3)
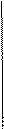
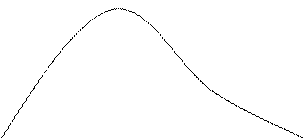

 E(T)
E(T)
λmax = b/T
λmax λ
26.Малюс жане Брюстер заны
Жарықты электромагниттік толқын ретінде сипаттайтын құбылыстардың бірі – жарықтың поляризациясы.
Поляризацияланған жарық деп Е жарық векторының тербелісі белгілі бір бағытта реттелген жарық толқынын айтады. Табиғи жарықта (Күннің жарығы, электр шамының жарығы және т.т.) жарық векторының тербелістері ортаның кез келген нүктесінде барлық мүмкін болатын бағыттарда, бірін-бірі тез, әрі бейберекет алмастырып отырып жасалады.
Егер Е векторының тербелістері сәуле арқылы өтетін тек бір жазықтықта жасалатын болса, онда толқын жазық поляризацияланған толқын болады. Е векторы тербеліс жасайтын жазықтық поляризация жазықтығы деп аталады.
Егер қандай да бір поляризациялық аспап жазық поляризацияланған сәулені алу үшін қолданылатын болса, онда ол поляризатор деп, ал егер осы аспап поляризацияланған сәулені зерттеу үшін пайдаланылса – анализатор деп аталады.
Поляризаторға интенсивтігі І0 жазық поляризацияланған сәуле түседі дейік; және поляризатордың өткізу жазықтығы түсетін сәуленің Е0 векторының тербеліс жазықтығымен α бұрыш жасайтын болсын. (1-сурет). Түсетін жазық поляризацияланған сәуледегі электрлік тербелістердің
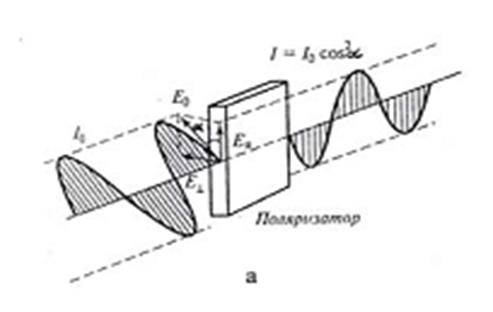
Е0 амплитудасын ЕІІ = E0 cosα және E┴ = E0 sinα екі құраушыға жіктейміз. Поляризатор арқылы бірінші тербеліс (ЕІІ ) өтеді, ал екінші тербеліс (E┴) өтпейді. Поляризаторға түсетін толқын интенсивтігі амплитуда квадратына пропорционал (І0 ~ Е02 ) болатындықтан, поляризатор арқылы өткен толқын интенсивтігі ЕІІ-тың квадратына пропорционал (І ~ ЕІІ2) болады, яғни
ЕІІ2 = E02 cos2α → I = I0 cos2α (1)
(1)қатысы Малюс заңы деп аталады, оны 1810ж. Француз физигі Э.Малюс тапқан.
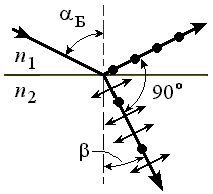
Диэлектриктердің бөлу шекарасындағы электромагниттік сәуленің поляризациялану процесінде шағылған және сынған сәулелердің поляризациялану дәрежесі табиғи сәуленің түсу бұрышына және диэлектриктердің сыну көрсеткіштерінің қатынасына тәуелді болады. Егер табиғи жарық сәулесі диэлектриктерді бөлу шекарасына қайсыбір α=αБ бұрышпен түсетін болса, онда оған сәйкес шағылған сәуле енді шала емес, толық поляризацияланған, яғни жазық поляризацияланған сәуле (ол тек Е┴ -толқын болады)болады. Ал сынған сәуле, осы жағдайда, шала поляризацияланған күйінде қалады(мұнда Е║-толқын басым болады),бірақ оның поляризациялану дәрежесі осы жағдайда барынша жоғары болады. αБ бұрышы мына шартты қанағаттандырады
tg αБ = n2 / n1 = n21 (2)
(2)өрнегін 1815ж. ағылшын физигі Д.Брюстер тапқан, ол Брюстер заңы, ал αБ – Брюстер бұрышы деп аталады.
27.Квантты-оптикалық құбылыстар.Фотоэлектрлік эффект.Комптон эффекті.
28.Фотондар.Фотон массасы және импульсі.
Фотон — электрмагниттік сәуленің (жарықтың) элементар бөлшегі. Фотон зарядсыз бейтарап (нейтрал) бөлшек. Ол вакуумде с=3×108м/с жылдамдықпен тарайды.
Фотонның массы мен импульсі. Эйнштейннің болжамы бойынша жарық фотондардың ағыны. Планктың болжамы бойынша жарықтың бір порциясының (квантының) энергиясы 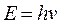 ; Екінші жағынан салыстырмалық теория бойынша энергия мен массаның арасында мынандай байланыс бар.
; Екінші жағынан салыстырмалық теория бойынша энергия мен массаның арасында мынандай байланыс бар. 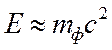 осыдан
осыдан 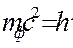
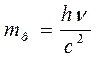
фотонның тыныштық күйдегі массасы нолге тең. Фотонның массасы мен жылдамдығы бойынша оның импульсін былай анықтаймыз. 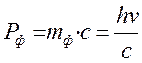
Фотонның импульсі жарық сәулесі мен бағыттас болады. Фотонның заряды және магнит моменті болмайды. Неғұрлым жиілігі көп болса , соғұрлым фотонның E мен P көп болады. Сөйтіп фотоэффект құбылысы жарықтың корпускулалық қасиеті бар екенін көрсетеді. Жалпы алған жарықтың екі жақты толқындық және корпускулалық қасиет болады.
Мысалы, фотон импульсі 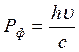 энергиясы
энергиясы 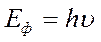 ұшып келіп электронмен соғыссын. Cоғысқаннан кейін
ұшып келіп электронмен соғыссын. Cоғысқаннан кейін 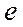 электрон фотоннан энергиясы мен импульсінің бөліктерін алып, қозғалысқа келеді. Электрон
электрон фотоннан энергиясы мен импульсінің бөліктерін алып, қозғалысқа келеді. Электрон 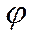 бағытында қозғалса, фотон
бағытында қозғалса, фотон 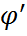 бағытында қозғалады.
бағытында қозғалады.
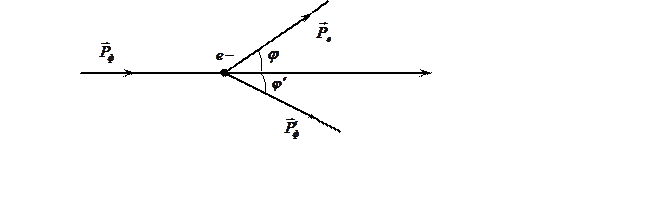
Фотонның энергиясы да, импульсі де азаяды, олай болса жиілігі де азаяды 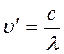 ; қатыста болғандықтан,
; қатыста болғандықтан, 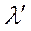 көбейе түседі.Рентген сәулелерінің жеңіл атомдармен соқтығысқан кезде, оның
көбейе түседі.Рентген сәулелерінің жеңіл атомдармен соқтығысқан кезде, оның 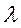 ұзаруын алғаш рет американ физигі Комптон ашты. (1923 ж). Бұл Комптон эффектісі деп аталады, толқын ұзындығы:
ұзаруын алғаш рет американ физигі Комптон ашты. (1923 ж). Бұл Комптон эффектісі деп аталады, толқын ұзындығы: 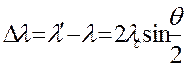
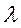 -түскен толқын ұзындығы,
-түскен толқын ұзындығы, 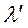 -шашыраған толқын ұзындығы.
-шашыраған толқын ұзындығы.
Фотон бос электрондарға тап болса, онда ол энергиясының біразы электрондарға береді де, өзінің қозғалыс бағытын өзгертеді, бұл Комптон эффектісі. Егер фотон атоммен байланысқан электронға кездессе, онда ол өз энергиясын түгелімен электронға береді. Энергия көбейген электрон металл бетіне бөлініп шығады, бұл фотоэлектрлік эффекті.
29.Бугер формуласын қорыту
Бугер заңы - жарықтың параллел монохроматты шоғының жұту қабілеті бар заттық ортада тарау барысында бiртiндеп әлсiретуiн анықтайтын заң.
Интенсивтігі І0 жарықтың параллель шоғы қалыңдығы мөлдір біртекті ортаның бетіне нормаль бағытталған болсын. Жұтылу нәтижесінде ортадан шыққан шоқтың интенсивтігі кемиді (оны І арқылы белгілейміз). Заттың берілген қабатында жұтылу заңдылығын анықтау керек.
Координаттар басын ортаның алдыңғы бетіне орналастырып, у осін осы бетке параллель бағыттаймыз, ал х осін – жарықтың таралу бағыты бойымен бағыттаймыз (1- сурет).
 y
y
 l
l
 |





 dx
dx




 I0 I
I0 I
 |  | ||||||
 | |||||||
 | |||||||

 x
x
Затта шексіз жіңішке қалыңдығы dx қабатты ойша бөліп аламыз. Қалыңдығы dx қабаттағы жарық интенсивтігінің кемуі осы қабатқа түсетін интенсивтіктің шамасына және жқтушы қабат қалыңдығына пропорционал, яғни
dI = - αIdx (1)
мұндағы α – жарық интенсивтігіне тәуелсіз, пропорционалдық коэффициент. Минус таңбасы жұтатын қабаттың қалыңдығы артқан сайын ол арқылы өтетін жарық интенсивтігінің кемитіндігін көрсетеді.
Қалыңдығы l қабаттан шығатын жарықтың интенсивтігі өрнегін алу үшін (1) өрнекті 0-ден l –ге дейінгі аралықта интегралдаймыз:
∫ dI / I = - ∫ αdx
Ортаның біртектілігіне және әрбір қабатта түсетін энергияның бірдей бөлігі жұтылатындығына байланысты ортаның жұтылу қабілетін сипаттаушы коэффициент, х координаттан да, интенсивтіктен де тәуелді болмайды. Демек, оны тұрақты ретінде интеграл астынан шығару,а болады. Сонда мынаны аламыз:
ln I – ln I0 = - αl
Осыдан
I = I0 e-αl (2)
мұндағы І0 және І – ортаның бетіне түсетін және қалыңдығы l қабаттан шығатын жарық интенсивтігі, α – жұтылу коэффициенті.
(2)формуланы 1729ж. Бугер тағайындап негіздеген, сондықтан Бугер заңы деп аталады.
Жұтылу коэффициентінің (α) сандық мәні l/ α мәніне тең d-қабаттың қалыңдығына сәйкес келеді және одан өткеннен кейін оның интенсивтілігі e=2,72 есеге азаяды. Бұл заңдылық заттағы жарық толқынының интенсивтілігі экспонента бойынша азаятынын көрсетеді. Егер жарық қалыңдығы d болатын материалдан өткен кезде оның интенсивтілігі N ретке азайса, қалыңдығы 2d болатын материалдан өткен кезде N2 ретке азаяды.

30.Фотоэффект үшін Эйнштейн теңдеуі.
Жарық әсер еткенде заттан электронның бөлініп шығу құбылысы фотоэффект деп аталады. Бұл құбылыс қатты денелерде, сұйықтықтарда, сондай-ақ газдарда да байқалады.
Ішкі фотоэффект (фотоөткізгіштік) кезінде жартылай өткізгіштер мен диэлектриктерге түскен жарық (фотон) оларда жұтылады да, сыртқа қарай электрондар бөлініп шықпайды. Сөйтіп, жартылай өткізгіштер мен диэлектриктердің электр өткізгіштігі өзгереді. Ішкі фотоэффектіні 1873 ж. америка физигі У.Смит байқаған.
Жарықтың әсерінен сұйықтардан және қатты денелерден электрондардың бөлініп шығу құбылысын сыртқы фотоэффект деп атайды.
Тәжірибе жүзінде сыртқы фотоэффектінің келесі заңдары ашылды:
1.Фотоэлектрондардың ең үлкен бастапқы жылдамдығы түскен жарықтың тербеліс жиілігімен анықталады, жарықтың интенсивтілігіне тәуелді болмайды.
2.Барлық заттар үшін фотоэффектінің қызыл шекарасы болады. Сыртқы фотоэффект байқалатын ең үлкен толқын ұзындығын (ең кіші тербеліс жиілігін) фотоэффектінің қызыл шекарасы деп атайды.
3.Катодтан бірдік уақытта ұшып шығатын фотоэлектрондардың саны жарықтың интенсивтілігіне тура пропорционал.
Энергияның сақталу заңын қолдана отырып Эйнштейн фотоэффект заңын алды.
Фотоэффект құбылысы кезінде фотонның энергиясының бір бөлігі шығу жұмысына жұмсалады,ал қалған бөлігі денеден бөлініп шыққан электронның кинетакалық энергиясын арттыруға жұмасалады.
Сыртқы фотоэффект үшін Эйнштейн формуласы:
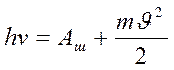
Жарық бөлшегін – фотон деп атайды. Фотон энергиясы оның тербеліс жиілігімен анықталады.
ε = hv немесе ε = ћω
Фотон импульсі: P = ε/c = hv/c = h/λ
Фотонның массасы келесі формуламен анықталады:
m = ε/c2 = hv/c2 = h/cλ
Тыныштық күйдегі фотон массасы нольге тең.








