Когерентті толқын — егер екі толқынның тербеліс жиілігі мен тұрақты фаза ығысуы бірдей болса, олар когерентті толқындар деп аталады.

Дата: 2025-06-02; Просмотры: 9
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

1. Фотометриялық ұғымдар мен шамалар, олардың өлшем бірліктері

Жарық толқыны энергия тасымалдайды. Əртүрлі оптикалық зерттеулерді жүргізгенде жарық энергиясын жəне онымен байланысты шамаларды өлшеу қажет болады. Оптикалық аумаққа жататын электромагниттік толқындардың тасымалдайтын энергиясын өлшеулермен шұғылданатын оптика бөлімі фотометрия деп аталады.

Фотометриялық шамаларда негізгі шама ретінде жарық күші алынады. Жарық күшінің бірлігі – кандела қара сәуле шығарғыш көмегімен анықталады. Жарық күші dIV арқылы белгіленеді.

Жарық ағыны. Жарық ағыны деп жарық көзінің dIV жарық күшінің, ішінде шығарылған жарық таралатын dΩ денелік бұрышқа көбейтіндісін айтады.

dФV = dIV * dΩ

Жарық ағынының спектрлік тығыздығы мына формуламен анықталады:

dФVλ = dIVλ * dΩ

Жарықтылық. Жарықтылық BV арқылы белгіленеді.

BV = dIV / dσ`

BVλ = dФVλ / dΩdσcosθ

Жарықтылықтың өлшем бірлігі—в аттың стерадиан-метр квадратқа қатынасы Вт/(ср-м2).

Жарқырау. Жарқырау RV арқылы белгіленеді.

RV = dФV / dσ

Жарқыраудың өлшем бірлігі – (Вт/м2).

Жарықталу. Жарықталу мен жарықталудың спектрлік тығыздығы мына қатынастармен анықталады:

EV = dФV / dσ

EVλ = dФVλ / dσ

Жарықталынудың өлшем бірлігі— ватт бөлінген метр квадрат (Вт/м2).

Жарық экспозициясы. Бұл шама мына формуламен анықталады

dHV = ФVdt

мұндағы dt – уақыт аралығы, осы уақыт аралығы ішінде ФV жарық ағыны шығарылады немесе қабылданады.

 

2. Айна. Сфералық айна және линзалар

Айна, оптикалық — беті тегіс, жарық сәулесін шағылдыратын, нәрсенің оптикалық кескінін беретін шыны немесе металл дене.

Айнадан жарық сәулесі түсу және шағылу бұрышының тепе-теңдігін сақтай отырып шағылады. Ең көп тараған түрі — оптикалық жазық айна. Сондай-ақ оптикалық жүйелерде сфералық, параболалық, эллипсоидтық т.б. шағылдырғыш беттері бар дөңес және ойыс айналар да қолданылады.

Сфералық айналар шар тектес беттің бір бөлігі, және дөңес, ойыс болып бөлінеді.

 

 

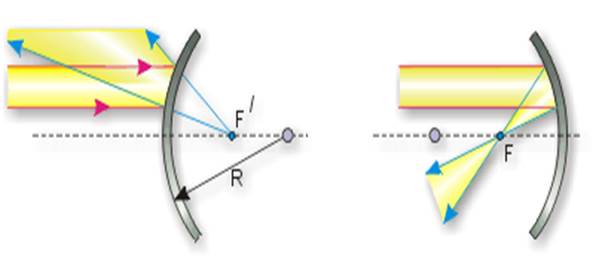
Дөңес айнаға параллель жарық шоқтарын түсірейік. Олар айнадан шағылып шашырайды. Сондықтан да дөңес айналарды шашыратқыш деп атайды. Ал ойыс айнаға сол параллель жарық шоқтарын түсірсек, олар бас фокуста жиналады. Осы қасиеті үшін ойыс айналар жинағыш болып аталады. Бұл жердегі F және F` бас фокустары деп аталады. Дөңес айнада ол жорамал, өйткені жарық фокустан өтпейді, ал ойыс айнада ол шын.

 

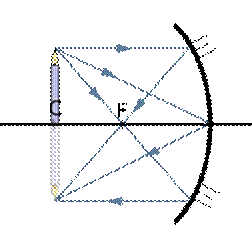Фокусты табу үшін қисықтық радиусын білу керек, сонда келесі формулаға келеміз: F=R/2. Бұл формула дөңес және ойыс айнаға да орындалады.Дөңес айна

үшін келесі формула орындалады: 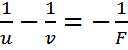бұл жердегі F = ал u-зат пен айна,

v-бейне мен айна арақашықтығы.Ал ойыс сфералықайналар үшін

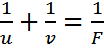
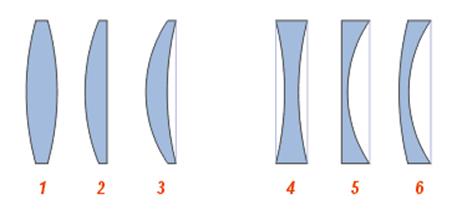
Линза дегеніміз - екі жақы сфералық беттермен

шектелген мөлдір дене. Олар шашыратқыш және жинағыш болып келеді. Жинағыш және шашыратқыш линзаларды сипаттайтын негізгі параметрлер ретінде келесі параметрлерді көрсетсек болады:

 

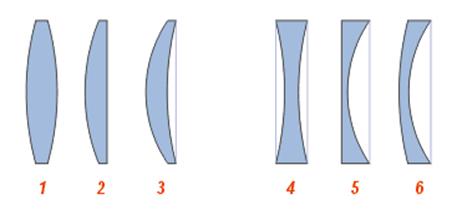
1) Линзаның оптикалық центрі, ол линзаның дәл центрінде орналасады.

2) Линзаның оптикалық осьі, ол оптикалық центрден өтіп, линзаның қырларына перпендикуляр болады.

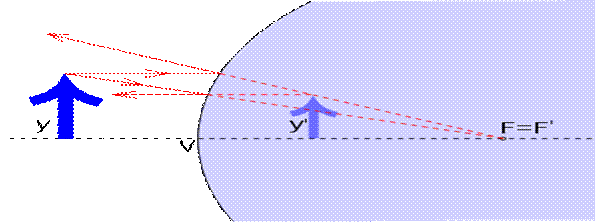
3) Линзаның фокустық арақашықтығы, линзаға қандайда бір параллель жарық шоқтарын түсірген кезде олардың қиылысқан жері фокустық арақашықтығы болады. Ойыс линзада ол жорамал, ал дөңес линзада шын. Дөңес линза үшін F>0, ойыс линзаға F<0.

4) Линзаның оптикалық күші. Фокустық арақашықтыққа кері пропорционал D=1/F. Өлшем бірлігі диоптрия (дптр). Жинақтағыш немесе дөңес линза үшін D>0 , ал шашыратқыш ойыс линза үшін D<0.

5) Линза жасалған оптикалық материалдың сыну көрсеткіші. Жоғарыда айтылғанның барлығы линзаның сыну көрсеткіші ол орналасқан ортаның сыну көрсеткішінен көп болса ғана орындалады.

 

 

3. Геометрилық оптиканың негізгі заңдары

Геометриялық оптика заңдары жарықтың физикалық табиғаты анықталғаннан әлдеқайда бұрын белгілі болатын.

1. Жарықтың түзусызықты таралу заңы: оптикалық тығыздығы біртекті ортада жарық түзусызықты таралады. Бірақ жарық сәулесі өлшемдері жарықтың толқын ұзындығына шамалас болатын кедергілерден өткен кезде жарық түзусызықты таралу заңынан ауытқиды және жарық сәулесі деген ұғымды қолдануға болмайды. Екі мөлдір ортаның шекарасында жарықтың бір бөлігі шағылуы мүмкін және ол шағылғаннан кейін жаңа бағытпен таралады, ал басқа бөлігі шекарадан өтіп екінші ортада таралуы мүмкін.

2. Жарықтың шағылу заңы: түскен және шағылған сәуле және сәуленің түскен нүктесінде екі ортаның шекарасына тұрғызылған перпендикуляр бір жазықтықта жатады (түсу жазықтығы). g шағылу бұрышы a түсу бұрышына тең болады.

3. Жарықтың сыну заңы: түскен және сынған сәуле және сәуленің түскен нүктесінде екі ортаның шекарасына тұрғызылған перпендикуляр бір жазықтықта жатады. a түсу бұрышы синусының b сыну бұрышы синусына қатынасы берілген екі орта үшін тұрақты шама болады:

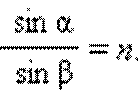(1)

Сыну заңы Голландия ғалымы В. Снеллиус (1621 ж.) тәжірибе жүзінде тағайындаған.

 

n 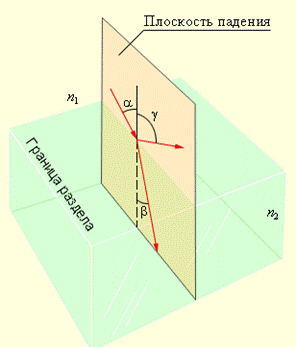тұрақты шама екінші ортаның бірінші ортаға қарағандағы салыстырмалы сыну көрсеткіші деп аталады. Екі ортаның салыстырмалы сыну көрсеткіші олардың абсолют сыну көрсеткіштерінің қатынасына тең:

n = n2 / n1 (2)

1 сур. жарықтың шағылу және сыну заңдары бейнеленген. Абсолют сыну көрсеткіші аз ортаны оптикалық тығыздығы аз орта деп атайды. Шағылған және сынған сәулелердің энергия мөлшері сыну коэффициенті мен түсу бұрышына тәуелді болады.

Шағылу және сыну заңдары:

g = a; n1 sin a = n2 sin b.

4. Жарық тәуелсіздігі: яғни бір жарық басқа жарыққа кедергі жасай алмайды, және бір жарық бөлшектері басқа бөлшектерсіз тарала алады. Мысалға жарық жолына мөлдір емес экран қойсақ ол бір бөлігін бөліп алып қалса, қалған бөлігі тәуелсіз еш өзгеріссіз бағытымен тарала береді.

5. Жарықтың қайтымдылығы. Яғни қандай да бір ортадан басқа бір ортаға бір жол жүріп жетсе, соңғы нүктеде ол тура шағылса, ол тура сол жолмен жарық көзіне қайтып келеді.

 

4. Толық ішкі шағылу құбылысы

Жарық оптикаша тығыздығы артық ортадан оптикаша тығыздығы кем ортаға (абсолют сыну көрсеткіші аз) таралғанда, түсу бұрышының ұлғаюына байланысты, шағылған жарық энергиясының бөліктері де өседі. Бірақ та түсу бұрышының кейбір мәнінен бастап сәуленің барлық жарық энергиясы шекаралық беттен шағылады да жарық бірінші ортадан екінші ортаға өтпейді (толық ішкі шағылу құбылысы). Түскен жарық түгел шағылып, кейін серпіледі. Яғни сыну бұрышы белгілі бір градусқа тең болғандағы бұрыш 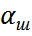деп аталады, 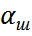- толық ішкі шағылу бұрышы. 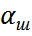және одан үлкен бұрыштарда толық ішкі шағылу құбылысы байқалады. Яғни жарық тек шағылады, ал сыну бұрышы шекараға паралелль немесе мүлдем жоқ болады.

 

5. Жазық және сфералық айналардан кескін алу

 

 

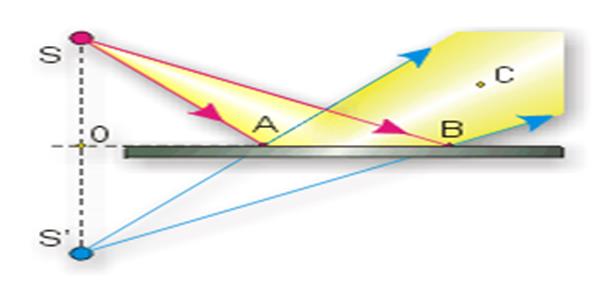
Жазық айнаға S жарық көзінен жарық түссін. Жазық айнаға түскен SA SB жарық шоқтары суретте көрсетілгендей бағытта шағылады. Суреттегідей С нүктесінде бақылаушы тұрса, ол айнаның артында тұрған S` жарық көзін көреді. Суреттен байқалатындай SO S`O өзара тең, және SS` айнаға перпендикуляр. Сонымен жазық айнадағы бейнелер жорамал болып келеді. Өйткені ол бейнелер жарық жоқ жерлерден шығады. Бейне айнадан және зат айнадан бірдей арақашықтықта орналасады.

 

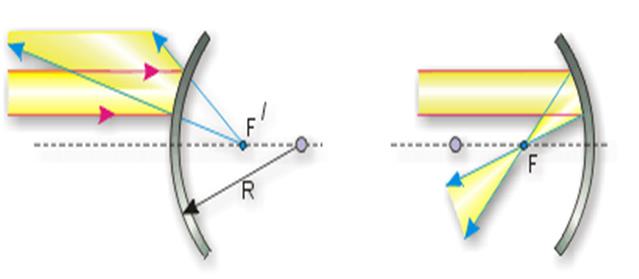
Жазық айналардан бөлек сфералық айналар болады. Олар шар тектес беттің бір бөлігі, және дөңес, ойыс болып бөлінеді. Дөңес айнаға параллель жарық шоқтарын түсірейік. Олар айнадан шағылып шашырайды. Сондықтан да дөңес айналарды шашыратқыш деп атайды. Ал ойыс айнаға сол параллель жарық шоқтарын түсірсек, олар бас фокуста жиналады. Осы қасиеті үшін ойыс айналар жинағыш болып аталады. Бұл жердегі F және F` бас фокустары деп аталады. Дөңес айнада ол жорамал, өйткені жарық фокустан өтпейді, ал ойыс айнада ол шын.

 

 

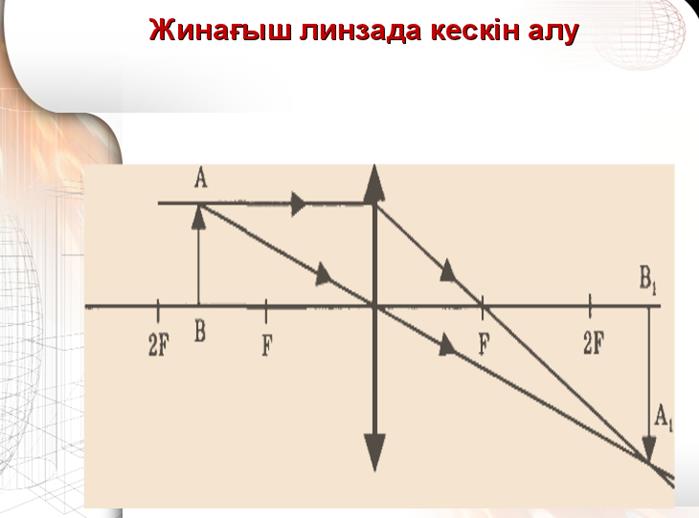
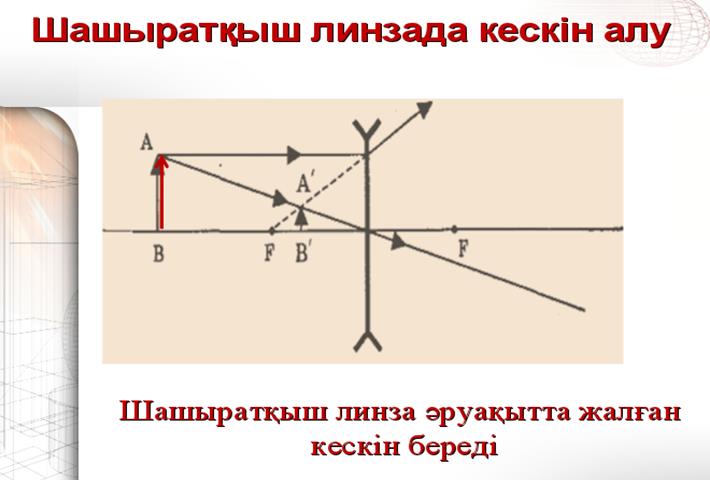
6. Жинағыш және шашыратқыш линзалар. Кескін алу.

Линза дегеніміз - екі жақы сфералық беттермен

шектелген мөлдір дене. Олар шашыратқыш және жинағыш болып келеді. Жинағыш және шашыратқыш линзаларды сипаттайтын негізгі параметрлер ретінде келесі параметрлерді көрсетсек болады:

 

6) Линзаның оптикалық центрі, ол линзаның дәл центрінде орналасады.

7) Линзаның оптикалық осьі, ол оптикалық центрден өтіп, линзаның қырларына перпендикуляр болады.

8) Линзаның фокустық арақашықтығы, линзаға қандайда бір параллель жарық шоқтарын түсірген кезде олардың қиылысқан жері фокустық арақашықтығы болады. Ойыс линзада ол жорамал, ал дөңес линзада шын. Дөңес линза үшін F>0, ойыс линзаға F<0.

9) Линзаның оптикалық күші. Фокустық арақашықтыққа кері пропорционал D=1/F. Өлшем бірлігі диоптрия (дптр). Жинақтағыш немесе дөңес линза үшін D>0 , ал шашыратқыш ойыс линза үшін D<0.

10) Линза жасалған оптикалық материалдың сыну көрсеткіші. Жоғарыда айтылғанның барлығы линзаның сыну көрсеткіші ол орналасқан ортаның сыну көрсеткішінен көп болса ғана орындалады.

 

 

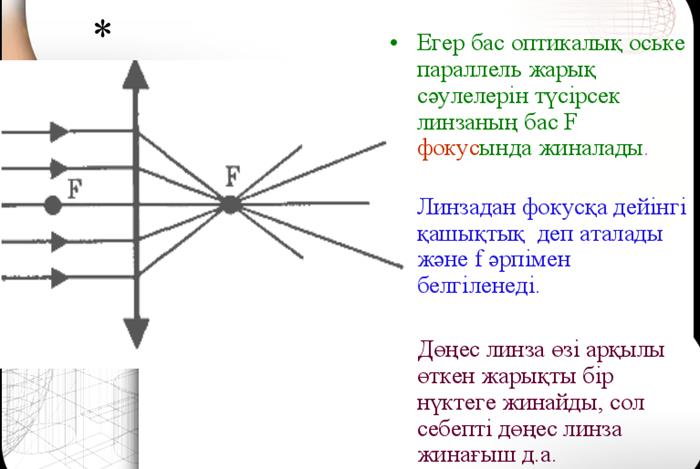
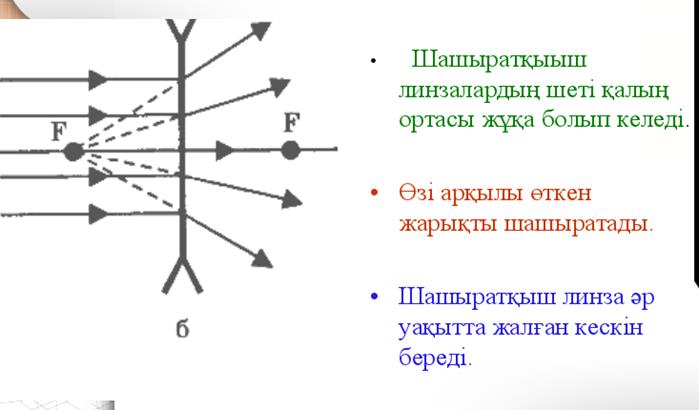
7. Линзаның бас фокус аралығы және оптикалық күші. Жұқа линза теңдеуі

Линзаға қандайда бір параллель жарық шоқтарын түсірген кезде олардың қиылысқан жері фокустық арақашықтығы болады. Ойыс линзада ол жорамал, ал дөңес линзада шын. Дөңес линза үшін F>0, ойыс линзаға F<0.

Фокустық арақашықтыққа кері пропорционал D=1/F. Өлшем бірлігі диоптрия (дптр). Жинақтағыш немесе дөңес линза үшін D>0 , ал шашыратқыш ойыс линза үшін D<0.

Жұқа линза: қалыңдығы d линзаның R қисықтық радиусынан көп кіші линза.

d << R

 

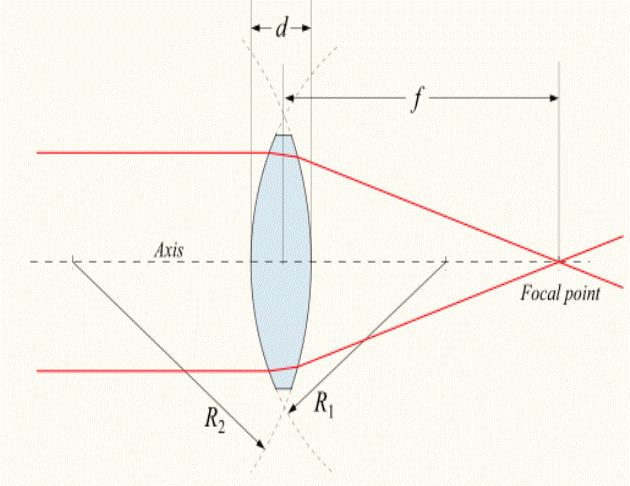
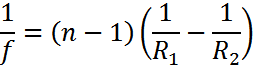
d - линза қалыңдығы; 𝑓- фокус аралығы; n - сыну көрсеткіші; R1, R2 - линза бетінің қисықтық радиусы

 

8. Жарық толқынының интерференциясы

Жарық табиғаты жайлы екі теория қалыптасқан: корпускулярлық және толқындық. Жарықтың толқындық теориясы Гюйгенс принципіне негізделген: толқын келіп жеткен кез-келген нүкте екінші реттік толқын көзі болып табылады, ал осы толқындарды шектеуші сызық келесі уақыт мезетіндегі толқындық майдан орнын береді. Толқындық майдан деп 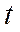уақыт мезетінде тербелістер келіп жететін нүктелердің геометриялық орнын айтады.Интерференция құбылысын толқынның интерференциясын мысалға ала отырып түсіндіруге болады. Жарық интерференциясы үшін қажетті шарт: жарық толқындары монохроматты және когерентті болуы қажет. Интерференция құбылысын бақылау үшін, бір жарық көзінің сәулесін екі саңылаудан өткізіп, оларды когерентті жарық көздері ретінде қарастырады . 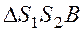және 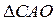үшбұрыштарынан 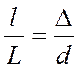, одан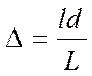

мұнда 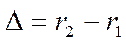- толқындар жүрісінің айырмасы; 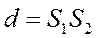; 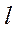- экран ортасынан интерференция бақыланатын А нүктесіне дейінгі қашық.

 

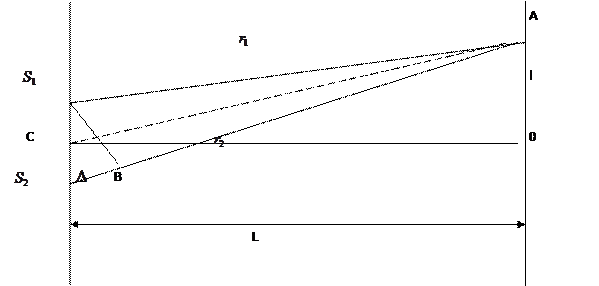
Толқындар жүрісінің айырмасы 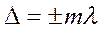, 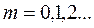болғанда интерференциялық максимум, ал , 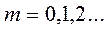болғанда интерференциялық минимум бақыланады.

А нүктесіндегі максимум ;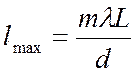

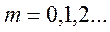
ал минимум ;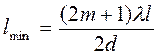

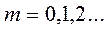
Көршілес екі максимумдар (немесе) минимумдардың арақашықтығы интерференциялық жолақтың ені делінеді

 

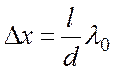
9. Тербелістер мен толқындардың когеренттігі және интерференцияcы

Егер тербеліс фазаларының айырмасы уақыт бойынша тұрақты әрі ол қосынды тербелістің амплитудасын анықтайтын болса, онда мұндай тербелістер когерентті тербелістер деп аталады (мысалы, жарық толқындарының Когеренттігі).

Бірдей жиіліктегі екі гармониялық (синусоидалық) тербеліс әрқашан когерентті болады. Когеренттік электрмагниттік толқындарда да байқалады. Когерентті толқындар қосылған кезде бір-бірін күшейтеді не әлсіретеді (толқын интерференциясы байқалады).

Когерентті толқын — егер екі толқынның тербеліс жиілігі мен тұрақты фаза ығысуы бірдей болса, олар когерентті толқындар деп аталады.

Когерентті жарық толқындары қабаттасқанда интерференциялану құбылысы байқалады. Өзара перпендикуляр жазықтықтарда полярланған жарық толқындары интерференцияланбайды. Ондай толқындарды интерференциялау үшін олардың тербелістерін бір жазықтыққа келтіру керек.

Кеңістікте бір немесе бірнеше когерентті толқындар қабаттасқанда оның бір нүктелерінде тербелістер күшейеді, келесі бір нүктелерінде әлсірейді. Осы құбылысты интерференция дейді.

Егер тербеліс көздері бірдей жиілікпен, бірдей бағытта, бірдей фазада не тұрақты фазалар айырмасында тербеліс жасаса, ондай көздерді когерентті тербеліс көздері деп атайды.

Екі нүктелік тербеліс көздерінен шығатын сфералық когерентті толқындардың қосылуын қарастырайық .

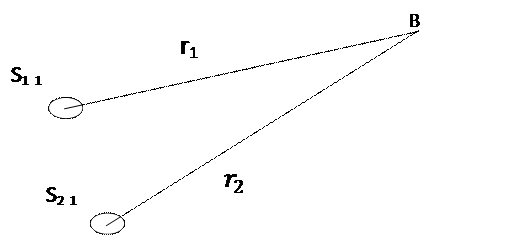
Толқындардың тербеліс ампитудалары , жиіліктері 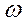және фазаларының айырмасы тұрақты болсын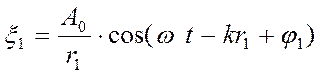

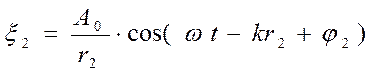
мұндағы 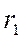және 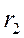тербеліс көздерінен 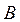нүктесінің

қашықтығы; 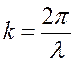толқындық сан; 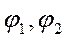– қабаттасатын толқындардың алғашқы фазалары.

В нүктесіндегі қорытқы толқын амплитудасы

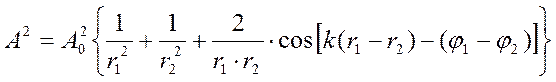
Алғашқы фазалар айырмасы тұрақты болғандықтан 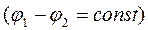қорытқы тербеліс амплитудасы толқындар жүрісінің айырмасына байланысты болады. Фазалар айырмасы

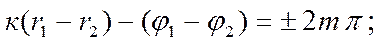
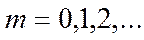
болатын нүктелерде интерференциялық максимум байқалады. Қорытқы тербеліс амплитудасы

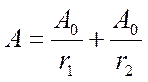Фазалар айырмасы:

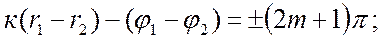
болатын нүктелерде интерференциялық минимум байқалады. Қорытқы тербеліс амплитудасы

 

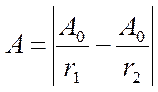
10. Интерференциялық жолақтардың ені

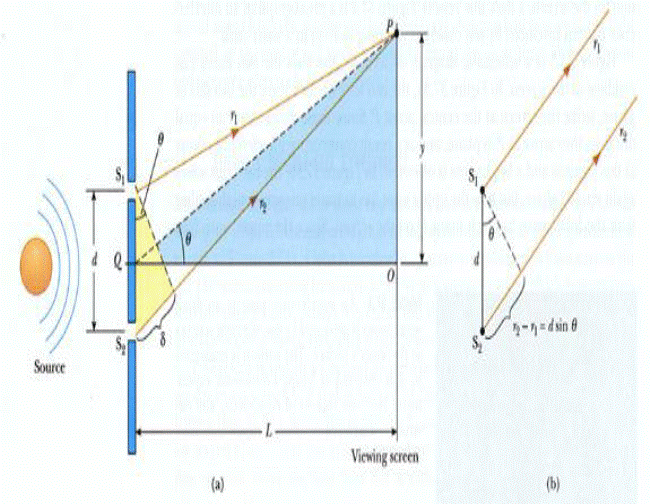
Юнг әдісі. Жарықтың интерференция құбылысын бірінші бақылаған және түсіндірген – Юнг. Юнг тәжірибесінде жарық көзі жарықтандырылған S саңылауы бұдан шыққан жарық толқынының әртүрлі бөліктері жіңішке саңылауларына түсіп, оларды жарықтандырады. Жарық кіші саңылаулардан өтіп , дифракция әсерінен, нәтижесінде бастапқы бағытынан ауытқиды. Сондықтан толқынның 2 бөлігі қабаттасады да интерференция құбылысы пайда болады. Юнг тәжірибесінде интерференцияны бақылау үшін саңылаулар ені өте кішкене болуы тиіс. жарық көздері мен экран орналасқан ортаның сыну көрсеткіші n болса, онда жарық толқындарының оптикалық жол айырымы: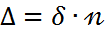

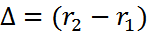n=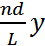

P нүктесіндегі жарықталудың максимумдық шарты 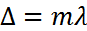, мұндағы (m=0,1,2,..)

P нүктесіндегі жарықталудың минимумдық шарты 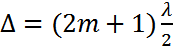, мұндағы (m=0,1,2,..)

Максимум және минимум координаталарының анықталуы

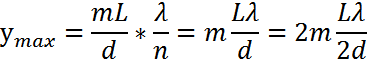
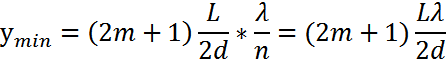
Көршілес 2 максимум немесе минимумдардың арақашықтығы 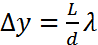. Интерференциялық жолақтардың ені осы формуламен анықталады.

 

11. Интерференциялық аспаптар. Ньютон сақиналары.

Интерферометрлер - жарықтың интерференция құбылысы мөлдір орталардың сынукөрсеткіштерін, спектрлік сызықтардың толқын ұзындықтарын, бұрыштарды және т.т. дәл өлшеулер үшінқолданылатын оптикалық құрылғылар. Интерферометрдің өлшеу дәлдігін арттыру үшін жүріс айырымын едәуір өсіру керек болады. Осындай жағдайларда сәуленің жоғары монохроматтығы және оптикалық жүйенің юстировкасына аса жоғары талаптар қажет.Барлық белгілі интерференциялық аспаптарды негізінен екі топқа бөлуге болады: екісәулелік және көп сәулелік.

Майкельсон интерферометрі.Бұл интерферометр ғылым мен техниканың дамуында іргелі роль атқарды. Оның көмегімен жарық толқынының ұзындығы алғаш өлшенді, спектрлік сызықтардың нәзік түзілісіне бірінші жүйелі зерттеулер жүргізілді, спектрлік сызықтардың толқын ұзындықтарын эталондық метрмен тікелей салыстыру бірінші орындалды.

Ньютон сақиналары:Егер жұқа пластинканың беттері бір-біріне параллель болмаса, онда бұларды аумақты жарық көзімен жарықтандырған кезде тұрақты оптикалық қалыңдық жолақтары, немесе бірдей қалыңдықжолақтары пайда болады. Бірдей қалыңдық жолақтарын қалқаға (экранға) пластина бетінің кескіні проекцияланған жағдайда бақылауға болады.Егер пластинка сына пішіндес болса, онда бірдей қалыңдық жолақтар сына қырына параллель интерференциялық жолақтар қатары түрінде болады. Пленканың осындай пішінін тік орналастырылған сым шеңберге керілген сабын пленкасы (қабыршығы) көмегімен алуға болады.

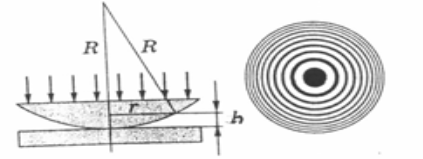
Ньютон сақиналары қисықтығы аз линзаның дөңес беті шыны пластинаның жазық бетімен қайсыбір

1-сурет

 

нүктеде түйіскен жағдайда, бұлардың араларындағы түйісу нүктесінен шеттеріне қарай біртіндеп өсетін, сына пішіндес ауа қабатында пайда болады (1-сурет). Линзаға монохроматты жарық ағыны тік түсетін болсын. Сонда жарық толқындарының ауа қабатының үстіңгі және астыңғы шекараларынан шағылуы нәтижесінде интерференция байқалады. Шағылған жарықта бақылағанда түйісу нүктесінде қараңғы дақ болады да, ал оны ені кеміп отыратын жарық және қараңғы концентрлік сақиналар жүйесі қоршап тұрады. Орталық қараңғы дақ геометриялық жүріс айырымы нөлге тең болатындықтан және жазық шыны пластина бетінен шағылған кезде жарты толқынның жоғалуы нәтижесінде пайда болады.

Ауа қабатының m -і сақинаға сәйкес келетін 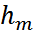қалыңдығы осы сақинаның 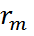радиусы және линзаның R қисықтық радиусымен мына қатынаспен байланысқан: 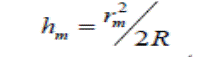(1) 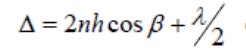формуладағы

cosβ =1 (жарық тік түседі) және n =1 (линза мен пластинка арасында ауа) деп алып, m -і қараңғы сақинаның түзілу шартын табамыз 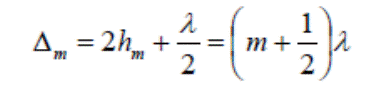(2)

(2) формулаға 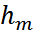мәнін қойып, сақина (шеңбер) радиусы үшін өрнекті аламыз: 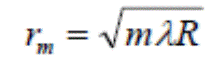(3)

(3) формуладан m = 0 және 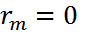болғанда, яғни центрде, қараңғы дақ болатындығы келіп шығады. Интерференция реті неғұрлым үлкен болса, сақиналар жиірек орналасатын болады.

 

12.Жарық толқынының дифракциясы.

Жарықтың дифракциясы деп жарық

толқындарының жолында кездесетін бөгеттерді айналып өтуін айтады. Жарықтың дифракциясы байқалуы үшін жарық жолындағы бөгеттердің өлшемдері жарықтың толқын ұзындығымен шамалас болуы ( 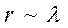) керек. Жарық дифракциясының бiр мысалы оның тар жолақ саңлау арқылы өткен кездегi дифракциясы. Дифракцияның екі түрі кездеседі:1.Тоғысатын немесе шашырайтын сәулелер дифракциясы, яғни Френель дифракциясы; 2.Параллель сәулелер дифракциясы, яғни Фраунгофер дифракциясы.

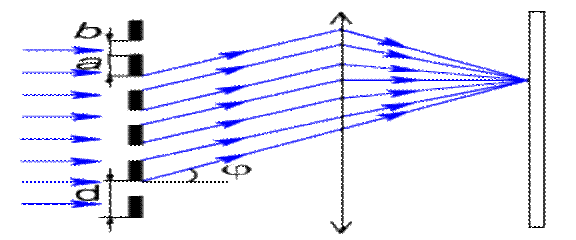
Дифракциялық тордың суреті (a - күңгiрт жолақтың енi, b – саңлаудың енi)

Айталық торға жарық перпендикуляр бағытта түсірілген болсын. Саңылаудың артында дифракция нәтижесінде сәулелер торға түскен сәулелерге қандай да бір бұрыш жасай отырып, таралатын болады. Егер осы сәулелердің жолына жинағыш линзаны орналастыратын болсақ, осы линзаның фокальдық жазықтығында бір нүктеде бірдей бұрышпен ауытқыған сәулелер жинақталады. Бір- біріне сәйкес сәулелердің арасындағы оптикалық жол айырымы 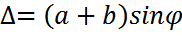тең болады, мұнда 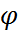– саңылауға түсетін сәуле мен ауытқыған сәуле арасындағы бұрыш, немесе 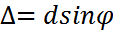, мұнда d =a+b – дифракциялық тордың периоды, осы жол айырымына сәйкес келетін фазалар ;

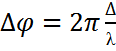Егер 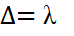болса, онда 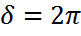, демек сәулелер бір фазада жетеді және бірін-бірі күшейтеді. Осы жағдай үшін максимумдардың болу шарты: 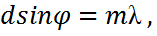мұнда m = 0; 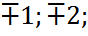. Осы максимумдар негізгі деп аталады. Максимумдар шартынан m=0 болса, 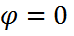және экранда нөлінші ретті максимум алынады. m= 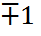болса, нөлінші реттің екі жағында да екі бірінші ретті максимумдар пайда болады және т.с.с.

Дифракциялық торды ақ жарықпен жарықтандырса, ақ жарықтың нөлінші ретті жолағы пайда болады, өйткені 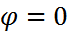үшін максимум шарты кез келген толқын ұзындықтары үшін орындалады. m 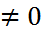ретті әр жолақ спектр болады, сонымен бірге қызыл шетіне дифракцияның үлкен бұрышы сәйкес келеді.

Максимумдар екпінділігі біртіндеп азая бастайды, дифракциялық спектрдің саны шектеулі және ол мына шарт бойынша анықталады.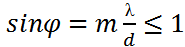

 

13.Дифракция құбылысы. Гюйгенс-Френель принципі.

Жарық толқындары оптикалық біртексіз ортада таралғанда байқалатын және геометриялық оптиканың заңдылықтарынан ауытқумен жүретін құбылыстардың жиынтығын дифракция деп атайды. Жеке жағдайда жарықтың дифракциясы деп жарық толқындарының жолында кездесетін бөгеттерді айналып өтуін айтады. Жарықтың дифракциясы байқалуы үшін жарық жолындағы бөгеттердің өлшемдері жарықтың толқын ұзындығымен шамалас болуы ( 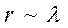) керек. Дифракция құбылысы жарықтың толқындық қасиетiнiң айқын дәлелi болып табылады. Бұл құбылыс геометриялық оптика заңдылықтарының қай кезде бұзылатындығына нұсқайды. Дифракцияның екі түрі кездеседі:1.Тоғысатын немесе шашырайтын сәулелер дифракциясы, яғни Френель дифракциясы; 2.Параллель сәулелер дифракциясы, яғни Фраунгофер дифракциясы.

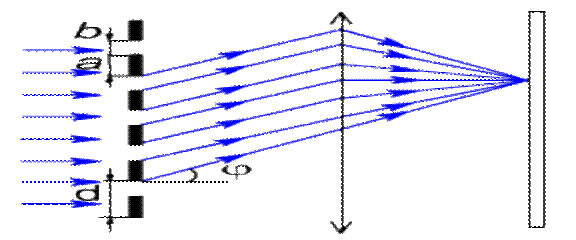
Дифракциялық тордың суреті (a - күңгiрт жолақтың енi, b – саңлаудың енi).

Жарықтың жолында кездескен бөгеттерді айналып өтуін Гюйгенс принципімен түсіндіруге болады. Гюйгенс принципі бойынша кеңістіктің толқын жеткен кез-келген нүктесін екінші реттік толқын көзі деп қарастыруға болады. Француз ғалымы Френель Гюйгенс принципін екінші реттік толқынның амплитудасын және интенсивтілігін ескеріп, толықтырды.Френель-Гюйгенс принципі:Кеңістіктің толқын жеткен нүктелері тек қана екінші реттік толқын көздері болып табылмай және олардың интерференциясының нәтижесі болып табылады.

1. Жарық толқындары келiп жеткен беттiң әрбiр нүктесi өз кезегiнде жаңа толқын көздерi болып табылады. 2. Бұл жаңа толқын көздерi бiр-бiрiне когеренттi. Ал кеңiстiктiң кез-келген нүктесiндегi жарықтың интенсивтiлiгi осы когеренттi жаңа көздерден тараған толқындардың интерференциясының салдары болып табылады.

Гюйгенс-Френель принципi дифракциялық бейнелермен қатар жарықтың түзу сызық бойымен таралу себебiн де түсiндiредi.

 

14.Френель және Фраунгофер дифракциясы

Жарықтың дифракциясы деп жарық

толқындарының жолында кездесетін бөгеттерді айналып өтуін айтады. Дифракцияның екі түрі кездеседі:1.Тоғысатын немесе шашырайтын сәулелер дифракциясы, яғни Френель дифракциясы; 2.Параллель сәулелер дифракциясы, яғни Фраунгофер дифракциясы.