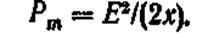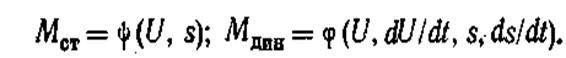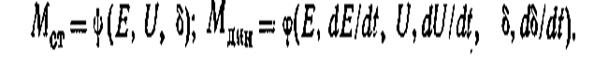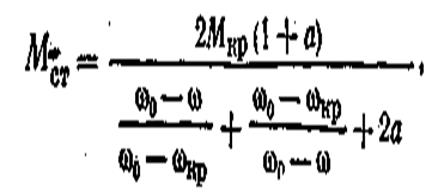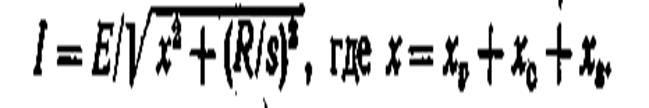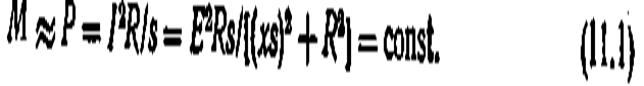32 Статическая устойчивость узлов комплексной нагрузки. Критерии устойчивости комплексной нагрузки.

Дата: 2025-06-15; Просмотры: 6

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Комплексная нагрузка состоит из осветительной, бытовой нагрузки, нагрузок двигателей инверторов и выпрямителей, а также потерь в трансформаторах и кабелях. Её динамические характеристики могут приближенно получены из серии статических характеристик.

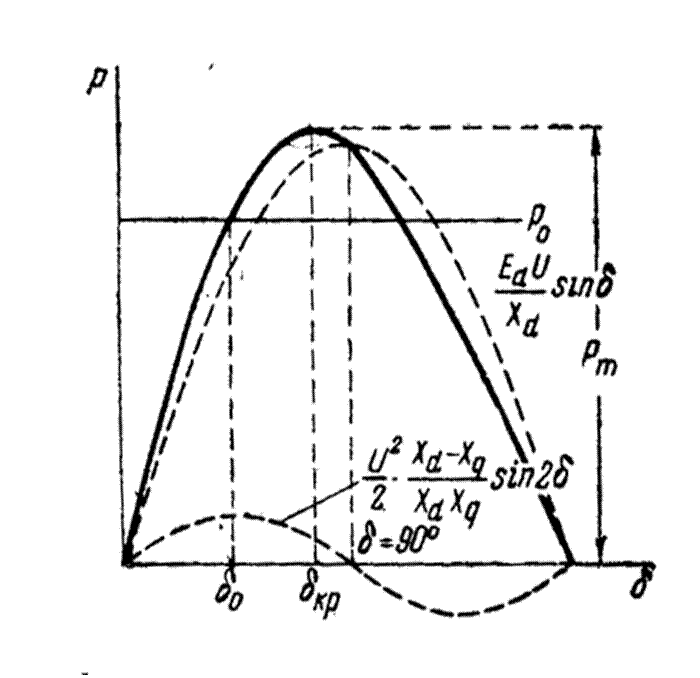
Изменения мощности, потребляемой нагрузки, с изменением напряжения и частоты могут быть при небольших медленных и быстрых изменениях представлены выражениями:

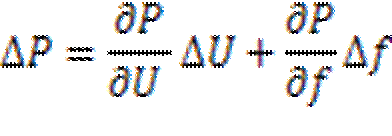
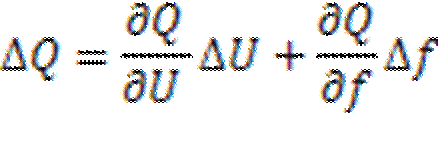
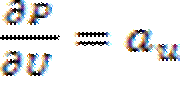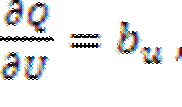
Величины , , 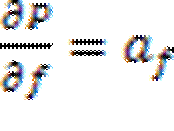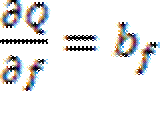- регулирующие эффекты активной и реактивной мощностей нагрузки по напряжению и частоте, взятые от статических и динамических характеристик соответственно.

Регулирующий эффект комплексной нагрузки при медленном изменении (статическая характеристика) напряжения вблизи его нормального значения составляет 1.5 – 3.5 для реактивной мощности и 0.3 – 0.5 для активной мощности.

Регулирующий эффект комплексной нагрузки при изменении частоты вблизи её норм. значения составляет 1.5 – 3 для активной мощности и 1 – 6 для реактивной.

Величины регулирующего эффекта при быстрых изменениях меняется в зависимости от скорости изменения напряжения и частоты. Обычно диапазон регулирующего эффекта для отдельных слагающих нагрузки больше, чем для всей комплексной нагрузки.

Нагрузка замещается сопротивлением:

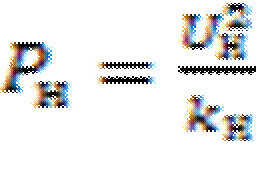
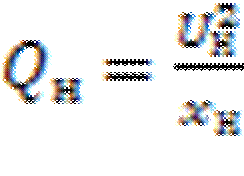
33 Большие возмущения в узлах системы электроснабжения. Уравнение движения агрегата “двигатель-механизм”

Большое возмущение – это возмущение, влияние которого на характер поведения системы существенно зависти от времени существования, значения и места появления возмущающегося воздействия, в связи с чем система во всем диапазоне исследования должна рассматриваться как нелинейная.

К большим возмущениям относятся:

· одновременный пуск значительного количества ЭД, АПВ, АВР;

· самозапуск ЭД;

· мощные толчкообразные нагрузки

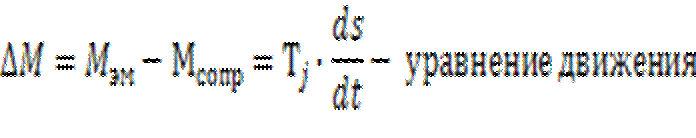
34 Статическая устойчивость СД. Угловая характеристика мощности СД. Критерии устойчивости СД.

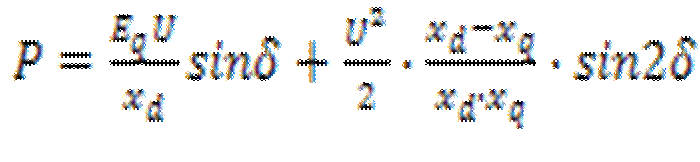- Угловая характеристика, в уравнение которой входит не только основная синусоидальная составляющая 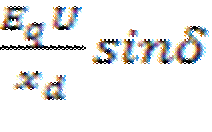а также и вторая составляющая в виде синусоиды двойной частоты, амплитуда которой пропорциональна разности реактансов в продольной и в поперечной осях , и не зависти от ЭДС. Она немного смещает максимум характеристики мощности и критический угол, при котором достигается максимум мощности, получается меньше 90. Это не влияет на ухудшение устойчивости, потому что одновременно уменьшается начальный угол δо при данном значении передаваемой мощности Po. Амплитуда характеристики мощности Pm возрастает.

Критерии устойчивости СД:

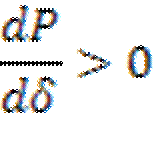
35. Изменение частоты системы и влияние на устойчивость асинхронной нагрузки

Значения Р и Q при изменении подводимого U влияет на условия опрокидывания двигателей при Mc=сonst, а Р на валу двигателя изменяется пропорционально частоте (Р=ωМ). Снижение f приводит к уменьшению скольжения

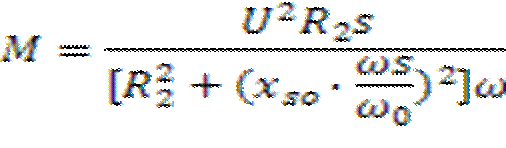
Где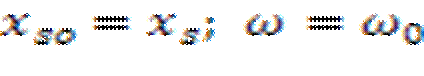

При М=сonst можно грубо заменить зависимостью s=f(ω) прямой и принять s 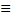f. Однако критическое скольжение при снижении частоты оказывается больше, т.к.

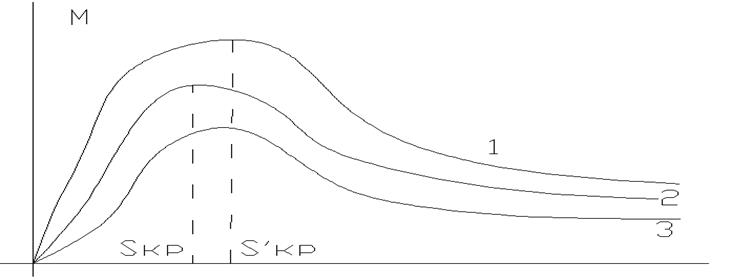
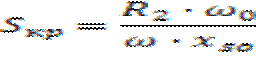Это благоприятно сказывается на устойчивость, тем более, что максимальное значение M несколько увеличивается. Где 1 – снижение f 2 – норм. Режим 3 – снижение U

36.Представление нагрузки в расчетах устойчивости. Статические и динамические характеристики нагрузки.

Переходные процессы в узлах нагрузки могут рассматриваться с двух точек зрения:

1)поведения собственно нагрузки при переходных про­цессах и влияния этих процессов на работу потребителей {например, мигание ламп при колебаниях напряжения в сети, порча продукции при изменении ско­рости двигателей во время изменений напряжения или частоты при переходных процессах и т. п.);

2)влияния переходных процессов в нагрузке на режим системы (например, самозапуск двигателей может привести к недопустимому понижению напряжения в системе, а в неправильно спроектированной системе — даже к нарушению ее устойчивости).

Кроме того, процессы, непрерывно происходящие в какой-либо нагрузке, могут оказывать неблагоприятное влияние на работу остальных потребителей системы (например, толчки в нагрузке, содержащей мощные двигатели прокатных станов, могут приводить к колебаниям напряжения и частоты в системе, понижая качество выдаваемой потребителям энергии).

Основную часть нагрузки (обычно от 50 до 80%) составляют асинхронные двигатели, свойства которых существенно проявляются в характере переходных процессов всего узла системы. Для них, так же как и для синхронных двигателей, различают статические характеристики, т. е. зависимости то­ка |/| или вращающего момента \М\ двигателя от медленно меняющегося сколь­жения его ротора \ s \, и динамические характеристики — зави­симости быстро меняющегося скольжения, напряжения и скорости их изменения (ускорения а) от тока. Так, для асинхронного двигателя

Для синхронного двигателя аналогичная зависимость, определяющая ста­тическую характеристику, будет иметь вид

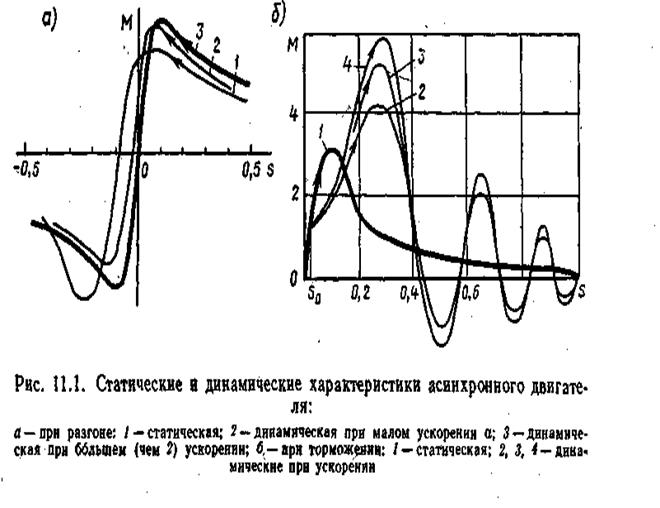
Эти характеристики графически представлены на рис. 11.1 и 11.2.

Процессы при медленных отклонениях от установившегося состояния могут всегда рассматриваться на основе только статических характеристик. Для изуче­ния процессов при быстрых изменениях, т. е. «в динамике», должны применяться динамические характеристики. Однако в ряде случаев и при рассмотрении ди­намических процессов можно пользоваться квазидинамическими, а иногда и ста­тическими характеристиками. Например, при относительно медленных ускорениях асинхронного двигателя и несоизмеримости электромагнитных и электромеха-' нических постоянных времени разница в использовании статических и динами-

ческих характеристик будет невелика (рис. 11.3). Как видно из рисунка, чем мень­ше коэффициент Ki и чем больше так называемая условная скорость изменения скольжения Sy_c„ == 1/С = M_aou /( Ja >0) тем сильнее искажаются статические механические характеристики, становясь здесь динамическими

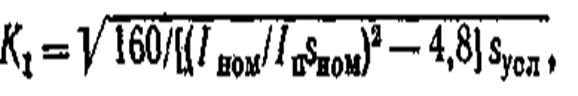
где /_ном и /_п — номинальный и пусковой токи.

При изучении ряда переходных процессов асинхронных двигателей прибли­женно можно считать, что фазовая траектория или динамическая механическая

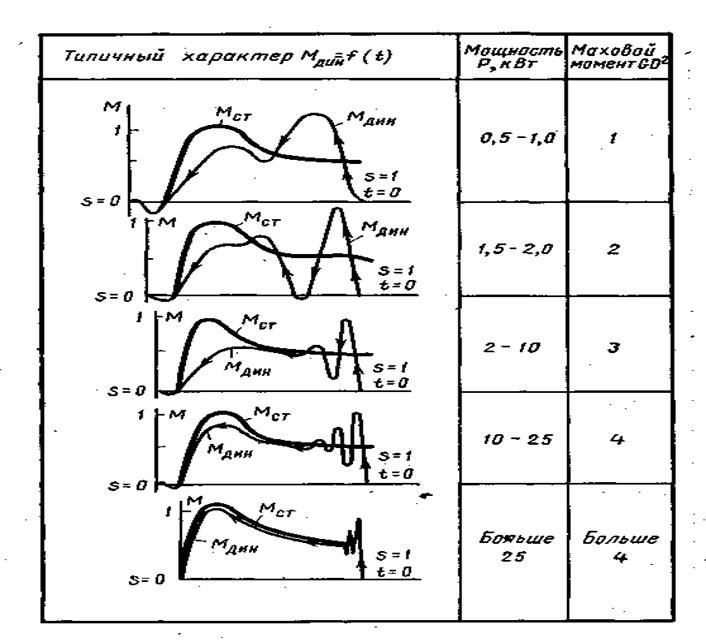
характеристика процесса определяется следующим образом. Принимают, что ди­намический момент, возникающий при любом нестационарном режиме, состоит из двух составляющих: Мдщ, = M_t + M_s , где Mi — составляющая момента, определяемая переходными процессами, связанными с протеканием в обмотках двигателя переходных токов; М₂ — составляющая момента, определяемая как М₂ = К₂М_0Т. Здесь М_сT == f (со) — статическая механическая характеристика, рассчитанная по известной формуле момента асинхронного двигателя:

37.Основные расчетные соотношения асинхронных двигателей. Схемы замещения и механическая характеристика АД.

Представим приближенно всю нагрузку эквивалентным асинхронным дви­гателем. При этом используем статические характеристики асинхронных двигателей и соответственно упрощенные уравнения. Это оправдано, во-первых, тем, что начальные отклонения, обусловливающие появления неустойчивости, предположены малыми, и, во-вторых, тем, что когда в процессе опрокидывания двнигатели приобретают значительную скорость, характер процесса (быстрее, медленнее) не имеет практического значения. В отдельных случаях необходимо переходить к полным уравнениям, т. е. динамическим характеристикам.

Рассмотрим с учетом отмеченного схему системы (рис. 11.7, а), где сопротивление генератора хг_г, сети х_с и эквивалентного двигателя, заменяющего все двигатели нагрузки х _s , соизмеримы по величине. Представим схему замещения так, как это показано на рис. 11.7, б. Затем приближённо упростим ее, перенеся левую точку , к месту приложения э. д. с Е (рис. 11.7, в).

Ток, обусловленный э. д. с. в цепи 1-2 (рис. 11.7, в),

Далее запишем

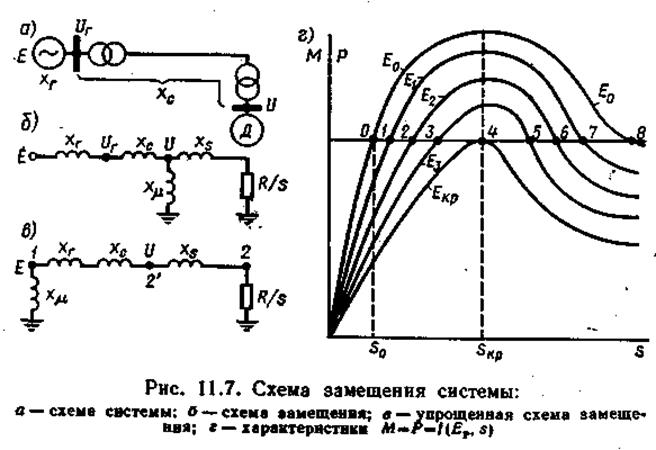
Характеристики Р = /(E, s ) построены на рис. 11.7, г, где значение критического скольжения двигателя определяется из условия dPIds — 0. Дифференцируя и приравнивая нулю (11.1), получаем

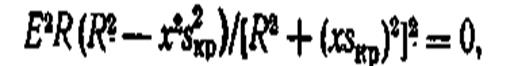
откуда skp = R / x . Подставив значение s_Kp в (11.1), найдем значение Р_т, отвечаю­щее s_Kp: