1 пропорционального действия (изменяют ток возбуждения пропорционально отклонению какого-то параметра)

Дата: 2025-06-15; Просмотры: 1

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

2 сильного действия (реагируют не только на отклонение параметров режима, но также и на скорость и ускорение их изменений, причём в системе возбуждения, в которую как составляющая входит АРВ СД, элементы должны обладать малой инерционностью, что позваляет получить быстро изменяющийся ток возбуждения.

15.Характеристики мощности генераторов с АРВ. Упрощенное представление генераторов в расчетах устойчивости.

Под системой регулирования возбуждения понимают аппараты для создания тока возбуждения и управления ими с помощью устройств АРВ, которые применяются для регулирования возбуждения, разделяются на регуляторы осуществляющие прерывистое и непрерывное действие регулирования (без зоны нечувствительности) – если точка в исх. зоне нечувствительности то регулятор не работает. На крупных генераторах работающих в энергосистемах в настоящее время применяются регуляторы непрерывного действия: 1) регуляторы пропорционального действия, изменяющие ток возбуждения пропорционально отклонению какого-либо параметра режима; 2)регуляторы сильного действия реагирующие не только на отклонение параметров режима, но и на скорость и ускорение (1ю и 2ю производные их изменений.

АРВ пропорционального действия изменяют Ег пропорционально входному сигналу (ΔU) – E=Eo+K ΔU. С помощью регуляторов пропорционально действия практически можно поддерживать постоянной переходную ЭДС – Ed’, за переходным сопротивлением генератора Xd’.

АРВ сильного действия изменяет Ег в зависимости от ΔU и производных 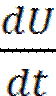и 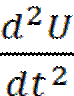. E=Eo+K1ΔU+K2 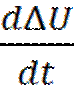+K3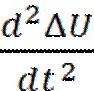

т.е. регулирование наводиться не только по отношению но и по условию входного сигнала. С помощью регулятора сильного действия можно поддерживать постоянное напряжение на зажимах генератора или в начале линии за повышающими трансформаторами. Pг = 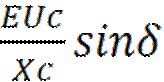– предел мощности. При наличии АРВ пропорционально действия Е =Еd’ Хг = Xd’ При наличии АРВ сильного действия Uг =const Xг = 0, Xc возрастает в АРВ пропорционального действия и уменьшается в АРВ сильного действия.

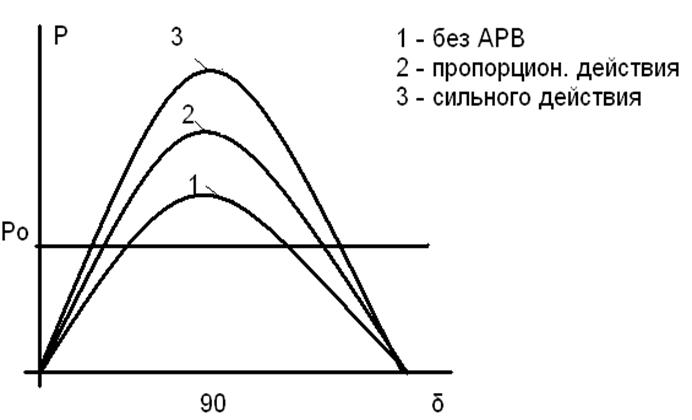
В установившемся режиме схема замещения генератора представляется синхронным ЭДС и и синхронным сопротивлением .

16. Характеристика мощности явнополюсных синхронных машин.

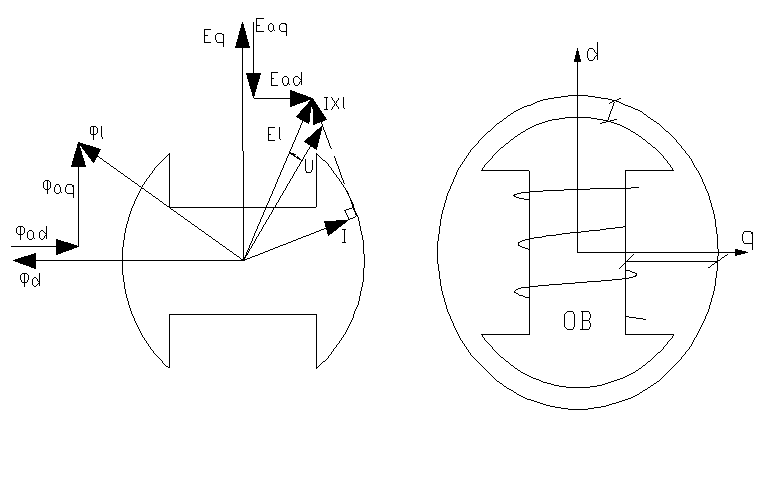
x_d; x_q- т.к. воздушные зазоры разные (Xd > Xq)

Схема замещения генератора была представлена в виде ЭДС и синхронной индуктивности сопротивления через которое протекает полный ток генератора. Такая схема допустима для неявнополюсного генератора, в которых сопротивление по продольной и поперечной оси практически одинаково. У явнополюсных генераторах Xd и Xq значительно отличаются, поэтому при более точных расчетах необходимо строить две схемы замещения генераторов. В определенных условиях удобно получить зависимость мощности от угла из векторной диаграммы явнополюсного генератора. В режиме хх ток возбуждения генератора создает магнитный поток основная часть которого пронизывает воздушный зазор и пересекает обмотки статора и наводит в них Eq. У нагруженного генератора ток обмотки статора может быть разложен на Id и Iq которые создают магнитные потоки, независимые потоки продольной и поперечной оси реакции якоря Фad и Фaq вращающихся синхронно с ротором……. и сдвинуты на четверть полного деления. Наводимые потоками реакции якоря Ead и Eaq геометрически складываются с Eq и дают внутреннюю ЭДС генератора E_L, которой соответствует магнитный поток Ф_L.

Индуктивное сопротивление реакции якоря Xad явнополюсной СМ >> Xaq т.к. продольный магнитный поток встречает меньшее сопротивление воздушного промежутка Фd. Неравенство Xad и Xaq приводит к тому что необходимо разлаживать падения U в индуктивном сопротивлении генератора на 2 составляющие Zaq*X_L и Zad*X_L

Обозначим Ψ=( Eq^I)

P=U*I*cosφ+I*cosφ*U*cosδ+I*sinφ*U*sinδ

Eq=Id*Xd=Uq Iq*Xq=Ud

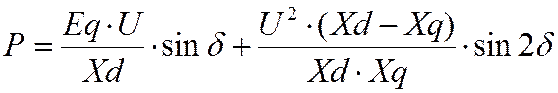
Нюансы: 1) δ_кр < 90⁰ уменьшается зона устойчивости

2) увеличивается идеальный предел P и Pm. Амплитуда сост-щей удвоенной f не превышает 10—15% от основной. И про рассматриваемом норм. режимов (иногда п/ав) можно пренебречь 2-й составляющей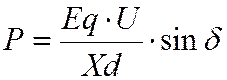

При рассм. ав/ режимов, когда величена ампл-ды 1-й сост-щей низка а ампл. 2-й f заметно влияет на угловую хар-ку. Для упрощения расчетов 2-ю составляющую не учитывают

17. Расчет статической устойчивости простейшей системы. Коэффициент запаса . Практические критерии устойчивости.

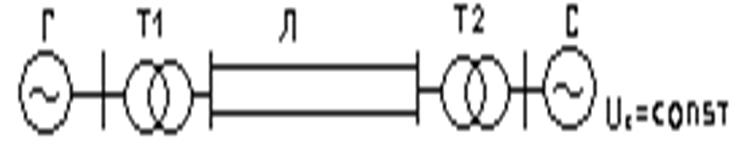
На шинах системы модуль U и его фаза неизменны

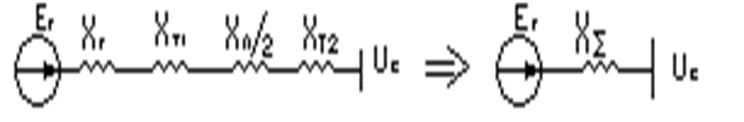
Х∑=Хг+Хт1+Хл/2+Хт2, Iс∙Х∑=Еsinδ, Uc∙Ic=(Uc∙Е/ Х∑)∙sinδ=P - мощность выдаваемая генератором

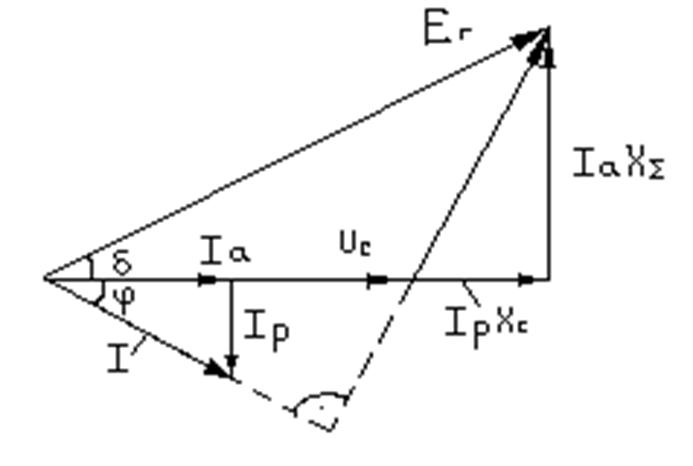
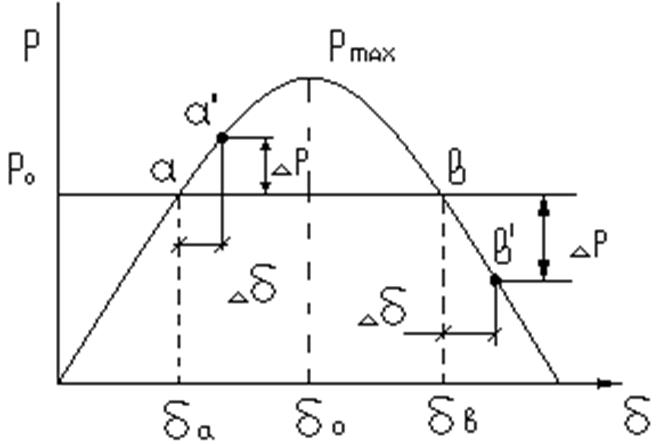
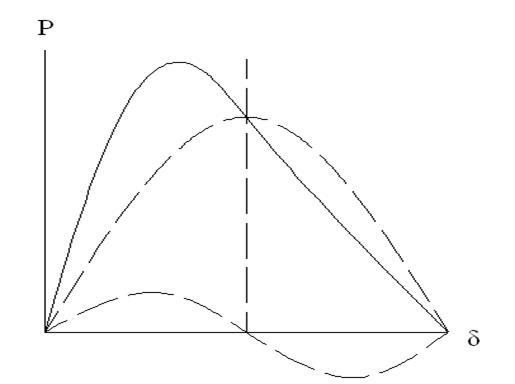
Мощность выдаваемая генератором в сеть зависит от δ.

Если возникает избыток мощности то генератор начинает ускорятся .Получается новая точка равновесия если ее не существует, то генератор выпадает из синхронизма или отключен защитой. Если точка равновесия существует , то пройдя эту точку генератор начнет тормозится в точке (а)-тормозится в точке (в) ускоряться / Рмах=(Uc∙Е/ Х∑) – идеальный предел мощности/

Все точки устойчивого равновесия находятся на восходящей части синусоиды 0÷90, зона от 90÷180 является неустойчивой работы. Статическая устойчивость – способность системы самостоятельно восстанавливать исходный режим работы при малом возмущении. Важные условия статической устойчивости: для устойчивости системы необходимо и достаточно чтобы приращение угла и мощности Рг имели один и тот же знак т.е. ∆Рг/∆ δ>0, или переходя к пределу dPг/d δ>0, это условие выполняется при 0≤ δ≤90

Кз=(Рн-Ро)/Ро – коэф-т запаса по мощности

Кз= (δ- δо)/ δo – коэф-т запаса по углу

18. Метод малых колебаний при анализе статической устойчивости.

Основные положения метода заключаются в подаче небольших возмущений системе и анализе возникновения свободных колебаний. Т.к. характеристики ДУ является нелинейный, то при анализе применяется методы линеаризации. Приводя исходные ДУ к линейному ДУ с постоянными коэффициентами. При решении необходимо разрешить характеристическое уравнение выявить постоянные интегрирования. При анализе устойчивости чаще всего не требуется находить решение ДУ. Анализируются корни характеристического уравнения

Тj∙(d²δ/dt²)=Po-Pm∙sinδ

. Если даем толчок, изменяем характеристику, то возникают

∆Р=Ро- Pm∙sinδ – небаланс.

При малых колебаниях ротора разложим ∆Р в ряд Тейлора в окрестности точки δ_о. При малых ∆δ числами второго, третьего и высшего порядка пренебрегаем.

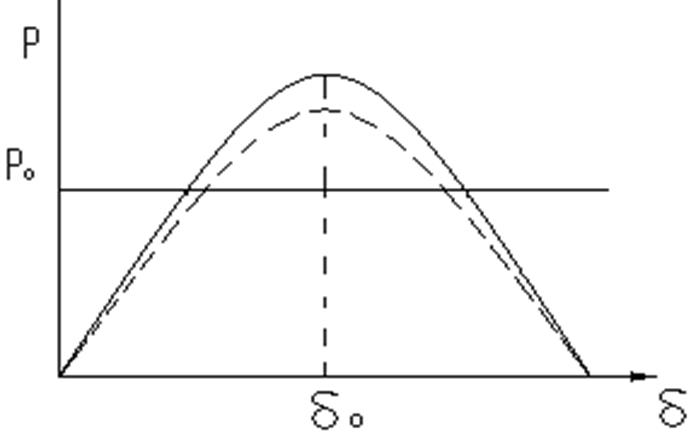
В результате решения получаем уравнение:

(d²∆δ/dt²)+(1/Tj)∙(dP/dδ)∙∆δ=0

,решение ∆δ=К₁е^Р1t+К₂е^Р2t

Характеристическое уравнение :

P²+(1/Tj)∙(dP/dδ)=0,

где решением является

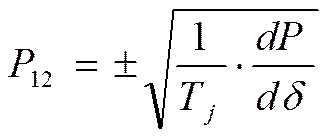
Корни характеристического уравнения – при линейные при dP/dδ>0 Либо корни вещественные, равные по модулю и разные по знаку. При линейных корнях ∆δ=Сsin(ωt+ψ) Изменение угла происходит вокруг δ₀ по синусоиде, незатухающий характер колебанй связан с неучетом потерь эл.энергии в исходных ДУ. Из-за потерь энергии в электрической и механической части генераторов колебания затухнут и установится прежний или новый режим ∆δ=К₁е^µt+ К₁е^µt . Следовательно необходимым и достаточным условием устойчивости работы генератора является положительность синхронизирующей мощности dP/dδ. При неучете активных сопротивлений статическая устойчивость нарушается при углах > 90, где колебания угла приобретают непериодический характер и генератор выходит из синхронизма.

19. Виды нарушения устойчивости нерегулируемой системы. Сползание режима, самораскачивание и самовозбуждения.

Частный случай, когда в системе предполагается отсутствие регулирования возбуждения и не учитывается переходные процессы, представляют интерес для выяснения влияния этих факторов на предел передаваемой мощности. Учтем демпферный момент упрощенно (Рd). В этом случае переходной процесс в системе будет описываться одним нелинейным ДУ второго порядка:

Tj∙P²∙δ+Pd∙Pδ=Pт-Рэ;

Рт=Ро-Рм∙sinδ_o – мощность турбины.

Рэ=Рм∙sinδ–эл.магн.мощность генератора

Раскладываем Рм∙sinδ в ряд Тейлора по малой величине ∆δ в окрестности δ_о . После преобразования полученной лианелизацией, по первому приближению диф. уравнения.

Tj∙P²∙∆δ+Pd∙P∆δ+Сi∙∆δ=0.

Решение ∆δ=А₁е^Р1t+А₂е^Р2t ;

Характеристическое уравнение:

Tj∙P²+Pd∙p+Ci=0

имеет два корня Р_1,2=±jΨ+α,

где – собственная частота колебаний ротора генератора.

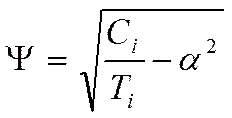
α=-(Рd/2Tj) – определяет затухание. При С<0 оба корня характеристического уравнения-действительны и один из них всегда положительный ; при всяком возмущении в системе будет происходить апериодическое нарастание угла. Угол δ_о = 90 – является приделом статической устойчивости, границей разделения двух видов движения : колебательное при δ_о < 90 и апериодическое при δ_о > 90. При δ_о > 90 в системе происходит апериодическое нарушение статической устойчивости –это называется сползанием режима(изменение параметров режима). Область, где Сi >0 – сектор, где незатухающие колебания перейдут в затухающие. Условие Сi >0 – отвечает практическому критерию устойчивости dP/dδ=0. Проведенное исследование не является полным – т.к. не рассматривается нарушение устойчивости, имеющее специфическое характер самораскачивания и самовозбуждения. Такие нарушения могут наступать при наличии в сети или заметного активного сопротивления (x/r>0,05), или емкости(-Тd^I) в первом случае возникнут установившиеся или нарастающие колебания ; во втором происходит самопроизвольный рост тока и напряжения генераторов, потребляющих емкостную (-Q) реактивную мощность – самовозбуждения может происходить при подключении генератора к ненагруженной (отключенной от системы ) ЛЭП. В действительности нарастание тока будет ограниченно насыщением магнитных цепей генератора и трансформатора. Нарастание тока будет сначала монотонно(синхронное самовозбуждение) и асинхронное самовозбуждение – сопровождаться биением.

20. Понятие динамической устойчивости системы. Основные допущения при упрощенном анализе.

Электрическая система, обеспечивающая своим нормальным функционированием работу промышленности, трансформатора, быта населения, должна работать надежно. Основным условием надежной работы является ее устойчивость – способность системы восстановить свое исходное состояние.

Различают два вида устойчивости: статическую устойчивость и динамическую устойчивость, рассматриваемую при больших (обычно нелинейных) отклонениях параметров n 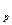часто сопровождающихся изменениями конфигурации и параметров электрической системы и значений их параметров.

Различают два вида динамической устойчивости: синхронную устойчивость – сохранение режима при больших колебаниях, но без поворота ротора генератора (180 – 360 градусов);

результирующую устойчивость – восстановление режима после кратковременного нарушения (работа генератора несинхронно), но при восстановлении нормальной синхронной работы после нескольких поворотов ротора. Это восстановление может происходить самостоятельно в силу внутренних свойств системы и под действием специальных устройств системной автоматики.

Для обеспечения устойчивости система должна работать с некоторым запасом, характеризуемым коэффициентом запаса Кз, т.е. при таких параметрах режима которые отклоняются в Кз>1 от критических – тех при которых может произойти нарушение устойчивости. Для определения Кз в данной системе параметры которой известны, и для выбора мероприятий, улучшающих устойчивость, необходим анализ (расчеты) устойчивости с определением критических параметров.

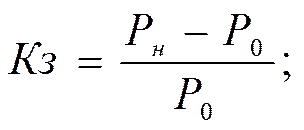
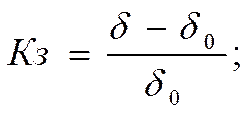
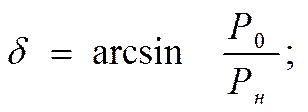
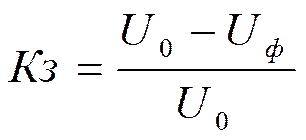
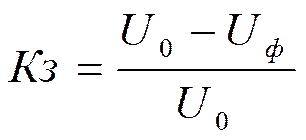
21. Динамическая устойчивость станции, работающей на шины бесконечной мощности. Правило площадей и вытекающие из него критерии устойчивости.

Рассмотрим простейший случай работы электростанции через двухцепную ЛЭП на шины бесконечной мощности. Постоянство напряжения на шинах системы по модулю и по фазе исключает возможность качаний приемной системы.

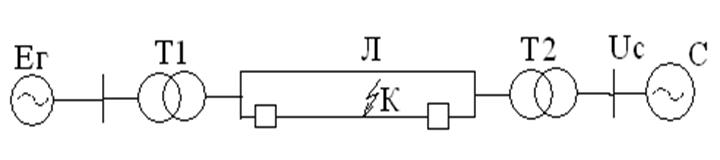
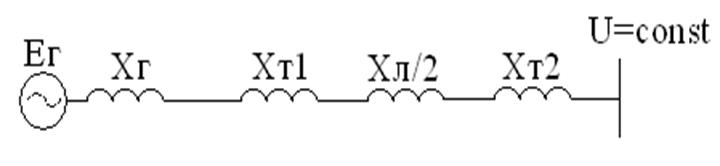
ХΣ=Хг+Хт1+Хл/2+Хт2

Хг - переходное сопротивление генератора

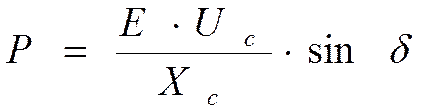
Е- переходное ЭДС генератора

Хк – эквивалентное шунтирующее сопротивление КЗ состоящее из сопротивлений обратной и нулевой последовательностей. В связи с изменением конфигурации схемы в случае КЗ при неизменной Ег за переходным сопротивлением, значение передаваемой мощности генератора изменяется.

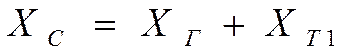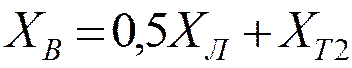; , для однофазного КЗ 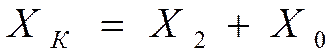, для двухфазного КЗ 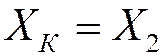, для К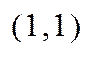 , Ү 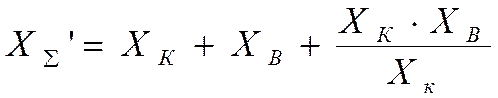. Весь поток мощности генератора искривляется через 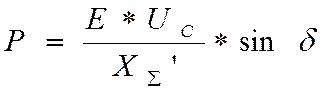. Зависимость мощности от угла имеет синусоидальный характер, но амплитуда ее меньше, чем при нормальном режиме. Приведенные характеристики дают возможность определить максимальное отклонение угла, которое и указывает сохранила ли система устойчивость. В рассматриваемом случае избыточный момент сначала ускоряет вращение ротора и работа совершенная в период ускорения равна 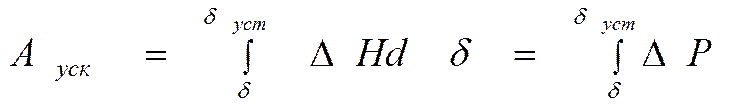После того как ротор найдет точку своего установившегося положения на новой характеристике мощности, избыточный момент меняет свой знак и начинает тормозить вращение ротора. Изменение климатической энергии в период торможения при перемещении ротора от 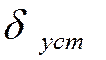до 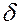равно:

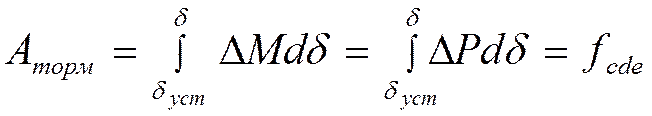
Площадь f_cde называется площадью торможения. 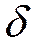_{откл –} определяется равенством f_уск и f_торм.

Критерий динамической устойчивости F_УСК=F_торм.

22. Анализ динамической устойчивости при отключении короткого замыкания. Предельный угол отключения КЗ. Предельное время отключения.

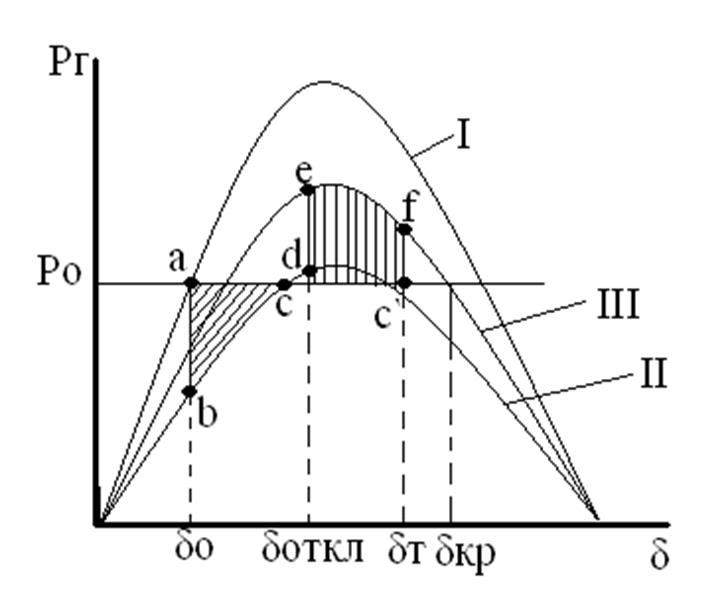
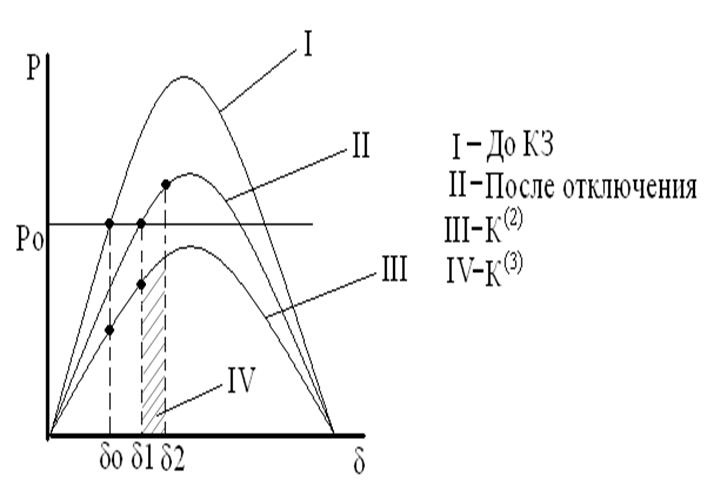
В момент КЗ передаваемая мощность падает, и ротор начинает ускоряться. Пусть в некоторой точке d происходит отклонение поврежденной цепи. В момент включения работа переходит в точку L на кривой III, и в результате отдаваемая генераторами мощность значительно повышается. Благодаря этому максимально возможная площадь торможения (ограниченная кривой с,d,e,f,c’) получается значительно больше, чем при длительном неотключенном КЗ, и это увеличение тем больше чем раньше происходит выключение, т.е. тем чем меньше угол δ откл. Благодаря своей простоте и большому эффекту это средство находит широкое применение и является по существу основным мероприятием, служащим для повышения динамической устойчивости.

С помощью рисунка, пользуясь правилом площадей можно графически найти предельное значение угла δ откл. Значение этого угла определяется равенством площади ускорения и возможной площади торможения.

δ откл. легко можно найти аналитически, т.е. приравнивая нулю сумму площади ускорения и максимально возможной площади торможения:

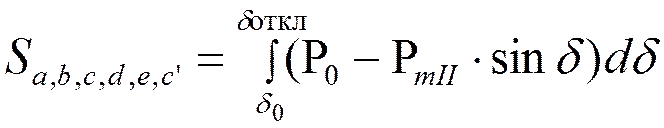
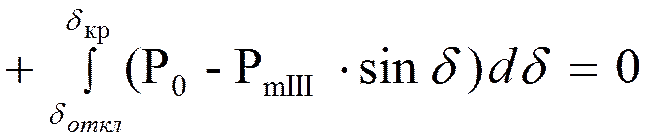
где Р_mII и P_mIII - амплитуда характеристик мощности при КЗ и отключении цепи.

Преобразуем:

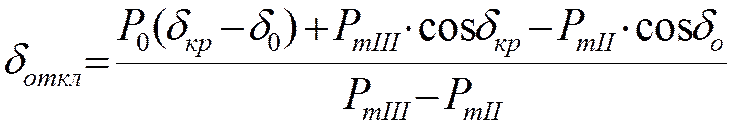
Однако для практических целей, т.е. чтобы предъявить выключателю и РЗ те или иные требования в отношении скорости отключения, необходимо знать не угол δоткл., а только промежуток времени, в течении которого ротор успевает достигнуть этого угла, т.е. предельное время отключения.

Метод последовательных интервалов:

1.

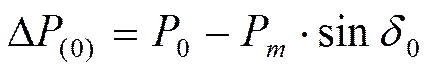
2.

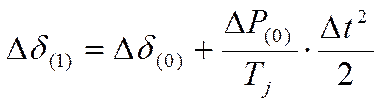
3.

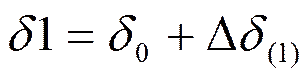
где ΔP_(i) – разность между мощностью первичного двигателя и мощность отдаваемой генератором в сеть.

Δδ_(i) – приращение угла в i-ом интервале

δ_(i) – угол отключения в i-ом интервале

Δt – при ручном счете принимается 0,05с. Если ожидать, что амплитуда колебаний будет не велика, то Δt может быть повышено до 0,1с.

Расчет методом последовательных интервалом ведется до тех пор пока δ не начнет уменьшаться или пока не будет ясно, что угол беспредельно возрастает, т.е. что машина выпадает из синхронизма.

23. Методика расчета динамической устойчивости сложных электрических систем. Метод численного интегрирования.

При возникновении КЗ в сложно системе (с учетом нескольких генераторов 3 и более) возникают качания роторов в генераторах. При моделировании данного процесса можно написать систему дифференциальных уравнений движения роторов каждого генератора. Основным методом решения диф уравнений являются квадратурные методы включая метод последовательных интервалов. При отсутствия систем моделирования на ЭВМ необходимо учитывать собственные и взаимные сопротивления для определения электромагнитной мощности генераторов. Собственные и взаимные индуктивности можно определить методом наложения, в том числе методом единичных токов.

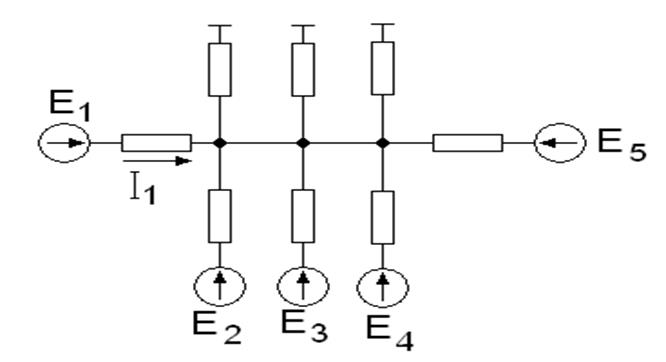
Активная мощность первого генератора определяется:

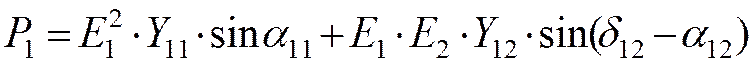
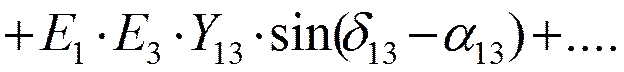
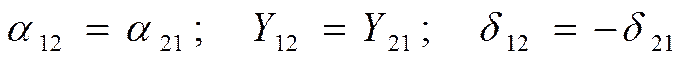
Порядок расчета динамической устойчивости сложных систем:

1) Находятся параметры нормального режима (Е₁, Е₂…δ)

2) Рассчитывается режим КЗ. Составляющая 3х схем последовательностей и результирующая схема.

3) Находятся собственные и взаимные проводимости для расчета режима КЗ.

4) Находим собственные и взаимные сопротивления для послеаварийного режима при отключении КЗ.

5) Применяют метод последовательных интервалов для момента возникновения КЗ.

6) Зная абсолютные углы δ₁, δ₂, δ₃ определяют относительные углы δ₁₂, δ₂₃, δ₁₃.

7) Определяют активные мощности генераторов при КЗ.

8) Определяют избытки или недостатки мощности.

9) Определяют угловые перемещения за промежуток времени Δt.

10) Определяю абсолютные значения углов к концу первого интервала δ₁, δ₂, δ₃.

11) Повторяем пункты 6-10.

В интервале времени в котором КЗ определяется необходимо в формулах сменить собственные и взаимные проводимости и углы α.

24. Результирующая устойчивость. Причины возникновения асинхронного хода. Особенности исследования результирующей устойчивости.

Динамическая устойчивость – это способность системы восстанавливать после большого возмущения исходное состояние или состояние практически близкое к исходному (допустимому по условиям эксплуатации системы).

Различают два вида динамической устойчивости:

1) синхронная устойчивость. 2) результирующая устойчивость – восстановление режима после кратковременного нарушения (например, при работе в течении некоторого времени генераторов электрической системы или ее части несинхронно), но при восстановлении нормальной синхронной работы после нескольких проворотов ротора. Это восстановление может происходить самостоятельно в силу внутренних свойств системы или под действием специальных устройств автоматики.

Причины возникновения асинхронного режима генераторов или части системы (группы генераторов) могут быть различны. Его может вызвать исчезновение (потеря) возбуждения, нарушение динамической устойчивости после резкого возмущения – только при нарушении статической устойчивости сильно перегруженной системы при малом возмущении.

Для большинства синхронных машин асинхронный ход не представляет опасности. Турбогенераторы в асинхронном режиме могут развивать мощность, соизмеримую с номинальной.

Допустимость асинхронного режима может вызывать сомнения в связи с опасностью нарушения устойчивости остальной части системы в которой мощный генератор или группа генераторов работают асинхронно. В этом режиме генератор обычно поглощает из системы значительную реактивную мощность, это приводит к снижению напряжения во всей системе создавая опасность нарушения устойчивости остальных генераторов и двигателей.

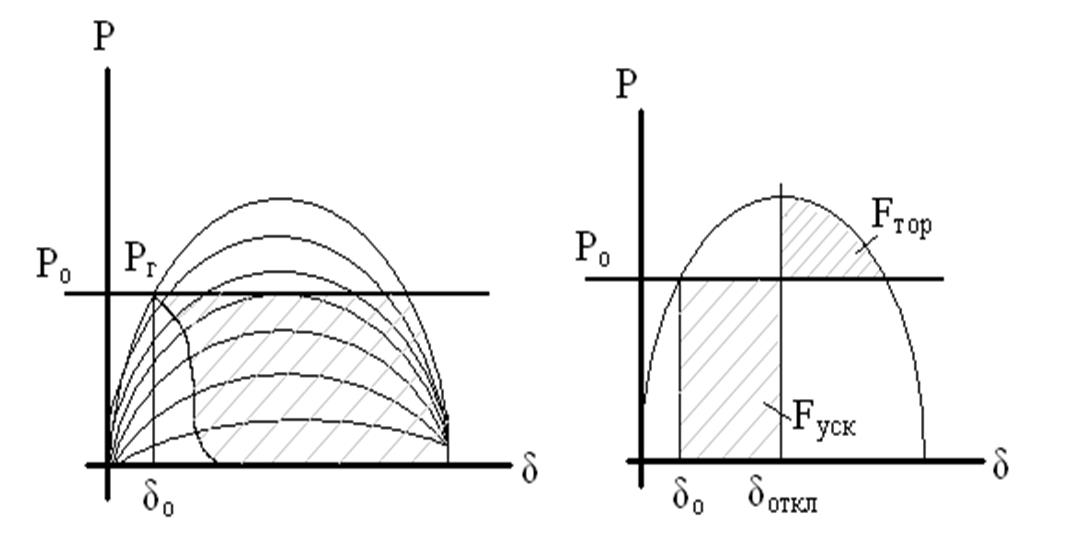
При потере возбуждения При нарушении динамиче- с ской устойчивости (F_тор≠F_уск)

25. Общая характеристика переходных процессов в узлах нагрузки. Большие и малые возмущения в системах электроснабжения.

Часть энергетической системы, непосредственно осуществляющая снабжение электрической энергии потребителей, называется системой электроснабжения.

Места подключения отдельных систем электроснабжения к высоковольтным сетям электрических систем, называют узлами нагрузок.

Переходные процессы в системах электроснабжения можно различать по виду возмущений (малое, большое, длительное,…), так же как это делалось для системы в целом. Так в нормальном режиме система при малых его возмущениях возникает необходимость проверки плановой установки синхронных двигателей, синхронных компенсаторов и больших групп АД, которые, имея мощность, соизмеримую с мощностью питающих их генераторов могут оказаться не устойчивыми.

При чем эта неустойчивость проявляется в виде специфического явления называемого лавиной напряжения. Пуски двигателей, резкие колебания момента на валу, и т.д., приводит к изменению значения и фазы напряжения в узлах нагрузки. Отклонение величин не должны превышать допустимых пределов. Влияние резких изменений режимов двигателей обычно заметно проявляется в распределительных сетях в виде колебания напряжения.

Такие нарушения режима, как КЗ в элементах питательных сетей отключение и повторное включение двигателей, самозапуск АД, и т.д. могут существенно сказаться на режиме всей системы электроснабжения, поэтому переходные процессы в элементах рассматриваются не только с точки зрения обеспечения их надежности, но и с точки зрения обеспечения надежности всей системы.

Переходные процессы в узлах нагрузки могут рассматриваться с двух точек зрения:

1)Поведение собственно нагрузки, при переходном процессе и влияние этих процессов на работу потребителей(питание потребителей при колебаниях напряжения в сети, порча продукции при изменении скорости двигателей во время изменения напряжения или частоты при переходном процессе);

2)Влияние переходных процессов в нагрузке режим системы (самозапуск электродвигателей – приводит к недопустимому понижению напряжения в системе)