Недостоверность выборочной разности говорит о том, что ничего нельзя заключить с заданной надежностью о генеральной разности. Между генеральными средними могут иметься любые соотношения.
Для определения достоверности выборочной разности средних рассчитывается критерий достоверности разности по формуле
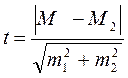
Затем по табл.15.1 находят стандартные значения критерия надежности по Стьюденту (tst) для трех порогов вероятности безошибочных прогнозов в соответствии со степенью свободы критерия, который определяется по формуле g=n1+n2-2
Рассчитанный критерий t и три значения tst сравнивают между собой. Если t ≥ tst для определенного порога вероятности, то разность достоверна. Если t < tst, то разность недостоверна, следовательно осталось недоказанным как наличие, так и отсутствие разности между генеральными средними.
Исходные данные: V 1 , V 2 -первичные даты (эмпирическое значение признака).
Используемые формулы:
Средняя арифметическая М=åV / n ;
Дисперсия С=åV 2 -(åV )2/ n;
Варианса d= Ö ( C /( n -1));
Ошибка репрезентативности m =d/ Ö ( n );
Разность средних по Стьюденту t =| M 1 - M 2 |/ Ö ( m 1 2 + m 2 2 );
Пример решения задачи.
Отличается ли содержание СО2 (мг/м3) в воздухе рабочей зоны цеха автотранспортного предприятия при различных способах устройства газоочистного и газоотводящего оборудования. Исходные данные – концентрации СО2 (мг/м3), полученные в результате замеров в течении рабочего дня при различных способах очистки воздуха (V1 и V2).
| n | V1 | V2 | V1*V1 | V2*V2 |
| 1 | 12 | 9 | 144 | 81 |
| 2 | 9 | 8 | 81 | 64 |
| 3 | 10 | 5 | 100 | 25 |
| 4 | 13 | 2 | 169 | 4 |
| 5 | 15 | 10 | 225 | 100 |
| 6 | 14 | 10 | 196 | 100 |
| 7 | 8 | 6 | 64 | 36 |
| 8 | 12 | 14 | 144 | 196 |
| å | 93 | 64 | 1123 | 606 |
M1=93/8=11,63 C1=1123-932/8=41,88 d1=Ö (41,88/7)=2,44 m1=2,44/Ö (8)=0,86
M1± m1=11,63 ±0,86 мг/м3
M2=64/8=8,00 C2=606-642/8=94,00 d2=Ö (94,00/7)=3,66 m2=3,66/ Ö (8)=1,29
M1± m1=8,00 ±1,29 мг/м3
t=|11,63-8,00|/Ö (0,862+1,292)=2,34
g=8+8-2=14
Стандартные значения критерия Стьюдента определяем по табл. 15.1.

 tst={2,1-3,0-4,1} t=2,34
tst={2,1-3,0-4,1} t=2,34

Вывод: Содержание оксида углерода в цехе АТП при различных способах газоочистки отличается. Разность достоверна для порога вероятности 0,95.
Задание 3. Определить, существует ли достоверное различие в уровне загрязнений тяжелыми металлами (свинец) на эталонном участке (лес правобережья р. Суры) и в агроэкосистеме, расположенной вблизи автотрассы Москва – Самара. Исходные данные:
| Эталонный участок | 0,001 | 0,0015 | 0,0014 | 0,0009 | 0,0007 | 0,0015 | 0,0023 | 0,0012 |
| Автотрасса | 0,0031 | 0,0024 | 0,0033 | 0,003 | 0,0015 | 0,0013 | 0,0024 | 0,0022 |
Задание 4. Отличается ли загрязненность атмосферного воздуха угарным газом в двух районах города. Исходные данные – концентрация СО в приземном слое атмосферного воздуха
1 район
| Площадь кварталов, га | 3 | 6 | 9 | 1,5 | 8 | 2 | 4 |
| Уровень загрязнения, мг/м3 | 0,75 | 0,64 | 0,15 | 0,44 | 0,96 | 0,22 | 0,21 |
2 район
| Площадь кварталов, га | 2 | 2,5 | 3,4 | 10 | 6 | 3,5 |
| Уровень загрязнения, мг/м3 | 1,25 | 0,84 | 0,97 | 1,11 | 0,94 | 0,45 |
Задание 5. Определить, отличается ли средняя концентрация окислов азота на границе санитарно-защитной зоны от ПДК (0,085 мг/м3). Рассчитать величину погрешности генерального показателя. Исходные данные – протяженность периметра СЗЗ и концентрация NOх на данных отрезках.
| L, км | 0,5 | 1,3 | 1,2 | 1,0 | 1,2 | 1,3 | 0,7 |
| С, мг/м3 | 0,09 | 0,1 | 0,06 | 0,08 | 0,12 | 0,05 | 0,09 |
Табл. 15.1. Значения критерия Стьюдента для 3-х порогов вероятности безошибочных прогнозов
| g | Порог вероятности | g | Порог вероятности | ||||
| 0,95 | 0,99 | 0,999 | 0,95 | 0,99 | 0,999 | ||
| 1 | 12,7 | 63,7 | 637,0 | 13 | 2,2 | 3,0 | 4,2 |
| 2 | 4,3 | 9,9 | 31,6 | 14-15 | 2,1 | 3,0 | 4,1 |
| 3 | 3,2 | 5,8 | 12,9 | 16-17 | 2,1 | 2,9 | 4,0 |
| 4 | 2,8 | 4,6 | 8,6 | 18-20 | 2,1 | 2,9 | 3,9 |
| 5 | 2,6 | 4,0 | 6,9 | 21-24 | 2,1 | 2,8 | 3,8 |
| 6 | 2,4 | 3,7 | 6,0 | 25-28 | 2,1 | 2,8 | 3,7 |
| 7 | 2,4 | 3,5 | 5,3 | 29-30 | 2,0 | 2,8 | 3,7 |
| 8 | 2,3 | 3,4 | 5,0 | 31-34 | 2,0 | 2,7 | 3,7 |
| 9 | 2,3 | 3,3 | 4,8 | 35-42 | 2,0 | 2,7 | 3,6 |
| 10 | 2,2 | 3,2 | 4,6 | 43-62 | 2,0 | 2,7 | 3,5 |
| 11 | 2,2 | 3,1 | 4,4 | 63-175 | 2,0 | 2,6 | 3,4 |
| 12 | 2,2 | 3,1 | 4,3 | 176- | 2,0 | 2,6 | 3,3 |
Контрольные вопросы.
1. Для чего используется средняя арифметическая в экомониторинге?
2. Почему при усреднении данных необходимо вычислять ошибку репрезентативности?
3. Каким уровнем надежности пользуются при расчете погрешности в экологии?
4. Какими способами можно усреднять данные?
5. Как рассчитать разность средних?
6. Как оценить достоверность разности средних?








