Для того чтобы перейти к окну просмотра поверхности выхода выполнить команду System Response/ Section пункта меню Fis в главном окне.
Лабораторная работа № 1
рЕШЕНИЕ ЗАДАЧ УПРАВЛЕНИЯ и наблюдения методами нечеткой логики
Цель работы
Целью лабораторной работы является ознакомление с инструментальным средством FisPro, а также изучение основ проектирования нечетких систем управления с помощью данного программного средства.
1. Краткие теоретические сведения
Нечеткая логика используется в тех случаях, когда построение, а затем и реализация математической модели затруднено, или не представляется возможным по причине сложности моделируемой системы (процесса), наличия неопределенностей, сопровождающих процессы, протекающие в системе.
Основными понятиями нечеткой логики являются понятия: лингвистическая переменная, нечеткие множества, функции принадлежности.
Лингвистическими называются переменные, значениями которых являются термы (слова, предложения). С термином “лингвистическая переменная” можно связать любую физическую переменную, для которой нужно иметь больше значений, нежели, да и нет. Значения лингвистической переменной принято называть термами.
Принадлежность каждого точного значения к одному из термов определяется с помощью функций принадлежности. Существует несколько типов стандартных функций принадлежности: треугольная (trimf), трапецеидальная (trapmf), гауссова (gaussmf), двойная гауссова (gauss2mf), обобщенная колоколообразная (gbellmf), сигмоидальная (dsigmf), произведение двух сигмоидальных функций (psigmf), Z-функция, S-функция, Pi- функция.
В целом процесс вычисления в нечетких системах происходит в несколько этапов:
1) Фаззификация - процесс перехода от “четкого” (измеренного, например 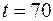 ) значения к “нечеткому” (
) значения к “нечеткому” ( 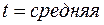 ).
).
2) Нечеткий логический вывод. На данном этапе на основе правил, заложенных на этапе проектирования в базу правил нечеткой системы, происходит определение значения выходной переменной.
Данные правила описывают отношения между лингвистическими переменными с помощью нечетких высказываний, т. е. предложений сформулированных в виде “Если - То” (нечеткие инструкции). При наличии двух входных величин “Если – То” правила состоят из двух условий и объединяются логической операцией AND или OR. Совокупность нечетких правил (нечетких инструкций) принято называть алгоритмом нечеткого вывода. Например, Если t=средняя То P=высокая. Как видно, значение выходной переменной в результате нечеткого логического вывода также является нечетким.
3) На последнем этапе, который принято называть дефаззификацией, осуществляется переход от нечетких значений к четким. Дефаззификация возможна одним из следующих методов: метод центра тяжести, модифицированный метод тяжести, метод максимума, метод левого максимума, метод правого максимума.
2.Описание пакета FisPro
FisPro (Fuzzy Inference System Professional) - это профессиональное программное обеспечение для проектирования, разработки и тестирования систем нечеткого вывода, базирующихся на математическом аппарате нечеткой логики (НЛ). FisPro обладает широкими возможностями для создания и работы систем нечеткого вывода, включая возможности автоматического обучения систем и создания баз нечетких правил, является свободнораспространяемым программным продуктом.
(https://www7.inra.fr/mia/M/fispro/fispro2013_en_download.html).
3. Проектирование нечетких систем в FisPro.
Главное окно программы представлено на рис. 1.1. Здесь в поле Name задается имя системы, в полях Input и Output входные и выходные переменные проектируемой системы.
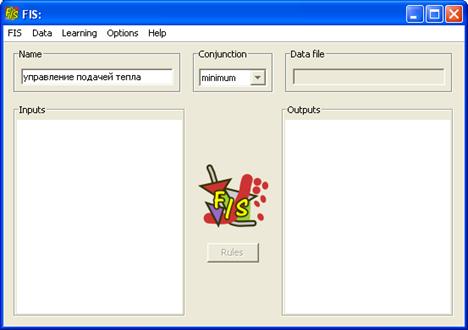
Рис. 1.1. Окно программы FisPro
Рассмотрим этапы проектирования нечетких систем с помощью программы FisPro на следующем примере.
Пример 1. Создать нечеткую систему управления процессом подачи тепла в зависимости от измеренного значения температуры.
1) В самом начале работы необходимо выполнить команды Fis / New и в поле Name задать имя новой системы. Например, «управление подачей тепла».
2) Зададим входные (измеряемые) и выходные (вычисляемые) переменные: для этого нужно выполнить команды Fis, Inputs ( Outputs ), New inputs ( New Outputs ), в открывшемся окне задаем имя переменной, например, «Температура», открыв меню Range, указываем диапазон изменения значений этой переменной (рис. 1.2).
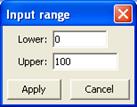
Рис. 1.2. Диапазон изменения значений переменной «Температура»
После нажатия кнопки Apply, нужно выполнить команду MFs / New MFs , чтобы задать термы и функции принадлежности переменной. Здесь (рис. 1.3) в поле Name указывается название терма, Type – тип функции принадлежности (trapezoidal –трапецеидальная функция принадлежности, triangular – треугольная и т.д.)
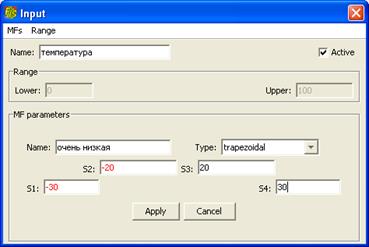
Рис. 1.3
Для лингвистической переменной Температура зададим следующие термы в соответствии с табл. 1.1.
Таблица 1.1
| Название терма (Name) | Тип функции Принадлежности (Type) | Диапазон изменения (Params) |
| Очень низкая | трапецеидальная | [-30 -20 20 30] |
| Низкая | треугольная | [10 30 50] |
| Средняя | треугольная | [30 50 70] |
| Высокая | треугольная | [50 70 90] |
| Очень высокая | трапецеидальная | [70 80 120 130] |
Окно редактора функций принадлежности для переменной «температура» представлено на рис. 1.4.
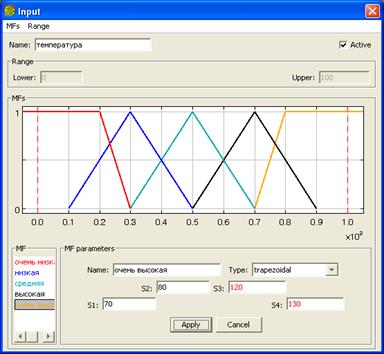
Рис. 1.4 – Термы и функции принадлежности переменной «Температура»
Аналогично задаются термы и определяются функции принадлежности для выходной переменной Подача_тепла (рис. 1.5). Исходные данные приведены в табл. 1.2.
Таблица 1.2
| Название терма | Тип функции принадлежности | Диапазон изменения |
| Очень малая | треугольная | [-20 0 20] |
| Малая | треугольная | [10 25 40] |
| Средняя | треугольная | [30 50 70] |
| Большая | треугольная | [60 75 90] |
| Очень большая | треугольная | [80 100 120] |
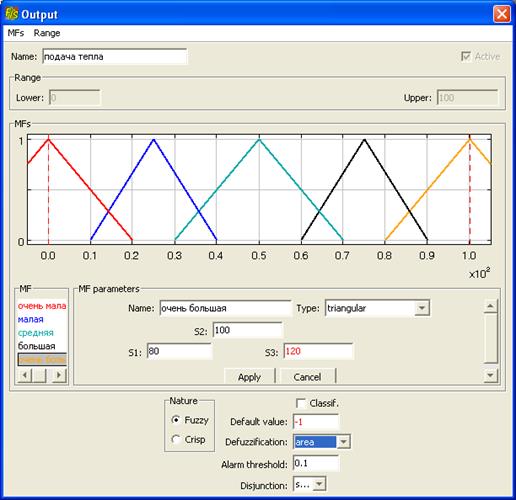
Рис. 1.5
1.3 Чтобы создать базу правил, нужно сначала сформулировать предложения в форме ЕСЛИ – ТО, куда бы входила введенная нами переменная Температура:
ЕСЛИ Температура = очень_низкая То Подача_воды = очень_большая
ЕСЛИ Температура =низкая ТО Подача_воды =большая
ЕСЛИ Температура = средняя ТО Подача_воды = средняя
ЕСЛИ Температура = высокая ТО Подача_воды = малая
ЕСЛИ Температура = очень_высокая ТО Подача_воды = очень_малая
Чтобы внести эти правила в базу правил необходимо нажать на кнопку Rules в главном окне программы, далее выполнить команду New Rule меню Rules.
На рис. 1.6 изображено окно редактора базы знаний после ввода 5 правил.
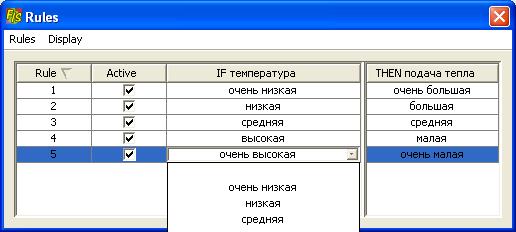
Рис. 1.6. Окно редактора базы правил
1.4 После того как база правил создана можно приступить к этапу логического вывода, для этого нужно выполнить команду Infer меню FIS в главном окне программы.
В левой части окна в графической форме представлены функции принадлежности входной переменной Температура, в правой – выходной переменной Подача_тепла (рис. 1.7). Изменять значения входной переменной можно передвигая бегунок или же задавать числовые значения непосредственно в поле Температура.
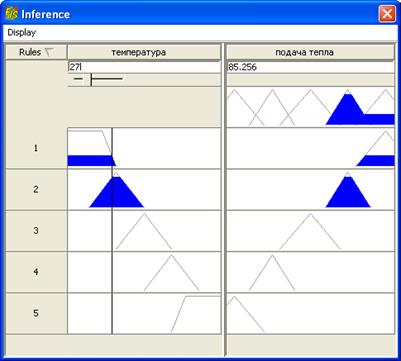
Рис. 1.7. Логический вывод
1.5 Просмотр поверхности выхода.
Для того чтобы перейти к окну просмотра поверхности выхода выполнить команду System Response/ Section пункта меню Fis в главном окне.
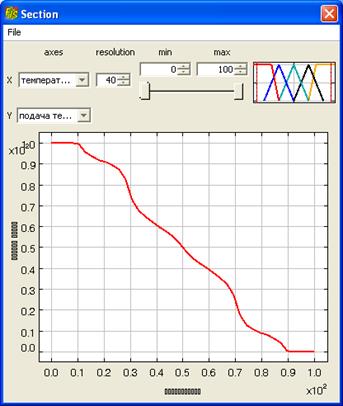
Рис. 1.8. Просмотр поверхности выхода
Пример 2. Построить непрерывную зависимость между двумя наблюдаемыми переменными технологического процесса на основании их дискретных реализаций.
Задача заключается в построении нечеткой аппроксимирующей системы, отображающей зависимость между переменными x и y, заданную с помощью табл. 1.3.
Таблица 1.3
| x | -1 | -0.6 | -0.4 | 0 | 0.5 | 0.7 | 1 | 2 | 4 |
| y | 1 | 0.37 | 0.15 | 0 | 0.24 | 0.5 | 1 | 4 | 16.5 |
1. Создать новую нечеткую систему «аппроксимация функции».
2. Назвать входную переменную как x, выходную как y. Задать диапазоны изменения аргумента и значения функции.
3. Перейти в редактор функций принадлежности переменной х. В качестве типа функции принадлежности выбрать – гауссова функция принадлежности, в полях Name и Mean задать исходные значения переменной x из таблицы, в поле standard deviation указывается «отклонение».
Задать функции принадлежности для выходной переменной y: тип функций принадлежности – discrete, в поле defuzzification указать sugeno (т.е. дефаззификация выполняется по алгоритму Сугено), в поля Name и Value ввести указанные в таблице значения переменной y.
4. Задать правила нечеткого вывода в редакторе правил.
5. Открыть окно нечеткого вывода. Проверить, как система определяет значения выходной переменной.
6. Посмотреть поверхность выхода.
4. Задания к лабораторной работе
4.1 Создать модель движения автомобиля по трассе.
Входные величины:
1. расстояние от автомобиля до препятствия (изменяется в пределах от 0 до 500),
2. скорость автомобиля (0 - 200).
Выходная величина:
Сила торможения (0 - 100).
Термы для лингвистических переменных расстояние и скорость: очень_мало (VS), мало (S), средне (M), велико (B), очень_велико (VB).
Для лингвистической переменной сила_торможения задать следующие термы: близка_к_нулю (Z), четверть (OQ), половина (H), три_четверти (TQ), полная (FU).
Выбор формы функции принадлежности и диапазон изменения термов осуществляется аналогично случаю с одной входной переменной.
Исходные данные для моделирования представлены в табл. 1.4 – 1.7:
Таблица 1.4
Переменная “Скорость”
| Название терма (NAME) | Тип функции принадлежности (TYPE) | Диапазон изменения (PARAMS) |
| Очень малая (VS) | трапецеидальная | [0 0 20 60] |
| Малая (S) | треугольная | [20 60 100] |
| Средняя (M) | треугольная | [60 100 140] |
| Большая (B) | треугольная | [100 140 180] |
| Очень большая (VB) | трапецеидальная | [140 180 200 200] |
Таблица 1.5
Переменная “Расстояние”
| Название терма (NAME) | Тип функции принадлежности (TYPE) | Диапазон изменения (PARAMS) |
| Очень малая (VS) | трапецеидальная | [0 0 50 150] |
| Малая (S) | треугольная | [50 150 250] |
| Средняя (M) | треугольная | [150 250 350] |
| Большая (B) | треугольная | [250 350 450] |
| Очень большая (VB) | трапецеидальная | [350 450 500 500] |
Таблица 1.6
Переменная “Сила торможения”
| Название терма (NAME) | Тип функции принадлежности (TYPE) | Диапазон изменения (PARAMS) |
| Близка к нулю (Z) | трапецеидальная | [0 0 10 30] |
| Четверть (OQ) | треугольная | [10 30 50] |
| Половина (H) | треугольная | [30 50 70] |
| Три четверти (TQ) | треугольная | [50 70 90] |
| Полная (FU) | трапецеидальная | [70 80 100 100] |
Таблица 1.7
База правил для задачи управления силой торможения автомобиля
Скорость
| VS | S | M | B | VB | |||
 VS VS
| H | TQ | FU | FU | FU | ||
| S | OQ | H | TQ | FU | FU | ||
| M | Z | OQ | H | TQ | FU | ||
| B | Z | Z | OQ | H | TQ | ||
| VB | Z | Z | Z | OQ | H | ||
4.2. Создать нечеткую модель контроля уровня воды в баке
Постановка задачи: имеется объект управления в виде бака с водой, к которому подходят две трубы: через одну трубу, снабженную краном, вода втекает в бак, через другую – вытекает. Подачу воды в бак можно регулировать, больше или меньше открывая кран. Контролировать уровень воды в баке можно, например, на основе следующих правил:
1) ЕСЛИ уровень соответствует заданному ТО кран без изменения
2) ЕСЛИ уровень низкий ТО кран быстро открыть
3) ЕСЛИ уровень высокий ТО кран быстро закрыть
4) ЕСЛИ уровень соответствует заданному И его прирост положительный ТО кран медленно закрывать.
5) ЕСЛИ уровень соответствует заданному И его прирост отрицательный ТО кран медленно открывать.
5. Требования к отчету
Отчет должен содержать титульный лист, цель работы, задания на лабораторную работу, исходные данные для моделирования; графики функций принадлежности; выводы по работе, ответы на контрольные вопросы.
6. Контрольные вопросы
1. Какие переменные называются лингвистическими?
2. Какие этапы включает в себя процесс проектирования нечетких систем?
3. В чем заключается процесс фаззификации?
4. В чем заключается процесс дефаззификации?
5. Какие методы дефаззификации были использованы при построении нечетких систем? В чем эти методы заключаются?
6. Как формулируются правила нечеткого вывода для случая одной входной переменной, для случая двух входных переменных?
Список литературы
1. Андрейчиков А.В., Андрейчикова О.Н. Интеллектуальные информационные системы. - М: Финансы и статистика, 2004.
2. Рутковская Д., Рутковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы: Пер. с. польск. И. Д. Рудинского. – М.: Горячая линия – Телеком, 2004.- 452 с.
3. Усков А. А. Интеллектуальные технологии управления. Искусственные нейронные сети и нечеткая логика. - М.: Горячая линия-Телеком, 2004 .- 143 с.








