Глава. Элементы вариационного исчисления
Основные понятия
Пусть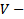 
ЛНП ( 
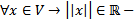норма
1) 
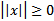,причем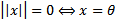 
2) 
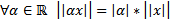
3) 
)
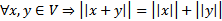Напомним, что функционалом называется правило(закон), по которому каждому элементу ЛП ставится в соответствие число.
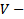вещественное ЛП
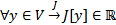
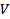считаем областью задания функционала
Замеч. Иногда функционал задан не на всем V, а на некотором его подмножестве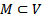 
. Тогда М считается областью задания функционала.
Основное ЛП, которое мы будем рассматривать, это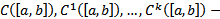 
ЛП функций, непрерывных на 
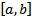со своими производными до к-го порядка включительно.
Норма в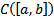 
вводится следующим образом :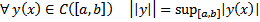 
В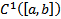 
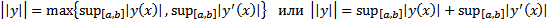
В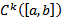 
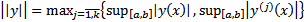или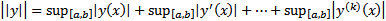 
Поскольку элементами рассматриваемой ЛНП являются фактически функции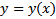 
, то мы их будем называть кривыми, а иногда точками, линейного пространства.
Опр.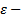 
окрестностью кривой 
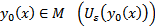называется совокупность всех кривых 
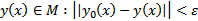. Если рассматривать 
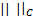, то окрестность называется сильной, а если это 
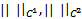и т.д. окрестность называется слабой
Опр.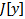 
называется непрерывной на кривой 
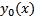, если 
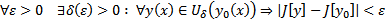(непрерывная тоже бывает слабая и сильная в зависимости от того, какая норма берется для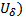 
Опр. Будем говорить, что функционал 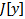достигает максимума на кривой 
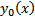, если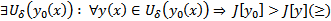 
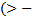строгий максимум, 
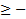нестрогий максимум) (так также может быть сильным или слабым, в зависимости от того, какая норма берется для 
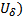. Аналогично определяется локальный минимум.
Локальный максимум или минимум будем называть локальным экстремумом функционала. Далее слово локальный будем опускать.
Замеч. Если функционал на кривой 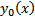достигает сильного экстремума, то он достигает и слабого, обратное неверно.
Всякое условие, необходимое для слабого экстремума, необходимо и для сильного. Это будем использовать в дальнейшем.
Опр. Если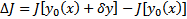 
можно представить в ви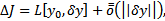де 
где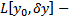 
линейный по 
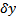функционал 
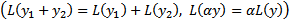, то 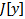называется дифференцируемым в точке 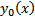, а 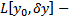его вариацией в точке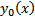
Опр. Пусть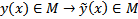 
Тогда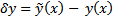 
называется вариацией кривой(т.е. вариация кривой это произвольное ее приращение)
Опр. Пусть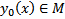 
. Рассмотрим 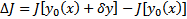. Эту разность назовем приращением функционала
Опр. Пусть число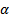 
достаточно мало, так что 
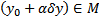. Тогда если 
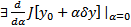, то она называется вариацией функционала 
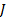в точке 
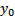(в узком смысле)
Можно показать, что если функционал является дифференцируемым в узком смысле, то он будет дифференцируем и в широком смысле, причем обе вариации при этом совпадают. Обратное, вообще говоря, неверно. Однако для интегральных, которые мы будем рассматривать, это одно и то же. Но вариация в узком смысле проще вычисляется, поэтому будем дальше пользоваться вторым(т.е. в узком смысле)
Теор. (Необходимое условие экстремума дифференцируемого функционала)
Если дифференцируемый функционал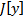 
достигает экстремума во внутренней точке 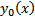множества М ( 
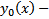внутренняя точка М, если 
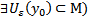, то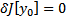 
Док-во: Пусть ради определенности на кривой 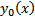достигается минимум 
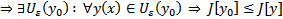. Возьмем произвольную ненулевую вариацию 
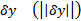. Рассмотрим всевозможные 
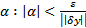. Тогда 
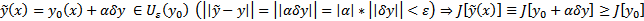. Рассмотри функцию одного переменного : 
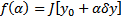. Тогда для тех же 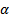выполняется, что 
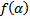достигает минимума в точке 
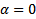, т.к. 
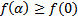. Поскольку 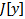дифференцируем в точке 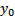, то 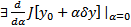, но эта производная будет равна 
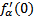. А в точке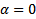 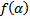достигает минимума 
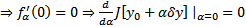, т.е. 
#
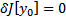Вопрос 39.