ТСЕ решение ЗК для уравнения 1-го порядка, разрешенного относительно производной. До-во существования решения
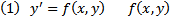определена в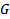 
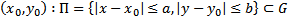
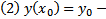начальные условия
ЗК. Найти интегральную кривую уравнения (1) проходящую через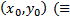 
найти решение (1), удовлетворяющее н.у. (2))
Теор. Пусть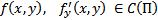 
. Тогда 
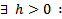в 
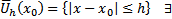решение уравнения (1) удовлетворяющее н.у. (2) и это решение единственное на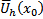 
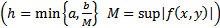
Док-во: Поэтапное доказательство существования решения
1) Докажем, что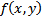 
удовлетворяет в П условию Липшица по переменной 
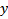, т.е. 
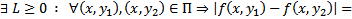теор. о конечных приращениях 
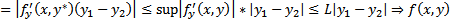удовлетворяет условию Л в П
2) Докажем, что ЗК (1), (2) эквивалентна интегральному уравнению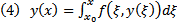 
## 
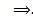Пусть 
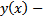решение ЗК (1), (2). Тогда 
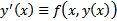. Проинтегрируем это тождество от 
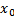до 
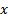
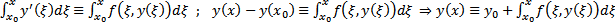
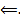Пусть 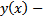решение (4). Тогда 
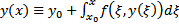Дифференцируем по 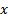, получим : 
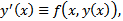причем 
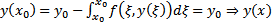является решением ЗК (1), (2)##
3) (Построение функциональной последовательности) Строим функциональную последовательность следующим образом. Везде считаем, что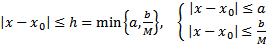 
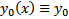
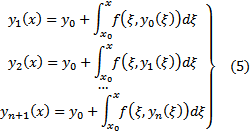
4) (Принадлежность П)
Покажем, что при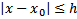 
выполняется, что 
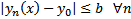т.е.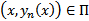 
## 
……
##
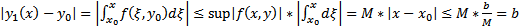
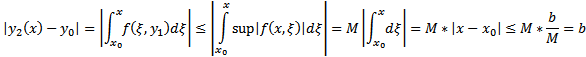
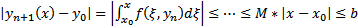5) (Абсолютная и равномерная сходимость функциональной последовательности)
Покажем, что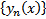 
сходится абсолютно и равномерно на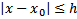
## Очевидно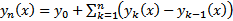 
Таким образом, сходимость последовательности 
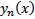эквивалента сходимости функционального ряда 
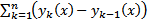(т.к.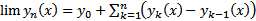 
Рассмотрим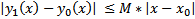 
. Тогда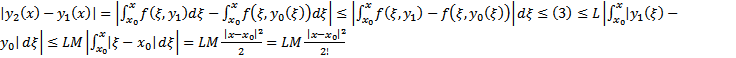 
……
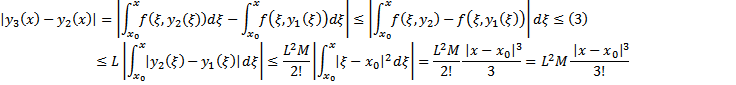
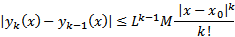
Тогда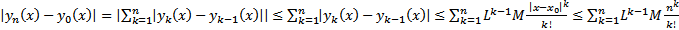 
Числовой ряд 
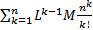Сходится по признаку Даламбера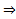 
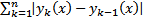мажорируется сход числовым рядом 
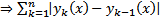сходится абсолютно и равномерно на 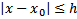по правилу Вейерштрассе. 
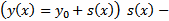сумма ряда. 
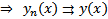причем 
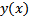непрерывна при 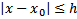в случае равномерной сходимости.
Замеч.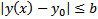 
в силу теоремы о предельном преходе в неравенствах
6) (Равномерная сходимость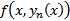 
)
Покажем, что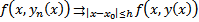 
## 
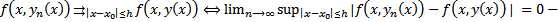критерий сходимости функциональной последовательности. Рассмотрим 
##
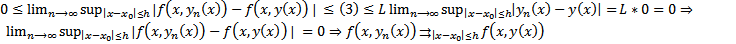7) (Решение интегрального уравнения)
Покажем, что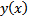 
является решением интегрального уравнения (4)
## 
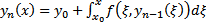(из (5)) 
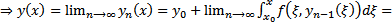в силу равномерной сходимости 
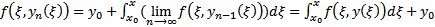Но поскольку интегрируемое уравнение (4) эквивалентно ЗК (1), (2) то 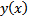и является решенной ЗК ##
Таким образом доказано, что решение ЗК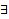 
Доказательство конструктивное. Указан метод построения решения. (Метод последовательного приближения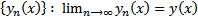 
#
Вопрос 37.
ТСЕ. Доказательство единственности.
Лемма. (Лемма Гронуолла)
Если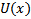 
непрерывна и неотрицательна на 
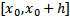и удовлетворяет условию 
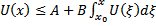, то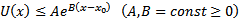 
Док-во: рассмотрим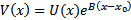 
, которая также непрерывна и неотрицательна на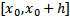 
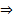достигает своей верхней грани на 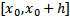. Предположим, что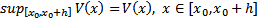 
#
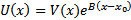
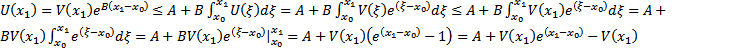
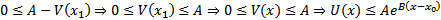Докажем теперь единственность решения ЗК на 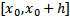(слева доказывается аналогично)
Док-во: Пусть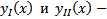 
решения ЗК на 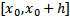. Тогда 
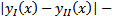непрерывно, неотрицательно на 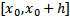и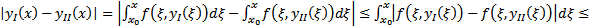 
условие Л в П 
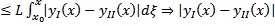удовлетворяет условию Леммы Гронуолла с 
#
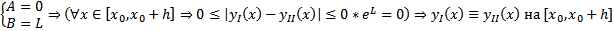Вариант 38.