Неоднородные ЛОДУ ВП. Метод вариации произвольных постоянных.

Дата: 2025-06-02; Просмотры: 15

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

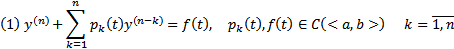
Теор. (Об общем решении НЛОДУ ВП)

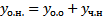
Док-во: Приведем (1) к виду (2)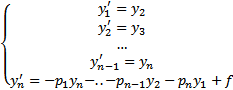

Пусть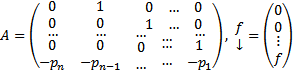

Получили неоднородное СЛОДУ 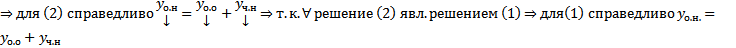. Покажем, что 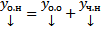справедливо для (2).

Покажем, что 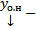решение. 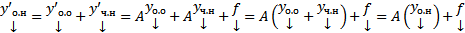. Покажем теперь, что любое решение СЛОДУ (1) входит в (3). Пусть 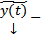произвольное решение (1). Рассмотрим разность 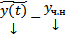. Покажем, что эта разность удовлетворяет (2). 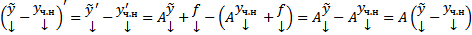. Пусть 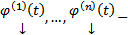какая-нибудь ФСР ОСЛОДУ (2), тогда 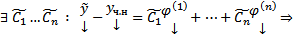любое решение 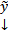СЛОДУ (1) может быть представлено в виде 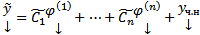при некоторых значениях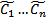

Вопрос 30.

Будем искать ч.н. методом вариации произвольных постоянных

Пусть 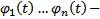произвольная ФСР ОЛОДУ. Тогда 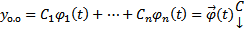, где 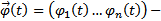строка элементов ФСР, 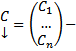столбец произвольных постоянных.

Будем искать 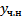в ви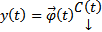де , где 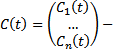столбец неизвестных пока функций. Тогда 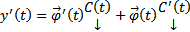, наложим условия, что 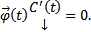Тогда

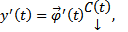
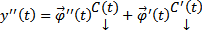, наложим условия 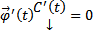. Тогда 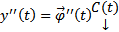и т.д. На каждом шаге полагаем, что .

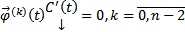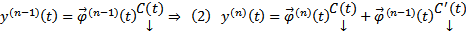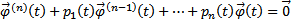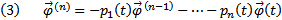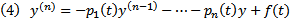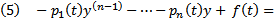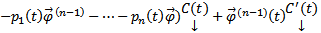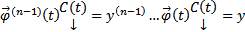Тогда Поскольку , тогда . С другой стороны, поскольку y является решением неоднородного уравнения (1), то Подставим (3) и (4) в (2) получим : ( , но Поэтому после сокращения в (5) : 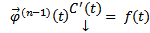Следовательно, столбец 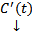удовлетворяет случ СЛАУ

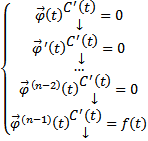Запишем в развернутой форме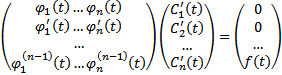

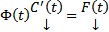Поскольку 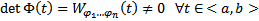, то 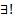решение 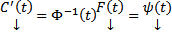Интегрируя, получаем :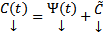

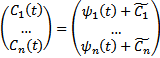Тогда (7) 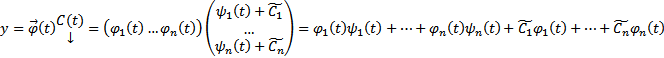Придавая константам 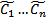произвольным значениям например, ноль 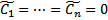, получим : 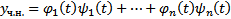Тогда (7) может быть представлено в виде 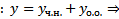это будет 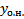. Таким образом, (7) дает при всевозможных 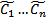общее решение неоднородного ОЛОДУ ВП.

Вопрос 31.

ГЛАВА. ЛОДУ ВП С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ

Однородные ЛОДУ ВП с постоянными коэффициентами

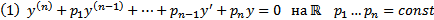
Рассмотрим ЛП 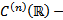ЛП функций, непрерывные с производной до n-го порядка включительно на 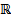. Пусть в это ЛП действ ЛО 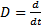, т.е.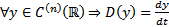

Далее получаем, что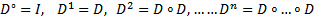

Тогда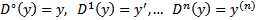

Рассмотрим многочлен n-ой степени : 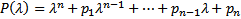Ему сопоставим ЛО 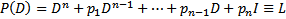Тогда (1) можно переписать в виде :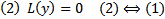

Будем искать решение (1) ( или что то же (2)) в виде 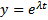. Подставим во (2)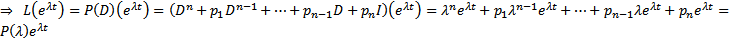

Видим, что 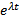будет решением (1) (или(2))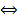 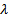является корнем уравнения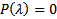

Опр. 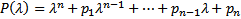называется характеристическим многочленом уравнения (1)( или (2)), а уравнение 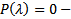характеристическим уравнением.

Теор. 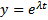является решением ОСЛОДУ ВП (1) ((2))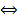 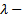корень характеристического уравнения

Док-во: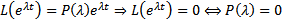

Способы построения ФСР

(А) Построение ФСР ОЛОДУ ВП в случае, когда все корни характеристического многочлена различны.

Пусть 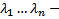различные корни характеристического многочлена. Тогда имеется n решений :

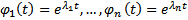Покажем, что они образуют ФСР, т.е. являются ЛНЗ

Док-во: Рассмотрим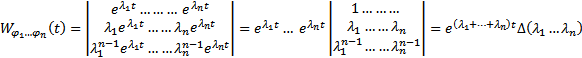

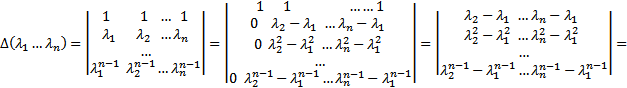далее из каждой строки начиная с последней вычитаем предыдущую строку умноженную на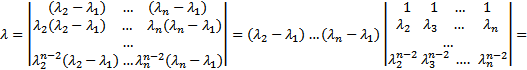

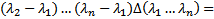по индукции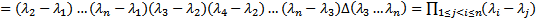

Отсюда видно, что если все 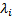различны, то 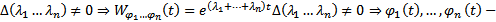ЛНЗ на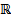 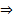ФСР

Вопрос 32.

(Б) Построение действительных ФСР для ОСЛОДУ ВП с действительными коэффициентами в случае простых корней характеристического уравнения при наличии комплексных

Замеч. ФСР, построенная в пункте (А) может быть как П-, так и 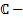значной. Если само уравнение имеет комплексные коэффициенты, то комплекснозначная ФСР дает произвольные комплекснозначное решение такого уравнения. Но допустим, что 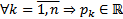и нас интересуют только вещественные решения. В этом случае, если среди корней характеристического уравнения имеются комплекные, мы имеем комплекснозначную ФСР и представление произвольного вещественного решения через нее затруднительно. Поэтому представляет интерес построение вещественной ФСР.

Пусть все корни характеристического уравнения различны, но имеются комплексные. Тогда если 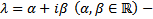корень характеристического уравнения, то 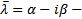тоже корень, поскольку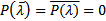

Упорядочим корни следующим образом :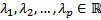

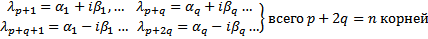
Соответственно комплексозначная ФСР будет :

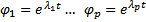
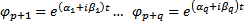
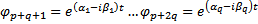
Тогда 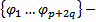базис в ЛП решений. Перейдем к системе функций :

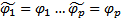
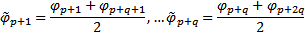
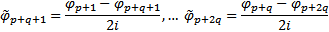
Матрица перехода 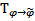будет иметь вид :

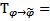
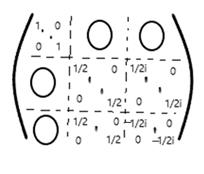
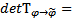
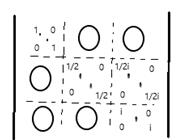
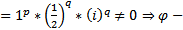ЛНЗ 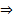базис

Но это будет уже вещественный базис, т.к. 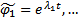, 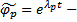вещественная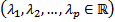

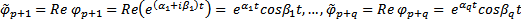
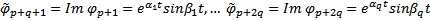
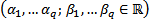
Вопрос 33.

(В) Случай кратных корней характеристического уравнения

Теор. Пусть 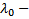корень кратности k характеристического уравнения, т.е.

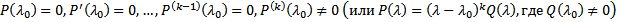. Тогда 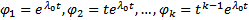является решением ОЛОДУ ВП 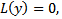отвечающим значению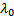

Перед доказательством этой теоремы рассмотрим.

Лемма. (Дифференциальное тождество)

Пусть 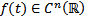. Тогда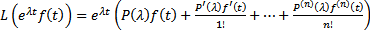

Док-во: Рассмотрим 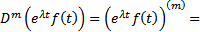формула Лейбница 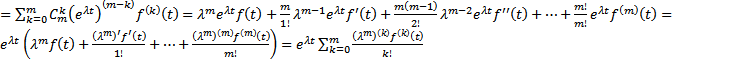. Тогда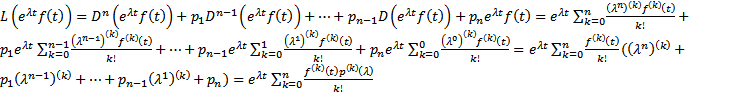

Докажем теперь теорему.

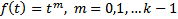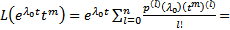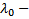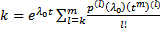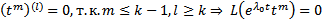Док-во: берем . Тогда поскольку корень кратности , но при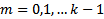

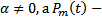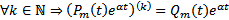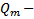Лемма. Если произвольный многочлен степени m, то , где многочлен той же степени.

Док-во: Методом математической индукции

БАЗА. 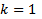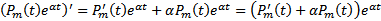Если 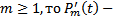многочлен степени (m-1), а 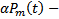многочлен степени m, в сумме будет многочлен степени m. Если же 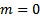, то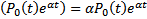

ШАГ. Пусть утверждение верно для 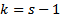, т.е. 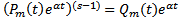Покажем, что тогда она верна и для 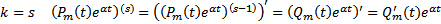(см базу) – верно 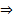утверждение верно #

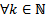Пусть теперь характеристическое уравнение имеет корни : 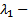кратности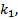 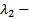кратности 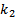,…, 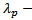кратности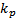 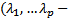различны, 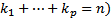. Тогда рассмотрим сумму h функций (решений ОЛОДУ ВП)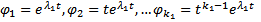

…

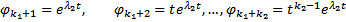
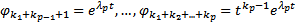Покажем, что эта система ЛНЗ (тогда это и будет ФСР). От противного. Предположим, что она ЛЗ, что 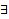нетривиальный набор чисел 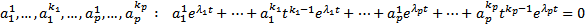. Поскольку набор чисел нетривиальный, то хотя бы один из многочленов 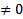. БОО считаем, что 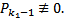На самом деле, не только он, т.к если бы все остальные многочлены 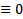, то мы бы получили тождество : 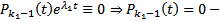противоречие 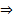есть еще какой-то ненулевой многочлен. Тогда 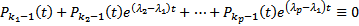Дифференцируем это тождество k раз 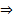по лемме 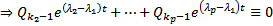Какой-то многочлен из 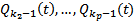будет 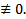БОО это 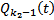. По тем же соображениям, что и выше не только он 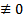, но и еще по крайней мере один другой. Умножаем обе части на 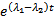, получим 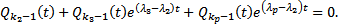Дифференцируем еще 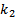раз. Далее используем те же соображения дойдем до того, что 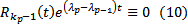. С одной стороны из рассуждений, приведенных выше, получаем, что 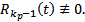С другой стороны тождество (10) может быть выполнено только при 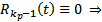противоречие. Оно возникло из предположения, что 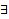нетривиальная ЛК построенных функций, которое 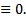Значит, предположение неверно 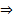только тривиальная ЛК 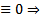построеная система функций ЛНЗ 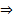она представляет собой ФСР (вообще говоря 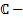значную). Для уравнения с вещественными коэффициентами из нее можно построить вещественную ФСР по тем же правилам что и в случае простых костей. #

Вопрос 34.

Неоднородные ЛОДУ ВП с постоянными коэффициентами.

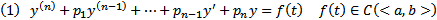
Напомним, что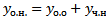

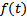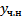В случае произвольной ищем методом вариации произвольных постоянных. Однако в случае специального вида 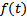удобнее применять метод неопределенных коэффициентов

Теор. (принцип суперпозиции)

Если 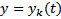является решением уравнения 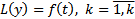, то 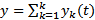является решением уравнения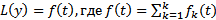

Док-во: #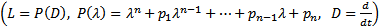

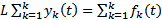Пусть 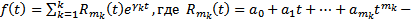многочлен степени 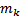с определенными коэффициентами, 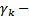произвольная(комплексная)

В силу принципа суперпозиции рассмотрим поиск 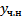для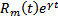

Возможны 2 случая :

1) 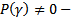нерезонансный случай

2) 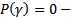резонансный случай

Нерезонансный случай

Пусть 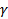не является корнем характеристического уравнения :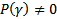

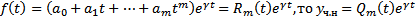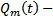Теор. Если . Где многочлен той же степени, что и 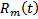, коэффициенты которого определяются единственным образом

Док-во: Подставим 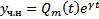в уравнение 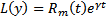используя диф тождество : 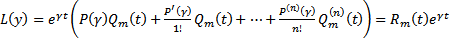. Тогда 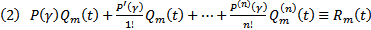Рассмотрим ЛО, действующую ЛП многочленов степени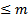 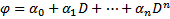Тогда (2) примет вид 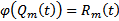. Покажем, что 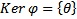т.е. ядро состоит только из многочлена 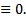От противного. Предположим, что 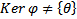. Тогда 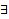многочлен 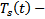многочлен степени s : 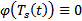. Но 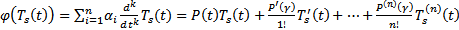. Тогда если s=0, т.е. 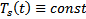, то первое слагаемое 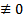, а остальные 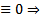невозмодно, чтобы 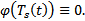Если же 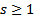, то первое слагаемое будет многочленом степени s , а остальные слагаемы е имеют степень <s 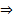невозможно, чтобы сумма 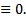Мы пришли к противоречию : 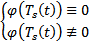Таким образом получаем, что 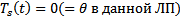. Таким образом 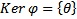. Тогда 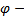обратим, т.е. 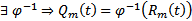, т.е. по заданному многочлену 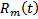многочлен 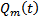определяется единственным образом

Замеч. На практике полагают, что 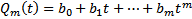, подставляем 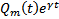в уравнение 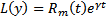, получают точку, сокращают обе части на 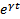и приравнивают коэффициенты при степени t , получа.т СЛАУ из 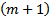уравнений с 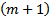неизвестными

Вопрос 35.

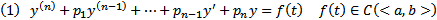
Напомним, что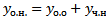

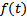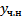В случае произвольной ищем методом вариации произвольных постоянных. Однако в случае специального вида 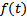удобнее применять метод неопределенных коэффициентов

Теор. (принцип суперпозиции)

Если 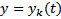является решением уравнения 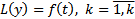, то 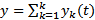является решением уравнения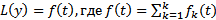

Док-во: #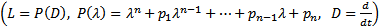

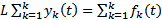Пусть 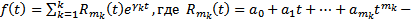многочлен степени 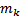с определенными коэффициентами, 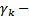произвольная(комплексная)

В силу принципа суперпозиции рассмотрим поиск 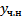для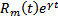

Возможны 2 случая :

1) 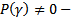нерезонансный случай

2) 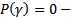резонансный случай

Резонансный случай.

Пусть 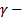корень характеристического уравнения кратности k :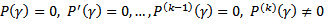

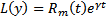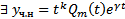Теор. Если , то , где 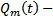многочлен той же степени, что и 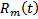и его коэффициенты по данным коэффициентам 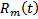определяются единственным образом.

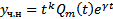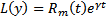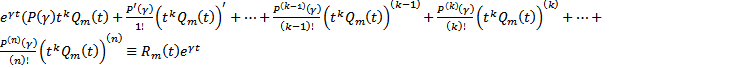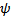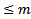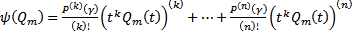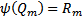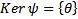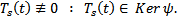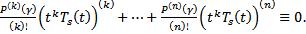Док-во: Используя диф тождество, подставим в уравнение , получим : . Рассмотрим ЛО , действующего в ЛП многочлена степени . . Тогда . Покажем, что . От противного. Пусть Тогда Если 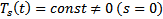, получим 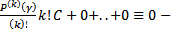невозможно. Если же 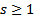, первое слагаемое многочлена степени s , а остальные слагаемые имеют степень < s, т.к. там берутся более высшие производные 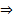невозможно чтобы сумма = 0. Пришли к противоречию 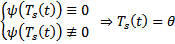, т.е. нулевой многочлен. Таким образом 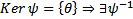Он определяется единственным образом. 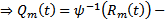определяется единственным образом

Замеч. На практике 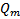отыскивают подставляя 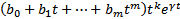в уравнение 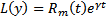, сокращая 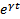и приравнивая коэффициенты при одинаковых степенях t. Получают СЛАУ из 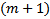неизвестных. Из док-ва теоремы получаем, что она имеет единственное решение.

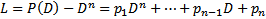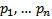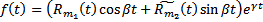Если уравнение имеет действительные коэффициенты , а , где 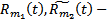многочлены степеней 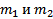с действительными коэффициентами, 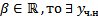в ви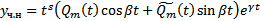де , где 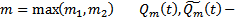многочлены степени m с действительными коэффициентами 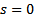, если 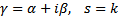, если 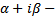корень кратности k

Вопрос 36.