Глава. Линейные системы с постоянными коэффициентами.
ФСР ОСЛОДУ с постоянными коэффициентами.
(1) 
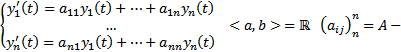постоянная матрица, т.е.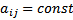 
Будем искать решение это системы в виде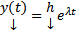 
Подставим в (1) получим :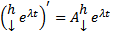 
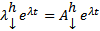Поскольку 
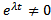, то 
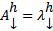. Если нас интересует нетривиальные решения, то 
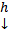должно быть нетривиальное решение ОСЛАУ (2) 
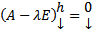квадр ОСЛАУ (2) имеет нетривиальные решения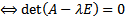 
Опр. Уравнение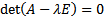 
называется характеристическим уравнением.
Известно, что в поле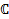 
оно имеет n корней с учетом их кратности.
Замеч. Фактически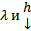 
являются соответственно СЗ и комп СВ ЛО, имеющего в некотором базисе матрицу А.
Получаем, что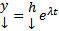 
является нетривиальным решением ОСЛООДУ (1)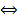 
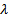является корнем характеристического уравнения, а 
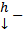соответственно СВ.
Построение ФСР ОСЛОДУ (1)
Все корни характеристического уравнения вещественны и различны. Т.е. имеем набор решений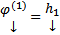 
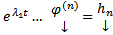
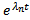
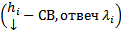. Поскольку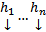 
отвечают различным С, то они ЛНЗ. Покажем, что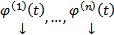 
образуют ФСР ОСЛОДУ (1), т.е. является ЛНЗ на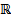 
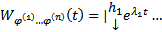
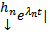
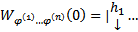
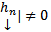т.к. в столбцах det записаны координаты ЛНЗ векторов 
. 
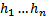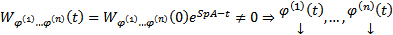ЛНЗ на всей 
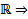это ФСР ОСЛОДУ (1)
Замеч. В рассматриваемом случае предполагалось, что А – вещественная матрица и была построена соответствующими вещ ФСР
Если А – комплексная матрица и все корни характеристического уравнения различны, то ФСР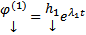 
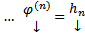
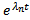будет комплекснозначной. Тогда всевозможные ЛК элементов этой ФСР с комплексными коэффициентами дадут всевозможные комплексные решения ОСЛОДУ (1)
Вопрос 21.
(1) 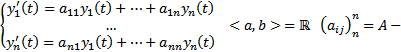постоянная матрица, т.е.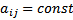
Будем искать решение это системы в виде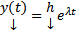
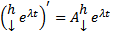
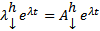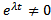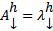Подставим в (1) получим : Поскольку , то . Если нас интересует нетривиальные решения, то 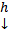должно быть нетривиальное решение ОСЛАУ (2) 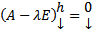квадр ОСЛАУ (2) имеет нетривиальные решения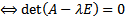
Опр. Уравнение 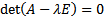называется характеристическим уравнением.
Известно, что в поле 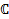оно имеет n корней с учетом их кратности.
Замеч. Фактически 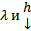являются соответственно СЗ и комп СВ ЛО, имеющего в некотором базисе матрицу А.
Получаем, что 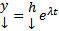является нетривиальным решением ОСЛОДУ (1)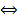 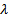является корнем характеристического уравнения, а 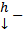соответственно СВ.
Построение ФСР ОСЛОДУ (1)
Пусть А - теперь действительная матрица, все корни характеристического уравнения простые, но среди них имеются комплексные. В этом случае комплексная ФСР строится точно так же, но если нам необходимы только всевозможные действительные решения ОСЛОДУ (1), то необходимо построить действительную ФСР и в этом случае.
Построение действительной ФСР в случае вещественной А, у которой все корни характеристического уравнения простые, но среди них имеются комплексные.
Пусть имеется p вещественных корне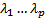й 
и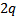 
комплексных корней 
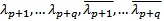(Если А – вещ и 
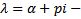корень характеристического уравнения, то 
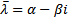также корень характеристического уравнения)
Док-во: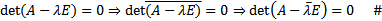 
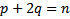Все корни различны. Рассмотрим комплексную ФСР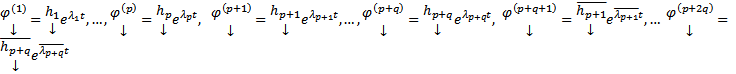 
= 
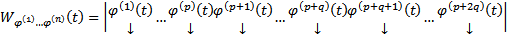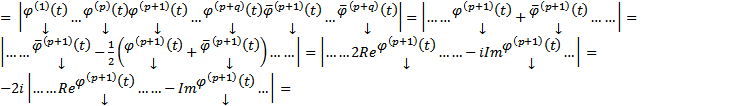те же действия производим с остальными переменными столбцов кс решений, тогда через q шагов получим 
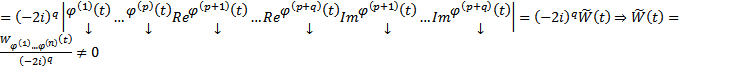Таким образом получим систему 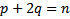ЛНЗ действительных решений. Это и будет действительная ФСР. Окончательно, действительная ФСР имеет вид 
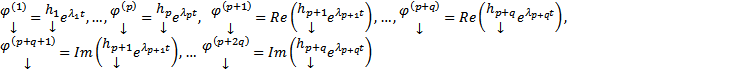т.е. в комплексной ФСР каждая пара 
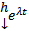и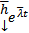 
нами заменена на пару (ЛНЗ)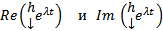 
Вопрос 22 .