Матрица решений и определитель Вронского.

Дата: 2025-06-02; Просмотры: 13
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Пусть 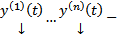произвольные решения (1) (или(3)). Запишем из по столбцам в матрицу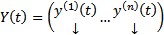

Опр. 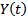называется матрицей п=решений ОСЛОДУ (1). Поскольку 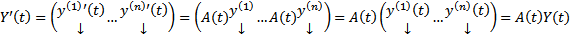, то матрица решений формально тоже удовлетворяет ОСЛОДУ (1), т.е.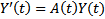

Опр. Матрица решений построена на ФСР ОСЛАДУ (1), т.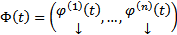е. , где 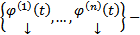произвольная ФСР ОСЛОДУ (1), назовем фундаментальной матрицей решений (ФМР)

Опр. Рассмотрим 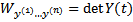. 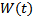назовем определителем Вронского (вронскианом) системы решений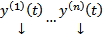

Замеч. определитель Вронского можно рассматривать для любой системы n столбцов функций высоты n 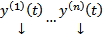, т.е. не обязательно для решений ОСЛОДУ.

Свойства МР и ОВ.

1) Пусть 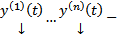ЛЗ на 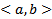системы столбцов функций высоты n (не обязательно решений ОСЛОДУ). Тогда 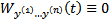на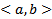

Док-во: Система ЛЗ 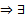нетривиальный набор 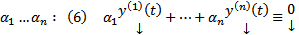на 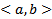. При любом фиксированном 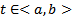(6) представляет собой ОСЛАУ относительно 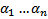.Поскольку 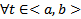у нее имеется нетривиальное решение, то 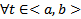определитель этой системы =0. Но определитель этой ОСЛАУ это 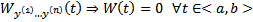, т.е.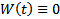

2) Пусть 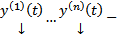система решений ОСЛОДУ (1) с непрерывными коэффициентами и 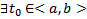: 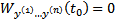. Тогд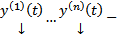а ЛЗ на 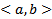( соот 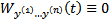на )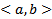

Док-во: Рассмотрим ОСЛАУ относительно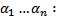

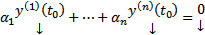
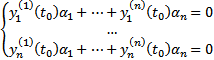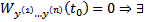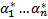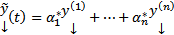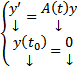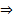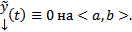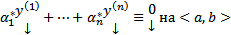Поскольку ее определитель есть нетривиальное решение. Пусть это . Рассмотрим тогда это ЛК решений ОСЛОДУ (1), т.е. тоже решение, причем оно является решением ЗК Но эта ЗК обладает тривиальным решением по ТСЕ Т.о. то 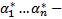нетривиальный набор 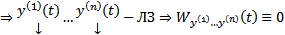на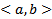

Замеч. Если 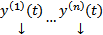не является решениями ОСЛОДУ (1) с непрерывными коэффициентами то это свойство не обязано выполнятся

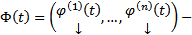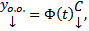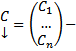3) Пусть ФМР для ОСЛОДУ (1) , то где столбец произвольных постоянных

Док-во: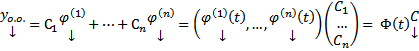

4) Если Ф(t) – ФМР ОСЛОДУ (1), то с непрерывными коэффициентами ЗК 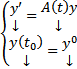имеет решение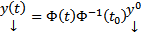

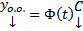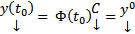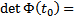
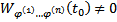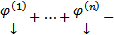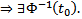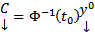Док-во: решению ЗК соответствует конкретный набор произвольных постоянных. Найдем его. Имеем Поскольку (т.к. ЛНЗ) Тогда Тогда решение ЗК есть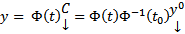

 

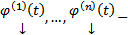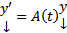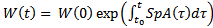5) Если ФСР ОСЛОДУ , то , где 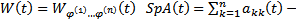след матрицы A(t)

Док-во: Докажем для n=2. Пусть 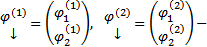ФСР ОСЛОДУ 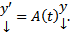Тогда k=1,2 получим, что (10)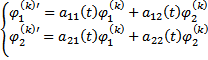 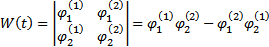. Тогда 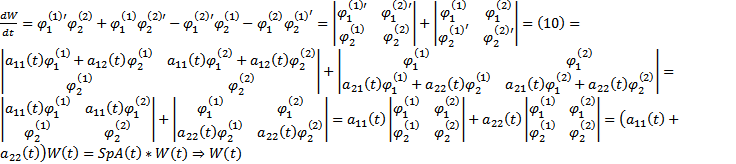удовлетворяет ОДУ

 

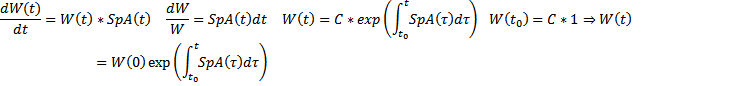
Вопрос 17

Построение ОСЛОДУ по заданной ФСР

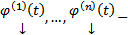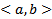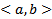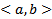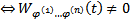Теор. Пусть система непрерывных дифференцируемых функций на . Тогда ОСЛОДУ с непрерывными на коэффициентами, для которой данный набор функций является ФСР на сущ. на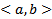

Док-во: 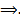Если 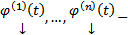ФСР некоторой ОСЛОДУ на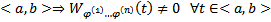

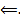Пусть 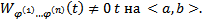Рассмотрим тогда следующую ОСЛОДУ.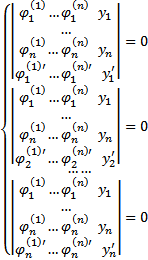

Каждый из столбцов 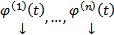удовлетворяет этой ОСЛОДУ. Раскроем теперь все определители по последнему столбцу, получим : 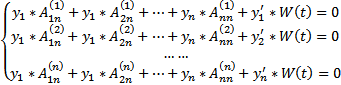Поскольку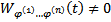 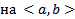, то получаем (11) 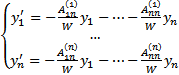это и есть ОСЛОДУ с непрерывными коэффициентами.

В процессе док-ва построена такая система для которой данный набор функции является ФСР системы.

 

Вопрос 18

Неоднородные СЛОДУ

(1)

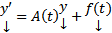
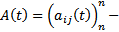непрерывные на 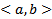коэффициенты 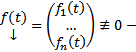правые части

Рассмотрим соответствующую ОСЛОДУ 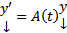(2)

Теор.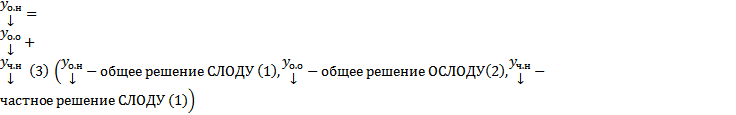

Док-во: Покажем, что 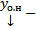решение. 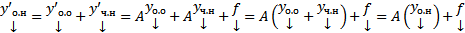. Покажем теперь, что любое решение СЛОДУ (1) входит в (3). Пусть 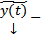произвольное решение (1). Рассмотрим разность 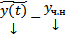. Покажем, что эта разность удовлетворяет (2). 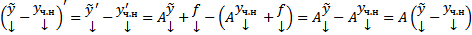. Пусть 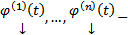какая-нибудь ФСР ОСЛОДУ (2), тогда 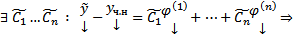любое решение 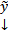СЛОДУ (1) может быть представлено в виде 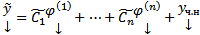при некоторых значениях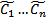

 

Вопрос 19

Метод вариации произвольных постоянных.

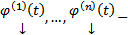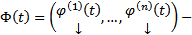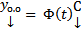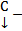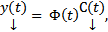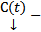Пусть ФСР ОСЛОДУ (1) ФМР. Тогда , где столбец произвольных постоянных. Будем искать решение неоднородной системы в виде (4) где столбец функций подлежащих определению. Подставим (4) в (1) : 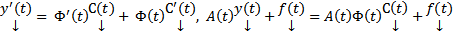, , 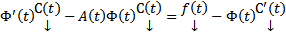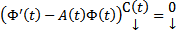т.к. ФМР является матричным решением ОСЛОДУ (2), т.е. 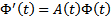. Тогда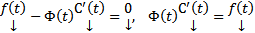

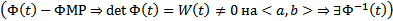
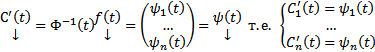. После интегрируем каждое из этих уравнений получаем : 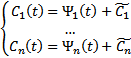где 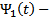первообразная 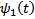… 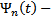первообразная 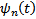, 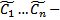константы. При каком-то конкретном наборе констант, например при 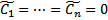получим, 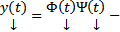будет некоторым частным решением. Если же оставить 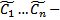произвольными, то получим 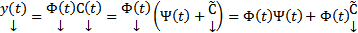. Тогда получим , т.е. все решения СЛОДУ (2)

 

Вопрос 20 .