Свойства решений ОСЛОДУ
1) (Тривиальность) ОСЛОДУ (1) всегда обладает решением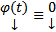 
Док-во: очевидно
2) (Линейность) Если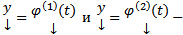 
некоторые решения (1), то 
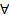чисел 
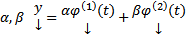также является решением (1)
Док-во: Введем в ЛП столбцов функций оператор L: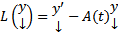 
, тогда систему (1) можно переписать в виде (3) 
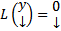. Пусть 
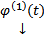и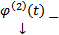 
решения, т.е. 
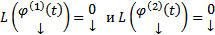. Тогда 
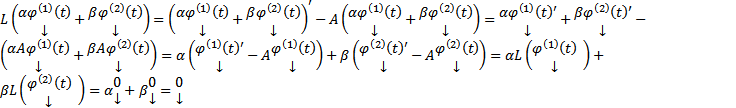. Сейчас доказано, что L является линейным оператором и что любая ЛК решения также является решением.
Замеч. Из 1) и 2) следует, что совокупность всевозможных решений ОСЛОДУ (1) образует ЛП, которое обозначим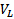 
3) (О нуле решения) Если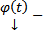 
решение (1) или (3) с непрерывными коэффициентами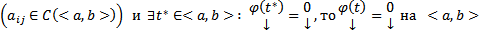 
Док-во: Рассмотрим ЗК для (1) :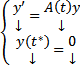 
С одной стороны 
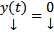является ее решением, с другой стороны 
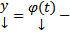тоже ее решение. Но по ТСЕ на всем 
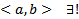Решение ЗК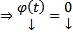 
4) (О линейной зависимости)
Пусть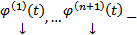 
решение (1) (или (3)) . Тогда эта система решения является ЛЗ
Док-во: Рассмотрим эту систему при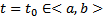 
. При фиксированном 
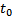это просто набор из 
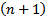столбца высоты 
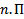оскольку ЛП столбцов чисел высоты 
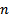имеет размерность 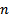, то система 
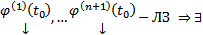нетривиальный набор 
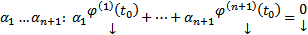(4). Рассмотрим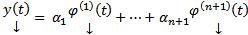 
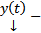ЛК решений (1) 
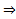является решением (2), причем 
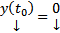в соответствии с (4). Таким образом 
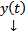является решением ЗК 
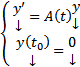, но эта ЗК также обладает решением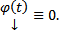 
По ТСЕ получаем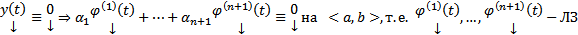 
5) (О линейной независимости)
ОСЛОДУ (1) (или (3)) с непрерывными коэффициентами обладает n ЛНЗ решениями
Док-во: Рассмотрим набор столбцов :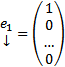 
, 
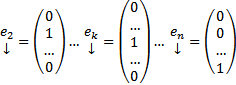и рассмотрим n штук ЗК : 
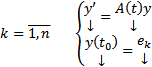где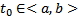 
. Пусть 
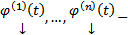решения этих ЗК соответственно. Предположим, что эта система решений ЛЗ. Тогда 
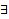нетривиальный набор 
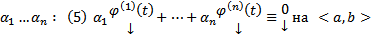. Тогда (5) должно быть выполнено и при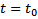 
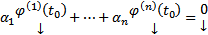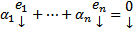т.е.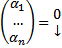 
т.е. 
т.е.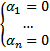 
. Противоречие тому, что набор 
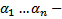нетривиально. Оно вызвано из предположения что 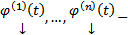ЛЗ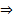 
эта система ЛНЗ на 
.
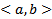Сл . Из 4 и 5 получаем, что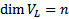 
(отсюда любой базис 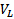содержит ровно 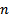элементов)
Вопрос 15.
(1) 
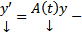ОСЛОДУ
(3)
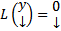
Опр. Любой базис в 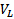назовем фундаментальной системой решений (ФСР) : ОСЛОДУ (1) (или(3)). Т.е. ФСР это упорядоченный набор из n ЛНЗ решений ОСЛОДУ (и всякое решение может быть передано как ЛК элементов этого набора)
6) (Об общем решении ОСЛОДУ)
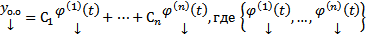назовем ФСР ОСЛОДУ, 
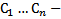произвольные постоянные
Док-во: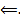 
Поскольку 
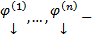базис, то любое решение является ЛК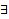 
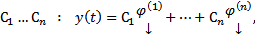
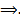Из свойства линейности любая ЛК 
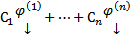является решением.
Вопрос 16 .
(1) 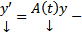ОСЛОДУ
(3)