Нормальные системы ОДУ 1-го порядка.
Рассмотрим (1)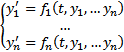 
Где t – независимая переменная, 
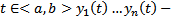неизвестные функции; 
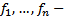заданные функции на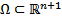 
Система ОДУ (1) называется нормальной системой ОДУ 1-го порядка(НСОДУ) с n неизвестными функциями. Само число n называется порядком системы.
Любое уравнение 1-го порядка, разрешенное относительно ст.производной :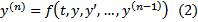 
можно свести к нормальной системе следующим образом:
Пусть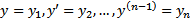 
, тогда получим нормальную систему, равносильную уравнению (2) : 
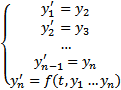(3)
Опр. Частным решением НСОДУ (1) называется совокупность дифференцируемых на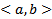 
функций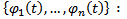 
1) 
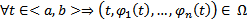
2) 
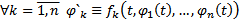на всем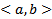
Опр. Совокупность всех частных решений НСОДУ (1) образуют общее решение
Ниже будет показано, что общее решение системы n-го порядка зависит от n произвольных постоянных.
Далее введем обозначение :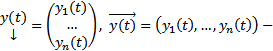 
столбец и строка неизвестных функций. 
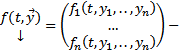столбец правых частей
В этих обозначениях (1) можно переписать в эквивалентном виде :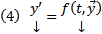 
. Тогда частное решение (4) это вектор столбец 
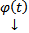(или вектор строка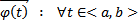 
1) 
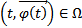
2) 
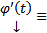
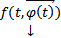
Пусть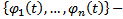 
какое-либо решение НСОДУ(1). По мере того, как t пробегает значения на 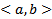, точка 
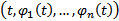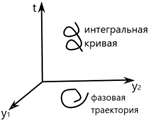
пробегает некоторую траекторию в 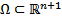она называется интегральной кривой НСОДУ (1)
n-мерное пространство переменных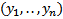 
назовем фазовым пространством , а проекцию интегральной кривой на фазовое пространство называется фазовой траекторией.
Поскольку НСОДУ (1) или (4) имеет бесконечно много решений (соответственно бесконечно много интегральных кривых), имеет смысл задача выделения интегральной кривой, удовлетворяющей некоторым дополнительным(начальным) условиям.
Опр. Задача нахождения НСОДУ(1)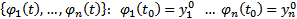 
(где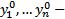 
набор начальных данных) называется ЗК для НСОДУ (1)
Коротко ЗК формулируется так :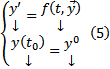 
Подразумевается, что 
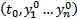является внутренней точкой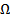 
Теор.(ТСЕ)
Пусть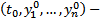 
внутренняя точка 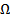и в некоторой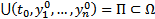 
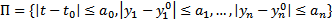выполняется, что
1) 
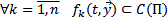
2) 
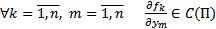Тогда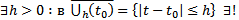 
решение ЗК (5)
Замеч. Если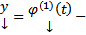 
решение ЗК (5) н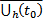а 
, а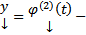 
решение ЗК (5) на некотором D, то 
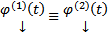на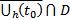 
Линейные нормальные системы.
Рассмотрим (1)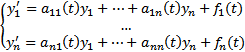 
Будем считать, что 
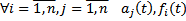определены и непрерывны на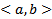
Опр. (1) называется линейной нормальной(СЛОДУ) системой (ОДУ 1-го порядка) (сама система имеет порядок n)
Введя обозначение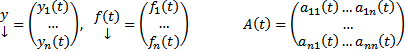 
перепишем (1) в виде 
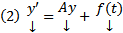. Если 
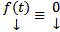(т.е. 
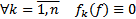на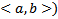 
, то СЛОДУ (1) (или (2)) называется однородной, в противном случае – неоднородной
Опр. ЗК для СЛОДУ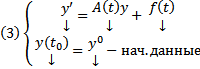 
Теор.(ТСЕ для СЛОДУ)
Если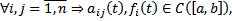 
то на всем 
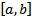при любом наборе начальных данных 
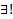решение ЗК (3) на всем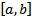
Без доказательства
Вопрос 13
(1) 
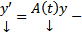ОСЛОДУ (3)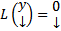 
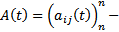матрица непрерывна на 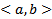функций (коэффициенты системы). Напомним, что в ЛП столбцов функций (высоты h) столбцы 
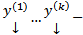называется ЛЗ, если 
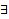нетривиальный набор чисел 
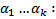(2) 
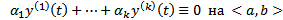. Если тождество (2) выполняется только при 
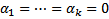, то система 
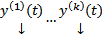ЛНЗ
Опр. Система столбцов называется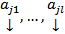 
линейно зависимой, если 
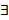нетривиальный набор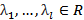 
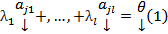. Если же (1) возможно только при 
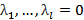, то система столбцов линейно независима.
Опр. Система строк называется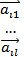 
линейно зависимой, если 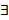нетривиальный набор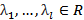 
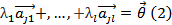. Если же (2) возможно только при 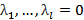, то система строк линейно независима.
Достаточные условия о ЛЗ и ЛНЗ:
1. Система столбцов, содержащая нулевой столбец, линейно зависимая
# ЛЗ и ЛНЗ сохраняются при любой нумерации столбцов, поэтому БОО можно считать что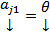 
,
тогда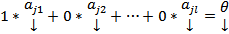 
=>это НТЛК =>ЛЗ #
2. Система столбцов, содержащая ЛЗ подсистему, ЛЗ
# БОО считаем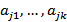 
линейно зависимая подсистема,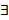 
: 
=> 
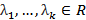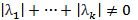
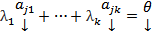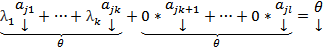это НТЛК => это ЛЗ#
3. Любая подсистема ЛНЗ системы столбцов является ЛНЗ
# Из предположения, что подсистема ЛЗ => система является ЛЗ, но по условию система столбцов является ЛНЗ => противоречие, значит подсистема ЛНЗ #
(Аналогично для системы строк)
Критерий ЛЗ
Система столбцов является ЛЗ ó один из них является линейной комбинацией остальных.
ð 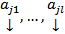- ЛЗ система столбцов, 
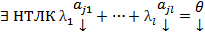, БОО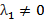 
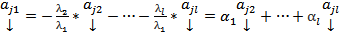, т.е. 
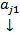- ЛК остальных
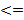Пусть один из столбцов ЛК остальных БОО считаем 
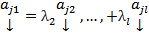Тогда
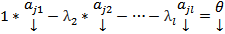- это НТЛК=> 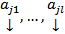линейно зависимая система
Вопрос 14 .
Однородные СЛОДУ.
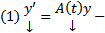ОСЛОДУ
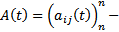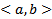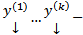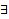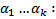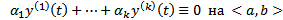матрица непрерывна на функций (коэффициенты системы). Напомним, что в ЛП столбцов функций (высоты h) столбцы называется ЛЗ, если нетривиальный набор чисел (2) . Если тождество (2) выполняется только при 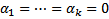, то система 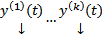ЛНЗ