Уравнения высших порядков, интегрируемые в квадратурах или допускающие понижения порядка.
Пусть 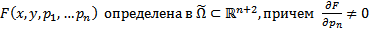
Опр. 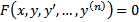 (1) называется ОДУ n-го порядка, не разрешенного относительно старшей производной.
(1) называется ОДУ n-го порядка, не разрешенного относительно старшей производной.
Допустим в некоторой области оно приводится к виду 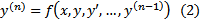 , где f определена в
, где f определена в 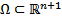 , то
, то
Опр. (2) называется ОДУ 1-го порядка, разрешенном относительно старшей производной
Опр. Частным решением уравнения (1) или (2) называется функция 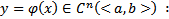
1) 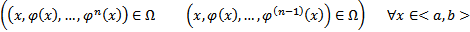
2) 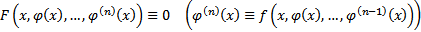 на
на 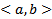
Совокупность всевозможных частных решений образует общее решение.
ЗК для (2) ставится следующим образом:
Нужно отыскать решения уравнения (2), удовлетворяющие дополнительному условию (называется начальными условиями)
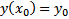
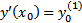
…
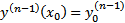
Т.е. 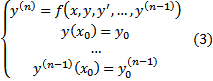
Теор. (ТСЕ решения ЗК (3) )
Если в некоторой области 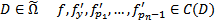 ,а точка
,а точка 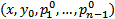 является внутренней точкой области D , то
является внутренней точкой области D , то 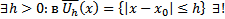 решение ЗК
решение ЗК 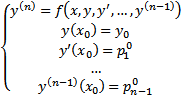
В области существования и единственности решения общее решение уравнения (2) зависит от n произвольных постоянных т.е. 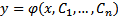 называется общим решением уравнения (2) если всякое частное решение (2) получено при некотором значении
называется общим решением уравнения (2) если всякое частное решение (2) получено при некотором значении 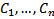 , а при любом наборе значений
, а при любом наборе значений 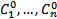
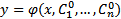 представляет собой решение (2). Если это решение задано в неявном виде
представляет собой решение (2). Если это решение задано в неявном виде 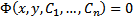 , то говорят об общем интеграле уравнения (2).
, то говорят об общем интеграле уравнения (2).
Соотношение вида 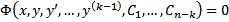 являющееся следствием уравнения (2), называется частным интегралом этого уравнения. Например, соотношение
являющееся следствием уравнения (2), называется частным интегралом этого уравнения. Например, соотношение 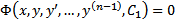 или
или 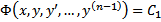 , является следствием уравнения (2), называется первым интегралом. Т.е. функция
, является следствием уравнения (2), называется первым интегралом. Т.е. функция 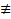 const, но сохраняет постоянное значение на любом решении уравнения (2)
const, но сохраняет постоянное значение на любом решении уравнения (2)
Вопрос 11
А) Простейшее уравнение n -го порядка
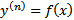 , где
, где 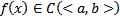 . Проинтегрировав это уравнение по x
. Проинтегрировав это уравнение по x 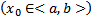
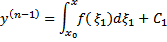
Далее 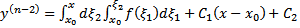
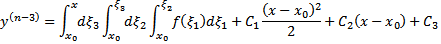
Через некоторое количество шагов
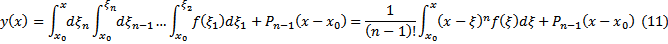
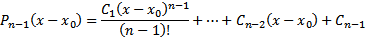
Док-во: Докажем (11) методом математической индукции.
БАЗА. 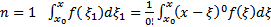 (верно)
(верно)
ШАГ. Пусть утверждение верно для 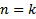 , т.е.
, т.е. 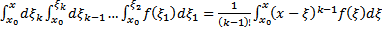 .
.
Тогда 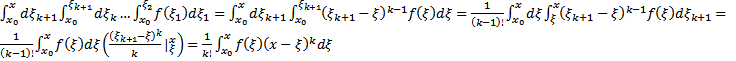 , т.е. формула верна и для
, т.е. формула верна и для 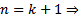 утверждение верно.
утверждение верно.
Таким образом, простейшее уравнение n-го порядка всегда интегрируемо в квадратурах имеет вид (11) #
Теперь докажем, что 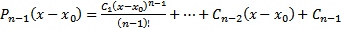
Док-во: Применим метод ММИ. БАЗА 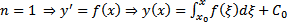 , т.е.
, т.е. 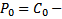 верно . ШАГ Пусть утверждение верно для
верно . ШАГ Пусть утверждение верно для 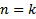 , то есть выполнено
, то есть выполнено 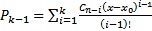 . Тогда
. Тогда 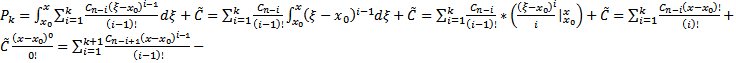 верно, то есть формула верна и для
верно, то есть формула верна и для 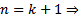 утверждение верно
утверждение верно 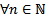 #
#
Таким образом, простейшее уравнение n-го порядка всегда интегрируется в квадратурах, и его решение имеет вид 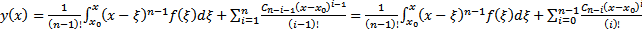
Б) Уравнения, допускающие понижения порядка
а) 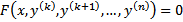 , то подстановкой
, то подстановкой 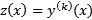 уравнение понижается на к единиц
уравнение понижается на к единиц 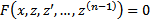 . Допустим, что решение
. Допустим, что решение 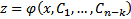 . Тогда полученный промежуточный интеграл
. Тогда полученный промежуточный интеграл 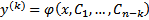
б) 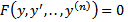 x не входит в уравнение в явном виде. Порядок уравнения можно понизить на единицу заменой переменных
x не входит в уравнение в явном виде. Порядок уравнения можно понизить на единицу заменой переменных 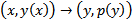 , где
, где 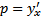 . Если
. Если 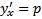 , то
, то 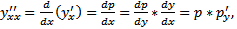
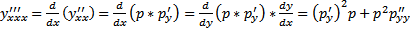 . Вообще
. Вообще 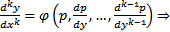 уравнение принимает вид
уравнение принимает вид 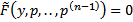 решаем уравнение и получаем
решаем уравнение и получаем 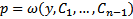 .
.
Далее решаем 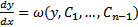
В) 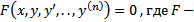 однородное, то аргумент
однородное, то аргумент 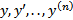 ,
,
т.е. 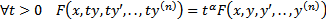 .
.
В этом порядок уравнения можно понизить на 1 заменой 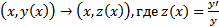 .
.
В этом случае 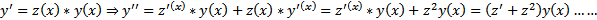
Докажем методом ММИ 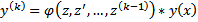
БАЗА для 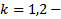 верно(см.выше)
верно(см.выше)
ШАГ индукции. Допустим, что утверждение верно для 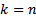 , докажем что оно также верно для
, докажем что оно также верно для 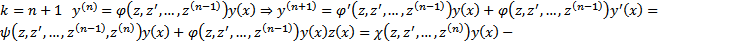 верно , то есть утверждение справедливо
верно , то есть утверждение справедливо 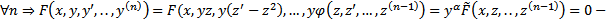 уравнение (n-1) порядка
уравнение (n-1) порядка
Г) Допустим, что 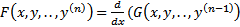 , тогда уравнение
, тогда уравнение 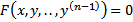 имеет первый интеграл
имеет первый интеграл 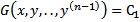 . Порядок снижается на 1.
. Порядок снижается на 1.
Вопрос 12 .








