Особые решения уравнения, не разрешенных относительно производных.
Рассмотрим (1)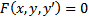 
Опр. Решение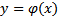 
называется особым решением уравнения (1) , если через любую его точку 
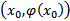по тому же направлению проходит другое решение уравнения (1) 
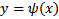, не совпадающее с 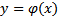в любой сколь угодно малой окрестности т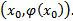 
Из этого определения следует, что если семейство решений имеет огибающую, то она является особым решением
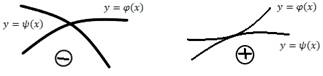
Как отыскать особые решения? Поскольку, в каждой точке особого решения нарушается единственность решения ЗК, то если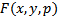 
является непрерывно дифференцируемой функцией нарушение единственности решения ЗК (в соответствии с ТСЕ) может возникнуть, если в некоторой точке 
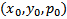выполняется это :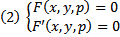 
Всякая кривая, являющаяся решением этой системы называется Р-дискриминантной кривой.
В частности, особое решение (если существует) является Р-дискриминантной кривой. Однако з-дискриминантная кривая не обязана является особым решением.
Вообще р-дискриминантная кривая может быть:
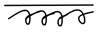Огибание
Точки заострения 
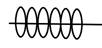
Точки прикосновения
Ассимптотич. 
Из всех этих случаев только огибающая является особым решением
Таким образом особое решение всегда непрерывно дифференцируема 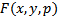ищем по схеме:
1) Отыскиваем всевозможные з-дискриминантные кривые (они являются решением системы (2))
2) Проверяем, являютcя ли эти кривые интегральными кривыми уравнения 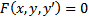(т.е. удовлетворяет ли ему)
3) Если они удовлетворяют этому уравнению, проверяем, нарушается ли в каждой их точке единственность решения , т.е.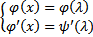 
Замеч. Это же касается с-дискриминантных кривых
Замеч. Если 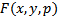не является дифференцируемым, то особое решение возможно определяется условием, что частные производные функции или сама функция неограничены.
Вопрос 9
Уравнение Лагранжа и уравнение Клеро
Опр. Уравнени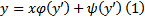е 
, где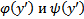 
непрерывные и дифференцируемые функции своего аргумента на некотором интервале , причем 
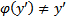, наз. уравнением Лагранжа. Применим к его решению метод введения параметра :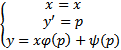 
Поскольку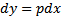 
С другой стороны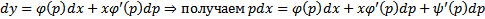 
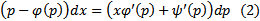Тогда уравнение (2) имеет решение 
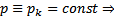уравнение Лагранжа (1) обладает решением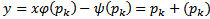 
Далее приведем (2) к виду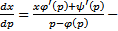 
это линейное неоднородное уравнение относительно 
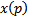. Оно всегда интегрируемо в квадратурах. Пусть его общее решение 
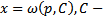произвольная постоянная. Тогда в параметрической форме решение уравнения Лагранжа задается следующим образом 
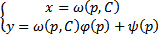Итого всевозможные решения уравнения Лагранжа (общее решение) будет :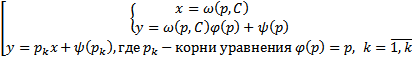 
Пусть теперь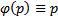 
, т.е. рассмотрим уравнение (3)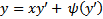 
Опр. Уравнение (3) называется уравнением Клеро
Решим его методом введения параметра. Имеем :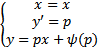 
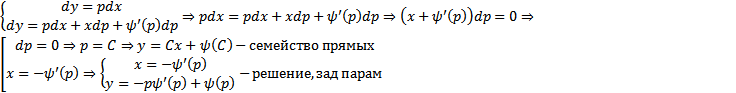
Таким образом, всевозможные решения уравнения Клеро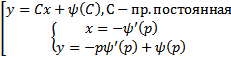 
Как соотносятся эти решения? Можно показать, что кривая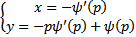 
являются огибающей семейство прямых 
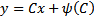, если 
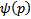не является линейной функцией.
Вопрос 10