Метод введения параметра
Рассмотрим уравнение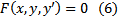 
Известно, что уравнение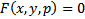 
задает некоторую поверхность в 
. Эта поверхность может быть параметризована следующим образом 
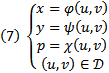причем для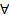 
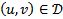выполняется 
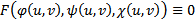. На каждом решении уравнения (6) должно быть выполнено соотношение 
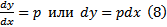. Из (7) и (8) получаем , что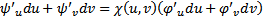 
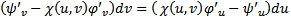
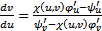а это уравнение для 
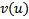, разрешенное относительно производной
Пусть его общее решение имеет вид :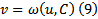 
т.е. на всякой интегральной кривой 
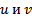связаны соотношением (9) при некотором значении С. Тогда общее решение исходного уравнения может быть параметрически задано следующим образом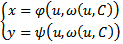 
Частный случай
Если уравнение (6) легко разрешить относительно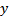 
т.е. представить в виде 
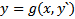, то в качестве параметров выбирают 
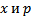по следующей схеме 
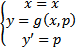Тогда 
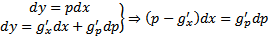
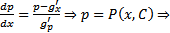общее решение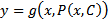 
общее решение задано неявно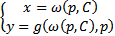 
, где р – параметр
Замеч. Нельзя писать далее, что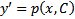 
и интегр его, т.к. р – параметр
Рассмотрим 
Самый простой случай решения уравнения – разрешить его относительно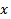 
, то есть привести к одному или нескольким уравнениям вида 
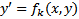и решить их, объединить все решения.Поскольку далеко не всегда удается это сделать , чаще применяется метод введения параметра.
Вопрос 8
Опр. Огибающей S семейство кривых называется линия, которая в каждой своей точке касается некоторой кривой(прямой) этого семейства, не совпадая с S в сколь угодно малой окрестности этой точки.
Рассмотрим уравнение Клеро
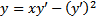
Решим его: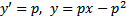 
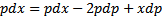
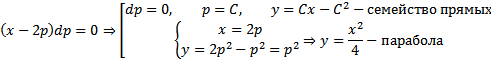
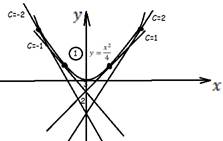Из курса дифф геометрии известно, что если семейство кривых
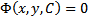имеет огибающую, то она является решением системы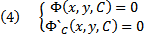 
Исключим С из этой системы, получим связь типа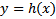 
. при этом всякая кривая 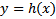задаваемая этой системой называется С-дискриминантной кривой. В частности, огибающая является С-дискриминантной кривой, но не только она.
С- дискриминантная кривая может содержать: огибание, точки заострения, узловые точки.
Огибание
Точки заострения(возврата)
Узловые точки
Но если известно, что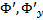 
ограничены и необратимы в ноль одновременно, то система (4) задает именно огибающую.
Поставим ЗК для уравнения Клеро
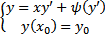
На нашем примере можно увидеть, что ЗК
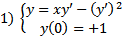
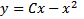
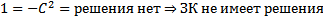
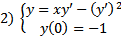
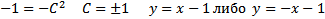По каждому из направлений 
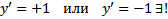Решение ЗК
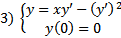Более одного решения проходит через точку (0;0) по заданному направлению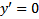 
По крайней мере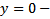 
решение и 
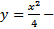решение, т.е. в случае 3) происходит нарушение единственности решения ЗК
Опр. Множество точек, в которых нарушается единственность решения ЗК называется особым множеством. Если это особое множество представляет собой интегр. кривую исходного ДУ, не разрешенного относительно производных, то говорят об особом решении. В частности, огибающая уравнение Клеро является особым решением этого уравнения.