Интегрирующий множитель
Пусть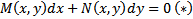 
не является УПД
Опр. Если существует дифференцируемая функция для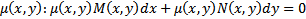 
становится УПД, 
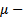называется интегрирующий множителем уравнения (*)
Каким условием должна удовлетворять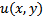 
В одной области
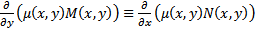или 
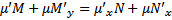, т.е. 
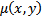должна удовлетворять уравнению в частных производных 
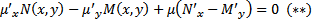. В общем случае это уравнение решить еще труднее чем исходное (*). Известно, что при непрерывном дифференцировании 
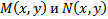не обращ в ноль одновременно, инт. множитель уравнения (*) существует.
Их существует 
много(инт. множество), а для того, чтобы решить уравнение, достаточно одной такой функции. Покажем, при каких условиях уравнение (*) имеет интегрирующий множитель специального вида, например
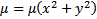. Обозначение: 
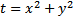. Тогда 
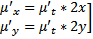подставим в (**), получим :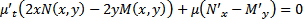 
(***) 
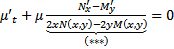
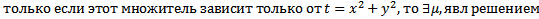ОДУ
Рассмотрим некоторые частные случаи, когда интегрирующий множитель легко находится.
Пусть 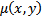не зависит от y, т.е. 
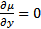. Тогда инт. мн-ль находится из ур-я: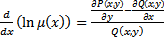 
Пусть 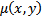не зависит от x, т.е. 
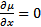. Тогда инт. мн-ль находится из ур-я: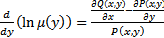 
Пусть P(x,y) и Q(x,y) – однор. ф-ии порядка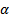 
. Введем 
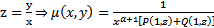, где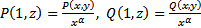 
Вопрос 6.
Уравнения 1-го порядка, не разрешенные относительно производной
Пусть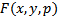 
определена в 
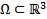. Рассмотрим уравнение 
.
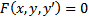Пусть уравнение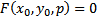 
имеет хотя бы одно решение 
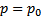, т.е.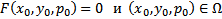 
Теор. (ТСЕ решения ЗК для уравнения 1-го порядка не разрешённого относительно производной)
Рассмотрим ЗК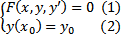 
1) 
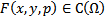
2) 
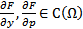
3) 
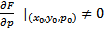тогда в некоторой 
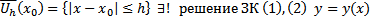, причем дополнительно выполнено условие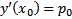 
Док-во: Из условий 1-3 получаем, что уравнение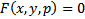 
задает в некоторой окрестности точки 
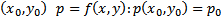(по ТСЕ неявной функции) 
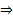ЗК приобретает вид 
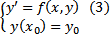, причем 
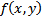непрерывна и 
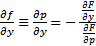непрерывна в окрестности точки 
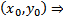выполняется условие ТСЕ решения ЗК для уравнения 1-го порядка, разрешенного относительно производной
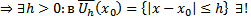решение ЗК (3), которое является и единственным решением ЗК (1), (2) удовлетворяющее дополнительному условию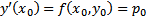 
Замеч. Дополнительная информация о решении 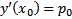необходима для того, чтобы из множества интегральных кривых, проходящий через 
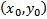выбрать кривую единственную проходящую по направлению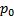 
может иметь несколько решений 
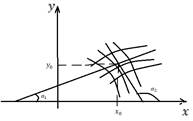Рисунок для случая, когда имеется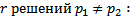 
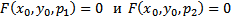. Каждая из ЗК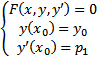 
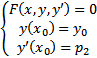имеет единственное решение
Замеч. Нарушение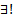 
решение ЗК, проходящего по заданному направлению чаще всего связанно с нарушением 3 свойства ТСЕ, т.е. если 
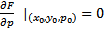. В этом случае ЗК может не иметь решения, а может и иметь, причем возможно неединственное, проходящее по этому направлению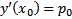
Маленькое дополнение
Допустим, имеется уравнение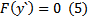 
Покажем, что в случае когда уравнение 
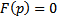имеет по крайней мере один действительный корень, общий интеграл (5) будет 
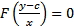(6)
Док-во: Пусть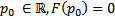 
, тогда 
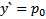задает решение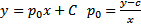 
Рассмотрим выражение 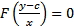. Покажем, что оно неявно задает 
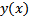является решением (5) , т.е. обратим его тождество при подстановке. По теореме о неявной функции, задается уравнение (6)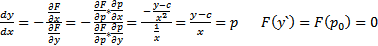 
Вопрос 7.