Загадка запрещения деления на ноль

Дата: 2025-06-15; Просмотры: 1

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Загадка запрещения деления на ноль

(Ликбез для рабочих: действия с нулём; разоблачение математического жульничества с нулём)

Если две качественно различные «вещ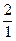и» и 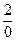порознь равны третьей, 2, то они равны между собой. Следовательно, .

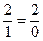Данный вывод кажется невероятным, хотя и является полученным на основе логического закона.

Теперь. Если наши предпосылки верны, если мы к ним правильно применяем законы мышления, то и результат должен соответствовать действительности. Посмотрим, поэтому, как у нас дело обстоит на практике.

Спросим себя, каким будет результат, если некое число m – а в нашем случае это – число 2 – сократить (разделить) количеством величиной в единицу, 1? Произведя расчет, получим, что сокращаемое (делимое) число окажется не сокращённым (не разделенным). Каким оно было перед началом сокращения (деления), таким оно и остается в итоге, m = m: 2 = 2. И точно так же 1 = 1, 0 = 0. Отсюда следует, что если равное количество сократить (разделить) на равное количество, то итогом будет величина, равная единице. Следовательно, далее, сама единица содержит в себе имманентное неистребимое противоречие: она есть и определенное количество, число 1, и отношение равных величин, 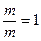, а именно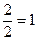, или 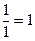, или , или 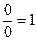, или и т.д.

А каким будет итог, если мы, напр., число 2 сократим (разделим) в 0 раз? По своему смыслу эта операция сводится к ничего не деланию в отношении числа 2. А если сделать попытку? Правильно. Итог будет тем же, что и в предыдущем случае, 2 = 2. Следовательно, в данном случае по своему эффекту в качестве делителей как 0, так и 1 качественно равны между собой: 1 = 0. Последнее равенство является, разумеется, не количественным, а качественным, в силу нулевого эффекта действия чисел 0 и 1 в качестве делителей числа 2; оно есть действительное противоречие, не устранимое по свое природе, и возникает всякий раз в аналогичных ситуациях. И в самом деле, сократим ли мы исходное число 2 в 1 раз или в 0 раз, результат будет одним и тем же, число не станет сокращенным (не станет разделенным), останется равным самому себе, 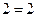. Стало быть и на деле[1]: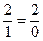

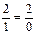Теперь становится видно, что тот результат, который был получен логически из на первый взгляд странных предпосылок, у нас совпадает с практическим результатом. А стало быть и наши изначально взятые теоретические предпосылки верны. И что, следовательно, так как две качественно различные «вещи», , равны между собой, то они равны чему-то третьему, которое само по себе есть, но не является ни первой, ни второй из них. И в нашем случае это – число 2.

Из фактического отношения равенства 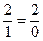, основой которого является абсолютное количественное совпадение, равенство исходного пункта и конечного результа, 2 = 2, равенство, полученное в итоге диаметрально противоположными способами, из этого фактического равенства 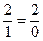вовсе не вытекает чисто количественное равенство: 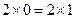. Такая нелепица может получиться только у того, кто из-за абстрактного, чисто количественного рассмотрения забывает о качественных различиях. И на деле последнее отношение не может вытекать из первого. В последнем случае 0 и 1 играют качественно иную роль, чем в первом случае, а именно, роль не делителей, а роль множителей. А в своей функции множителей числа 1 и 0 качественно не равны друг другу, перестают быть тождественными друг другу.

Кто станет отрицать, что если мы некую величину попытаемся умножить в ноль раз, то она не станет умноженной? Тоже самое касается и умножения на 1. И всё же число ноль в отличие от единицы по своей природе есть особенное число; оно по своему происхождению является невычисляемой конечной разностью равного, разностью, зафиксированной по общечеловеческому соглашению в положительной форме особого числа, 0. Это составляет имманентное противоречие нуля, быть одновременно и числом, и разностью чисел. Поэтому его природа может быть выражена, напр., таким образом: 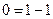, и это потому, что 1 = 1.

Ноль, взятый в функции множителя, он, аналогично единице, действительно не умножает никакого числа. Но в отличие от единицы он, наоборот, взятый в функции множителя в форме невычисляемой конечной разности равного раскрывает свою истинную сущность истребителя всякой величины и всякое число уничтожает, как истинный левеллер превращает его в себе количественно равное. Взятый же в функции делителя, ноль, хотя и позволяет раскрывать свою природу в адекватной ей форме невычисляемой конечной разности равного, заменять свою положительную форму, 0, отрицательной, (1 – 1), но бессилен точно также, как и взятая в этой же функции единца. Это – то внутреннее неистребимое противоречие нуля, в которое он впадает, когда его используют, начиная с уровня умножения и деления и выше в силу своей внутренне противоречивой природы. Здесь, как и везде, требуется не затушёвывать, скрывать, прятать неистребимые естественные противоречия, но разрешаемые по своей природе, а затем жульничать с ними, а выявлять и фиксировать их и учиться ими пользоваться, учиться ставить и разрешать их адекватно их природе для достижения правильных, адекватных же природе результатов.

Равенство 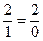в силу разрешения содержащегося в нём действительного, реально существующего противоречия, 1 = 0, при превращении 0 и 1 из делителей в множители – как это объяснено выше – и, благодаря этому, при установлении нового противоречия, в действительности превращается не в нелепое равенство 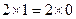, а распадается подобно распадению органической клетки – а это и означает установление нового противоречия – на два внешне самостоятельных, но внутренне связанных друг с другом (вот о каком новом противоречии идет речь!) и полярно противоположных, а потому и взаимопревращающихся друг в друга чисто количественных равенства:

.

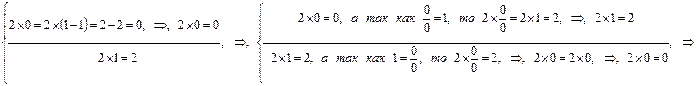
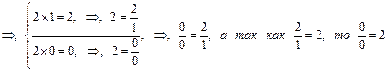
Из представленного движения вновь установленного противоречия путем разрешения предыдущего становится видно, что разрешение этого нового противоречия осуществляется путем параллельного и внешне независимого друг от друга превращения полярных крайностей друг в друга, что является доказательством их внутренней связи и единства при внешней кажущейся самостоятельности. Итогом процесса разрешения этого противоречия, как видно из примера путем превращения 0 и 1 из множителей вновь в делители, является установление качественно нового выражения и противоречия: 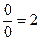. Это – результат отрицания отрицания.

Подытожим. Мы исходили из равенства 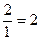. Подвергнув вышеприведенным способом его отрицанию, результатом этого мы получили равенство 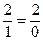, равенство, которое в наших руках в свою очередь практически и автоматически подверглось отрицанию рассмотренным способом, способом превращения 0 и 1 из множителей вновь в делители, с установлением в качестве результата этого отрицания отрицания равенства 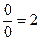. Этим процессом продемонстрировано здесь также происхождение отношения 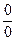, как идеального отражения реально существующей количественной связи мира, в котором мы живём.

Теперь. заглянем чуть-чуть вперед. Мы видели, что единица есть также и отношение равных величин. Поэтому и, напр., 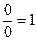. Однако, мы в итоге нашего исследования, подчинясь внутреннему закону его развития, закону отрицания отрицания, пришли к тому результату, что 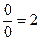. Следовательно, ограничиваясь только этими результатами, можно ли безусловно утверждать, что 2 = 1?! Здесь очевидно, ведь число 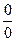есть всё таки нечто «иррационально» иное, чем число 2.

Не будем спешить, а посмотрим, в чем здесь состоит затруднение?

С самого начала нашего повествования исходным числом, над которым мы до сих пор проводили математические операции, было число 2. Что бы мы не делали посредством чисел 0 и 1 с числом 2, какие бы отношения у нас не возникали, не фиксировались и не изменялись, число два все это время оставалось по своему содержанию тем же самым вплоть до того момента, когда оно получило в наших руках выражение 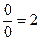. Но если бы мы исходно взяли не число 2, а, напр., число 3, то в результате бы получили, что 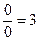. Если бы взяли число 5, то итогом было бы 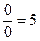. Если бы взяли любое число, m, то итогом бы было 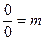. Таким образом, становится очевидным, что отношение 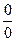способно выражать или иметь своим эквивалентом любое число, m, 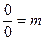, а именно, или = 1, или = 2, или = 3, или = 5, или = и т.д., следовательно, отношение 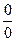для каждого случая, для определенных условий имеет соответствующее им значение. Отсюда на первый взгляд удивительное выражение 2 = 1 перед нашими глазами разворачивается в следующий бесконечно удивляющий бесконечный ряд: 2 = 1 = 3 = 5 = т.д. вплоть до = m.

Что выражается этим рядом, а в особенности последним членом этого ряда, а именно, m? То, что как число 2, так и число 1, так и и т.д., а в особенности так и число m есть определенное число, рассматриваемое безотносительно к его количественной определенности. Этим рядом выражается природа всех этих чисел, их внутреннее единство, то, что они все суть число, определенное количество, безотносительно к его количественной определенности, m. Лишь будучи выражением этого качественного равенства, формой выражения своего внутреннего единства, числа, этого числа, обозначенного нами буквой m, все они, эти 1, 2, 3 и т.д., могуть быть соизмеримыми, а стало быть и количественно различными, а именно, такими как и выглядят: 1, 2, 3 и т.д.. Поэтому выражение 2 = 1, как оно было получено выше, имеет смысл выражения 2 = m, где 1 есть лишь только внешняя форма существования этого m, и есть не количественное выражение, а качественное, выражение единого «субстрата» числа 2 в телесности числа 1 безотносительно к его величине, будто в числе m, в числе 1, уподобляющегося своими телесным свойствами телесности m, как противоречивом однобоком олицетворении числа m вообще, числа m, которе имеет столько же более или менее похожих или не похожих на себя своей внешностью олицетворений, сколько может быть цифр. Число вообще свое содержание в себе самом раскрыть не может, но только в чем-то другом, и, как мы видим, оно не выразимо абсолютно, но выразимо только относительно, в другом числе, напр., 2 = m, а, следовательно, m = 2. А потому у безличного числа, для которого мы взяли обозначение m, хотя могли бы взять n, имеется бесконечное количество лиц и ни одно из них не является адекватным. Такова вообще вся природа.

Отсюда, отношение 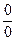выражает безразмерную, неопределенную величину вообще. А, стало быть, если в одном случае мы получаем 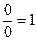, в другом случае получаем 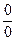= 2 , в третьем случае – 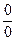= 5 , а в последнем случае полчаем 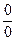= m , то итогом будет тот вывод, что отношение 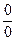или = 1, или = 2, или = 5, или = m в зависимости от особенностей условий каждого разбираемого случая. Отношение 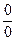есть действительное противоречие, состоящее в том, что оно есть отношение чистых количеств безотносительно к их количественной определённости. И это противоречие, еще раз, является только формой выражения безразмерного количества, абсолютно не имеющего ни какого эквивалента и абсолютно невыразимого. Такова вообще хитрость природы.

***

Теперь, зададим здесь себе вопрос, верно ли выражение 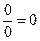? Является ли 0 числом, как сомневаются некоторые, и может ли оно быть присовокуплено к вышеполученному качественному ряду 2 = 1 = 3 = и т.д. = m?

1)

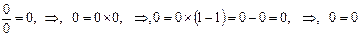
2)

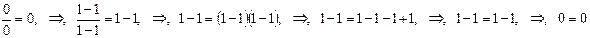
Оба примера доказывают, что не только выражение 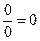верно, но и что число 0 является не только натуральным числом, но и единственно действенным натуральным числом.

Здесь мы, наконец, достигли пределов математики постоянных величин.

***

И вот теперь, как же быть с тем, что для неких целей в свое время было введено Эйлером в математику, а именно, вот с этим чудовищем[2]: 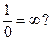И это – при царившем в его время запрещении делить на ноль?! Не был ли он умалишённым? Нет! Что позволено Юпитеру, не позволено быку! Он был высочайшим чиновником, а так как всякий чиновник – буквоед, самодур, то и самодуром. После всего сказанного должно стать ясно, что это представляет собой по своему существу смесь несмешиваемого, химеру, а по способу получения бесконечно большого числа – жульничество с нулём.

Действительно: 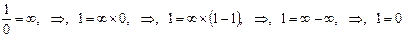Но, что может означать чисто количественное выражение 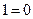, как оно здесь получено, абсолютно, кроме смеси несмешиваемого, химеры? Разве ноль количественно равен единице? Нет. Выражение 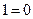, как оно содержится в выражении 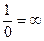, – химера чистой воды, тогда как, следовательно, само выражение 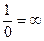– призрачное вольтерьянское бюрократически-химерическое чудовище.

Выше мной было получено действительное противоречие, качественное равенство, тождество противоположностей, 1 = 0, именно в силу того, что 2 = 2, т.е. для того случая, когда по своему эффекту в качестве делителей для числа 2 как 1, так и 0 оказались качественно равны между собой. И далее мной было показано, как это противоречие разрешается и во что именно оно разрешается. У Эйлера же ничего подобного и в помине нет. Здесь противоречие 1 = 0 выявлено количественно и безотносительно к чему бы то ни было, абсолютно, именно как лишённое всякого смысла вечное и неразрешаемое противоречие, как нелепое противоречие, как химера [3] , и Эйлером эта химера, произвольно и вольтерьянски, волюнтаристски им полученная путем суррогатной индукции и жульнического [4] «пренебрежения к малости разности», октроирована математике в синкретинической форме 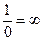. Voilà.

Получить бесконечно большую величину можно без жульничества с нулём вот, напр., таким путем:

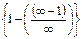Выражение представляет собой пример действительно бесконечно-малой

величины, отличной от нуля в строгом математическом смысле, величины, прообраз которой существует в реальности подобно тому, как существует в реальности и прообраз бесконечно большой величины, 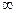, весь наш мир, вместе взятый с количественной стороны, из которого мы исходим в своих исследованиях как из безусловной предпосылки, и которую, собственно, и изучаем, а вместе с тем изучая самих себя.

Вообще говоря, попытка выведения бесконечно большого числа посредством «деления на ноль» представляет собой попытку вывести что-нибудь из ничего, представляет собой попытку продемонстрировать акт «божественного творения» посредством – как это сейчас видно – бессовестного жульничества с нулём на почве закрывания глаз (ведь только закрыв глаза на это нельзя этого не увидеть!) действительные противоречия, выявленные выше. Но ex nihilo nihil fit. Ничего из ничего не происходит. Что-нибудь происходит из чего-нибудь. Таков вывод из исторического опыта всего нашего естествознания по состоянию на текущий момент, в особенности, с того времени, когда был открыт закон неуничтожимости движения в форме закона превращения движения из одной формы в эквивалентных отношениях в другую, напр., механического движения в теплоту, магнетизм, и т.д., а именно, с середины XIX века.

А между тем призрачное бюрократически-химерическое чудовище, 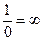, до сего дня ведёт своё паразитическое существование в математике, напр., в теории пределов, и в замаскированном виде заложено в основу так называемого «доказательства второго замечательного предела». Все это, поэтому, требует коренного пересмотра и очищения, приведения к соответствию действительности.

***

Из всего вышесказанного вытекает простой до очевидности вывод: делить любое число на 0 можно, но разделить такое число на 0 не возможно вообще; оно, это число, в итоге окажется неразделенным, рòвно таким же по величине, каким оно было изначально.

Непонимание всего вышеизложенного привело официальную математику в итоге к бюрократически тупорылому запрещению деления на ноль в области постоянных величин вместо хотя бы интуитивного указания на то обстоятельство, что деление на ноль имеет нулевой результат: делимое (сокращаемое) число оказывается в итоге не разделенным (не сокращённым) точно также, как при делении (сокращении) этого числа на единицу. Но бюрократ чувствует, что тут он носом утыкается в действительное противоречие, с которым он в силу присущего ему профессионального кретинизма не знает, что делать, бессилен перед ним, а потому стремится всеми фибрами своей души, когда оно во весь рост встаёт перед ним, замаскировать, спрятать его, откреститься от него. Для бюрократа важно запретить то, что он не понимает, а не делать попытки разобраться в вопросе. Он понимает только язык инструкций, протоколов. А когда же бюрократ попадает в тупик перед необходимостью таки в вопросе разбираться, то он делает это в соответствии со своей природой и по пути наименьшего сопротивления. А из этого образа действия, как мы видели выше, вытекают наихудшие из противоречий, нелепые, недействительные противоречия сумасбродной головы бюрократа, призрачные химерические чудовища, которые он в конце-концов вынужден … признать «значимыми» в силу своего собственного «общественного авторитета» или «общественного авторитета» себе подобного, себе равного или более высокого по рангу, того «академика», который «высочайше» октроирует обществу свои перлы и требует безропотного признания этого сумасбродства. Результаты же теоретического сумасбродства бюрократа «от науки» в силу необходимой связи теории и практики, мышления и практического действия должны по необходимости иметь и имеют следствия аналогичного свойства в практической жизни общества, ответственность за которые в современном обществе обычно ложится на плечи рабочего класса. Не удивительно, поэтому, царящее в рабочем классе оправданное практикой интуитивное недоверие, доходящее до степени презрения, к этим «академикам».

С.Н. Водянов[5], Кузбасс, 2023 г.

[1] на деле мы также равенство в равенстве подвергли отрицанию путем выяснения того, что как 1, так и 0 в качестве делителей по своему эффекту равны между собой.

[2] «§83. … Поелику дробь 1/∞ показывает частное, происходящее от деления 1 на ∞, и мы знаем также, что когда делимое 1 на частное число 1/∞ или 0, как прежде мы видели, разделится, то выйдет делитель ∞, и из сего получаем мы новое понятие о бесконечности, а именно, что оная происходит от разделения 1 на 0; чего ради по справедливости сказать можно, что 1, разделенная на 0, означает бесконечно великое число, или ∞...» («Оснований алгебры Леонарда Эйлера части первой первыя три отделения, переведенныя с французского языка на Российской, со многими присовокуплениями, Василием Висковатовым, Академии Наук Экстраординарным Академиком», 1812 г., стр. 51)

[3] Эта чисто количественная химера, 1 = 0, хотя и в форме , была получена Эйлером при разложении в бесконечный ряд его суррогатной неправильной дроби вида , дроби, полученной им путем суррогатной индукции из трех не имеющих между собой никакой связи общих случаев, когда a > m, когда a = m и когда a < m. Найдя, что в случае a > m получение бесконечного ряда связано «с огромнейшими несообразностями» (см. §103 «Оснований алгебры…»), он оставил эту «загадку» решать своим ученикам, не заметив, что в этом случае положительная неправильная дробь превращается в отрицательную правильную, , а тем самым вскрывается суррогатный характер его неправильной дроби . А между случаями, когда a = m и когда a < m он устанавливает «мост» путем итогового «пренебрежения малостью» разности (m – a ) , т.е. путем итогового произвольного приравнивания конечной разности (m – a ) к нулю, приравнивания, которое по сути дела есть следствие положения конца бесконечному поступенному приближению величины a к величине m, в форме a = m, что нелепо потому, что такое приближение в действительности ассимптотично: величина a ни при каких условиях не может быть равна величине m ; это – абсолютный закон бесконечного приближения, ассимптотизма. Таким путем у Эйлера и получается чёрт, , и, как частный случай, его «производная», его малютка, настоящее чудовище: . (см. §107 «Оснований алгебры…»). Вот уж, право слово, и в самом деле: не так «страшен» чёрт, как его малютка.

Действительно, случай (a > m ) - это самостоятельный случай отрицательной правильной дроби , и он относится к теме не неправильных, а правильных дробей; случай ( a = m ) – это рассмотренный мной в самом начале особенный случай , и только случай ( a < m ), когда величина a есть правильная дробь, является случаем, адекватным стоящей перед нами задачи поступенного разложения в бесконечный ряд отношения с конечной разностью (m – a ), разложения, определяемого, в общем и целом, отношением . И это последнее только в таком контексте является действительно всеобщим случаем для трёх особенных и внутренне зависимых. К примеру, при m = 1 в общем случае могут быть рассмотрены следующие три особых случая a:

когда (случай для поступенного бесконечного увеличения), когда (случай для поступенного бесконечного уменьшения), и когда (случай для бесконечного «топтания» на месте.). Разумеется, в таком общем случае, , в знаменателе разность (1 – a) конечная и невычисляемая, а величины m и x – натуральные числа больше нуля.

Таким образом, под ликом сумасбродного чудовища , скрываются реальные качественно различные и внешне самостоятельные, но внутренне связанные между собой бесконечные отношения.

[4] а бюрократ (чиновник, управленец), в особенности российский бюрократ – а Эйлер был российским чиновником «от науки», – он не мелочится, не «тырит мелочь по карманам», он по своей природе жулик, так сказать, промышленного масштаба!

[5] Рабочий и работница! Познакомившись и разобравшись с данной работой поделись ей с товарищем, помоги ему (ей) разобраться в этом, если он(а) слаб(а)! Интеллектуальные силы рабочего класса неисчерпаемы! Пусть в среде рабочего класса зреет сознание презрения и ненависти к «академикам», оплачиваемым буржуазией и одурачивающим рабочий класс, в частности, и к классу буржуазии, этому поработителю и угнетателю, в целом! Нет и не может быть в мире силы, способной сломить волю и стремление к знаниям, свободе и жизненному благополучию объединённых и организованных в свой собственный класс для взятия своей судьбы в свои руки масс рабочих всего мира! Рабочий класс способен не только на то, чтобы вырвать из лап буржуазии науку, очистить ее от бюрократического хлама и поставить ее себе на службу.

Для осуществления такого рода деятельности, деятельности по защите интересов рабочего класса, я нуждаюсь не только в духовной, но и в финансовой поддержке.

Мои координаты: Wodjanow@mail.ru, +7 (953) 858 49-65, Сбербанк, 4817 4602 7746 0527