Действительно: Но, что может означать чисто количественное выражение , как оно здесь получено, абсолютно, кроме смеси несмешиваемого, химеры? Это – она и есть.
|
Действия с нулём
(разоблачение математического жульничества с нулём)
Если две качественно различные «вещ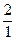и» 
и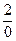 
порознь равны третьей, 2, то они равны между собой. Следовательно, 
.
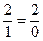Данный вывод кажется невероятным, хотя и является полученным на основе логического закона.
Теперь. Если наши предпосылки верны, если мы к ним правильно применяем законы мышления, то и результат должен соответствовать действительности. Посмотрим, поэтому, как у нас дело обстоит на практике.
Спросим себя, каким будет результат, если некое число сократить (разделить) количеством величиной в 1? Произведя расчет, получим, что сокращаемое (делимое) число окажется не сокращённым (не разделенным). Каким оно было перед началом сокращения (деления), таким оно и остается в итоге, 2 = 2. А каким будет итог, если мы то же самое число сократим (разделим) в 0 раз? Правильно. Итог будет тем же, что и в предыдущем случае, 2 = 2. Следовательно, в данном случае по своему эффекту в качестве делителей как 0, так и 1 качественно равны между собой: 1 = 0. Последнее равенство является не количественным, а качественным; оно есть действительное противоречие, не устранимое по свое природе, и возникает всякий раз в аналогичных ситуациях. И в самом деле, сократим ли мы исходное число 2 в 1 раз или в 0 раз, результат будет одним и тем же, число не станет сокращенным (не станет разделенным), останется равным самому себе,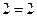 
. Стало быть и на деле[1]: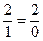
Следовательно, тот результат, который был получен число логически, у нас совпадает с чисто практическим результатом. А отсюда следует, далее, что и наши изначально взятые теоретические предпосылки верны.
Из качественного отношения равенства 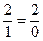, основой которого является количественное равенство исходного пункта и конечного результа, 2 = 2, равенство, полученное диаметрально противоположными способами, вовсе не вытекает чисто количественное отношение: 
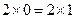. Такая нелепица может получиться только у того, кто из-за абстрактного, чисто количественного рассмотрения забывает о качественных различиях. На деле последнее отношение не может вытекать из первого. В последнем случае 0 и 1 играют качественно иную роль, чем в первом случае, а именно, роль не делителей, а роль множителей. А в своей функции множителей числа 1 и 0 качественно не равны друг другу. Поэтому, отношение, представляющее собой действительное, реально существующее противоречие, 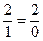при превращении 0 и 1 из делителей в множители, распадается – подобно делению органической клетки – на два внешне самостоятельных, но внутренне зависимых друг от друга чисто количественных отношения:
.
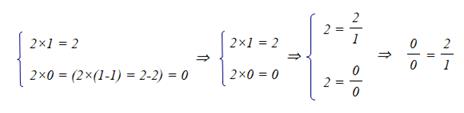Как становится видно, противоречие выражения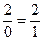 
разрешается в выражении 
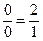тем, что последнее само собой вытекает из первого в результате нашего превращения 1 и 0 из делителей в множители. Это – отрицание отрицания.
Кто станет отрицать, что если мы некую величину попытаемся умножить в ноль раз, то она не станет умноженной? Тоже самое касается и умножения на 1. И всё же число ноль в отличие от единицы по своей природе есть особенное число; оно по своему происхождению является невычисляемой конечной разностью, зафиксированной по общечеловеческому соглашению в положительной форме особого числа, 0, а его природа может быть выражена, напр., таким образом: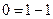 
. И ноль, взятый в функции множителя, он, аналогично единице, действительно не умножает никакого числа. Но в отличие от единицы он, наоборот, взятый в функции множителя, всякое число уничтожает, превращает его в себе количественно равное. Взятый же в функции делителя, ноль бессилен точно также, как и взятая в этой же функции единца. Это – то внутреннее неистребимое противоречие нуля, в которое он впадает, когда его используют в рамках математического уровня умножения и деления в силу своей внутренне противоречивой природы невычисляемой конечной разности. Здесь, как и везде, требуется не затушёвывать, скрывать, прятать неистребимые естественные противоречия, а затем жульничать с ними, а выявлять их и учиться ими пользоваться для достижения правильных, адекватных природе результатов.
Таким образом из всего вышесказанного вытекает простой до очевидности вывод: делить любое число на 0 можно, но разделить такое число на 0 не возможно вообще; оно, это число, в итоге окажется неразделенным, рòвно таким же по величине, каким оно было изначально.
Непонимание всего вышеизложенного привело математиков в итоге к бюрократически тупорылому запрещению деления на ноль, вместо хотя бы интуитивного указания на то обстоятельство, что деление на ноль имеет нулевой результат: делимое (сокращаемое) число оказывается в итоге не разделенным (не сокращённым) точно также, как при делении (сокращении) этого числа на единицу. Но бюрократ чувствует, что отсюда возникает противоречие, с которым он в силу присущего ему профессионального кретинизма не знает, что делать, бессилен перед ним, а потому стремится всеми фибрами своей души его спрятать. А отсюда, как мы увидим ниже, вытекают нелепые, сумасбродные противоречия, настоящие чудовища, которые он в конце-концов вынужден признать, но не потому, что он понимает это, а в силу «общественного авторитета» того, кто требует признания этого.
И вот теперь, как же быть с тем, что для неких целей в свое время было введено Эйлером в математику, а именно, вот с этим чудовищем[2]: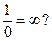 
После всего сказанного ясно, что это представляет собой по своему существу смесь несмешиваемого, химеру, а по способу получения бесконечно большого числа – жульничество с нулём.
Действительно: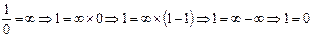 
Но, что может означать чисто количественное выражение 
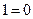, как оно здесь получено, абсолютно, кроме смеси несмешиваемого, химеры? Это – она и есть.
Выше мной получено действительное противоречие, качественное отношение 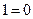именно потому, что 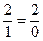, т.е. для того случая, когда по своему эффекту в качестве делителей для числа 2 как 1, так и 0 оказались качественно равны между собой. У Эйлера же ничего подобного и в помине нет. Здесь оно получено количественно и безотносительно к чему бы то ни было, абсолютно именно как химера, как 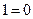, и Эйлером это произвольно, волюнтаристски постулировано в форме чудовища 
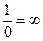. Voilà.
Получить бесконечно большую величину можно без жульничества с нулём вот, напр., таким путем:
 | |
 |
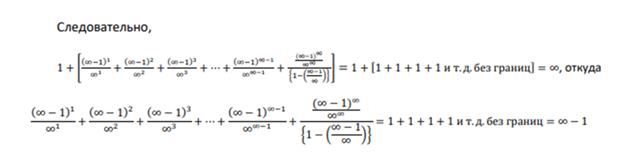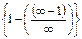Выражение представляет собой пример действительно бесконечно-малой
величины, отличной от нуля в строгом математическом смысле, величины, аналог которой существует в реальности подобно тому, как существует в реальности и бесконечно большая величина,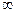 
, весь наш мир вместе взятый с количественной стороны, из которого мы исходим в своих исследованиях как из безусловной предпосылки, которую, собственно, и изучаем, а вместе с тем изучая самих себя.
Вообще говоря, попытка выведение бесконечно большого числа посредством «деления на ноль» представляет собой попытку вывести что-нибудь из ничего продемонстрировать акт «божественного творения» посредством, – как это сейчас видно – бессовестного жульничества с нулём на почве сокрытия действительного противоречия, выявленного выше. Но ex nihilo nihil fit. Ничего из ничего не происходит. Таков вывод из исторического опыта всего нашего естествознания по состоянию на текущий момент, в особенности, с того времени, когда был открыт закон неуничтожимости движения в форме закона превращения движения из одной формы в эквивалентных отношениях в другую, напр., механического движения в магнетизм, электричество, и т.д., а именно, с середины XIX века.
А между тем бюрократически-химерическое чудовище, 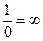, до сего дня используется в математике, в теории пределов, и заложено в основу так называемого «доказательства второго замечательного предела».
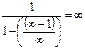Фактически же мы имеем дело не с химерой, 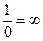, а с правильным отношением, напр., вот с таким:
С.Н. Водянов, Кузбасс, 2023 г.
[1] на деле мы также выражение в выражении подвергли отрицанию путем выяснения того, что как 1, так и 0 в качестве делителей по своему эффекту равны между собой.
[2] «§83. … Поелику дробь 1/∞ показывает частное, происходящее от деления 1 на ∞, и мы знаем также, что когда делимое 1 на частное число 1/∞ или 0, как прежде мы видели, разделится, то выйдет делитель ∞, и из сего получаем мы новое понятие о бесконечности, а именно, что оная происходит от разделения 1 на 0; чего ради по справедливости сказать можно, что 1, разделенная на 0, означает бесконечно великое число, или ∞...» («Оснований алгебры Леонарда Эйлера части первой первыя три отделения, переведенныя с французского языка на Российской, со многими присовокуплениями, Василием Висковатовым, Академии Наук Экстраординарным Академиком», 1812 г., стр. 51)