Оценивание параметров случайной величины

Дата: 2025-06-02; Просмотры: 11
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Цель работы

 

Получение навыков оценивания параметров случайных величин с использованием возможностей табличного процессора

Порядок выполнения работы

Задание

Пусть случайная величина Х – сведения о ежедневной прибыли кафе (в тысячах рублей), которое проработало 60 дней.

Извлечь из генеральной совокупности случайную выборку из 25 элементов. Для этой выборки рассчитать:

Сделать выводы.

Выполнение работы

  1. Создайте новую книгу MS Excel;
  2. На первом листе с помощью генерации случайных чисел создадим данные для генеральной совокупности. Для этого выполните следующие действия:
    1. На первом листе в первом столбце А проставьте нумерацию от 1 до 60.
    2. Вызовите пункт меню Сервис/Анализ данных…
    3. В открывшемся диалоговом окне выберите Генерация случайных чисел, нажмите кнопку ОК;
    4. В открывшемся диалоговом окне установите следующие параметры: число переменных – 1; число случайных чисел – 60; распределение – нормальное; среднее – 150; стандартное отклонение – 10; выходной интервал – В1. Нажмите ОК.
  3. Получим случайную выборку из 25 элементов: их нужно случайным образом отобрать из полученных 60 данных генеральной совокупности. Для этого выполните следующие действия:
    1. Вызовите пункт меню Сервис/Анализ данных…
    2. В открывшемся диалоговом окне выберите Выборка, нажмите кнопку ОК.
    3. В открывшемся диалоговом окне задайте следующие параметры: входной интервал – В1:В60; метод выборки – случайный; число выборок – 25; выходной интервал D1. Нажмите ОК.
  4. Выделите столбец D и отсортируйте его по возрастанию.
  5. Сделайте заготовки таблиц для последующих вычислений (см. рисунок). Внимание: случайные числа в вашей работе будут отличаться от тех, что на рисунке!

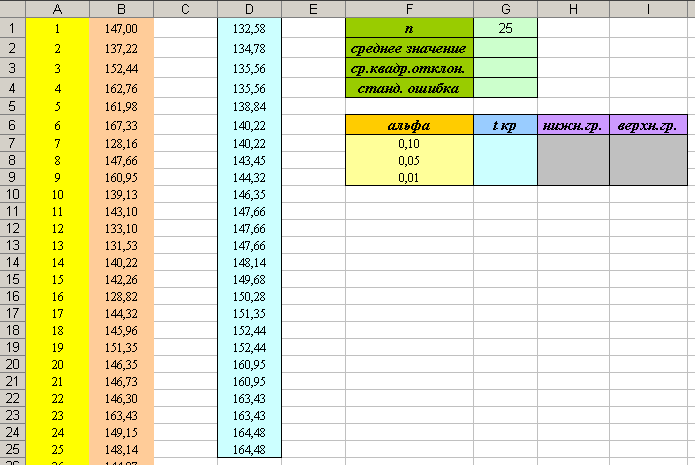
  1. В ячейке G2 вычислите среднее значение для диапазона D1:D25, используя функцию СРЗНАЧ ( ).
  2. В ячейке G3 вычислите среднее квадратическое отклонение для диапазона D1:D25, используя функцию СТАНДОТКЛОН ( ).
  3. Вычислим стандартную ошибку по формуле 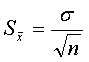. Установите курсор в ячейку G4 и введите формулу: =G3/КОРЕНЬ(G1).
  4. Вычислим критические точки. Установите курсор в ячейку G7 и введите формулу: =СТЬЮДРАСПОБР(F6;24). Скопируйте эту формулу вниз, в ячейки G8 и G9.
  5. Вычислим границы доверительных интервалов (границы доверительных интервалов находятся из формулы ).
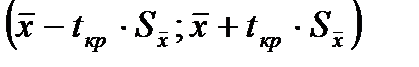    1. Установите курсор в ячейку Н7 и введите формулу: =$G$2-G7*$G$4.
    2. Установите курсор в ячейку I7 и введите формулу: =$G$2+G7*$G$4.
    3. Скопируйте формулы из ячеек Н7 и I7 на две строки вниз.
  6. Вы должны получить следующую таблицу:

Внимание: значение случайных чисел, среднего арифметического, среднего квадратического, стандартной ошибки и границ доверительных интервалов в вашем файле будут отличаться от тех, что приведены на рисунке; значения критических точек должны совпадать.

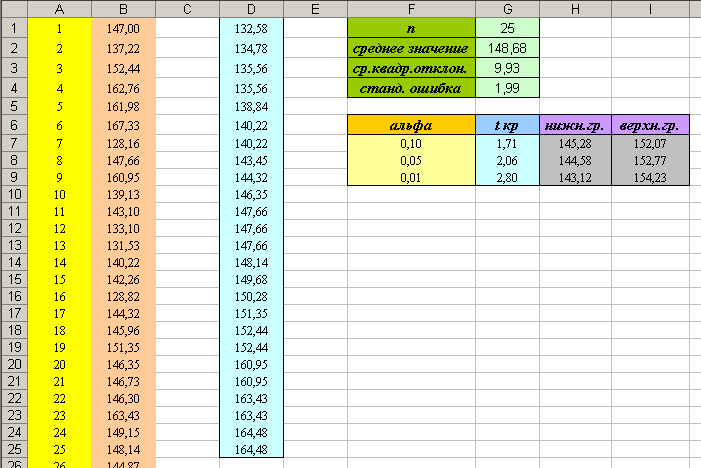
На основании данных, приведённых на рисунке, можно сделать следующие выводы:

Сделайте аналогичные выводы для ваших данных.

 

Контрольные вопросы

  1. Для чего используется стандартная ошибка? Что она позволяет оценить?
  2. Что такое доверительный интервал?
  3. Как найти доверительный интервал для математического ожидания?
  4. Как определить критическую точку распределения Стьюдента?
  5. Какие встроенные функции вы использовали при выполнении работы и для чего?

 

Дополнительное задание

  1. Из генеральной совокупности, полученной при выполнении работы, извлеките новую случайную выборку в 20 элементов;
  2. Для этой выборки вычислите:

· Выборочное среднее;

· Выборочное среднее квадратическое отклонение;

· Стандартную ошибку;

· Границы доверительных интервалов (с вероятностью 90%, 95% и 99%).

  1. Сделайте выводы. Сравните новые результаты с теми, что были получены ранее.

 

 

[1] Термин "регрессия" (regression (лат.) – отступление, возврат к чему-либо) ввел английский статистик Ф. Гальтон. Он исследовал влияние роста родителей и более отдаленных предков на рост детей. По его модели рост ребенка определяется наполовину родителями, на четверть – дедом с бабкой, на одну восьмую прадедом и прабабкой и т.д. Другими словами, такая модель характеризует движение назад по генеалогическому дереву. Ф. Гальтон назвал это явление регрессией как противоположное движению вперед – прогрессу. В настоящее время термин "регрессия" применяется в более широком плане – для описания статистической связи между случайными величинами.