Внимание! Значения ассиметрии и эксцесса могут отличаться от вычисленных по формуле!
19) Установите курсор в ячейку I9 и введите формулу: =6*I8/((I8+1)*(I8+3));
20) Установите курсор в ячейку I10 и введите формулу: =24*(I8-2)*(I8-3)*I8/((I8+3)*(I8+5)*((I8-1)^2));
21) Установите курсор в ячейку I11 и введите формулу: =3*КОРЕНЬ(I9);
22) Установите курсор в ячейку I12 и введите формулу: =5*КОРЕНЬ(I10);
Таблица должна выглядеть следующим образом:
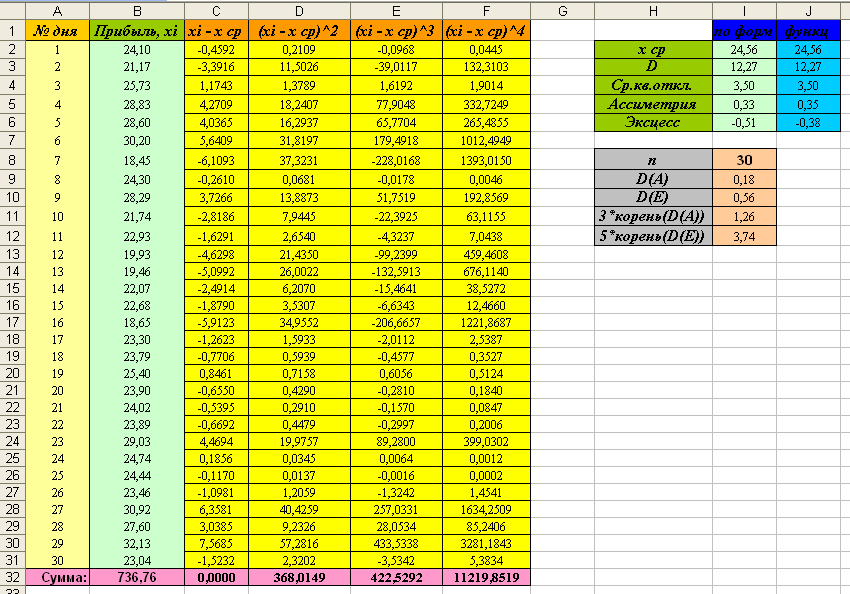
Из таблицы видно, что выполняются неравнества:
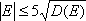и 
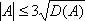
Следовательно, можно предположить, что распределение прибыли близко к нормальному.
II . Графический способ.
1) Скопируйте на второй лист во второй столбец данные о прибыли:
2) Отсортируйте этот столбец по возрастанию (пункт меню Данные /Сортировка…)
3) Создайте в первом столбце нумерацию по возрастанию (начиная со второй строки) и сделайте заготовки таблиц для последующих расчётов (см. рисунок):
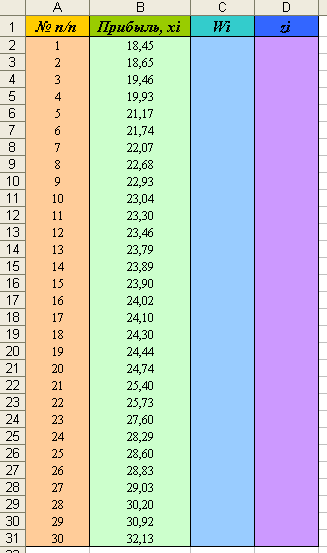
4) В третьем столбце вычислим накопленные частости по формул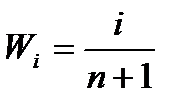е 
, где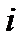 
- номер значения по порядку. Установите курсор в ячейку С2 и введите формулу: =A2/31. Скопируйте эту формулу вниз в диапазон ячеек С3:С31.
5) В четвёртом столбце вычислим значения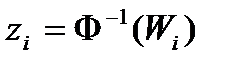 
. В таблице для стандартного нормального распределения для некоторого аргумента указывается вероятность того, что случайная величина окажется меньше этого аргумента. В данном случае нам требуется обратное: для заданной вероятности 
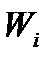найти значение аргумента 
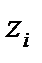. Для этого будем использовать специальную встроенную функцию. Установите курсор в ячейку D2 и введите формулу: =НОРМСТОБР(C2:C31). Скопируйте эту формулу вниз в диапазон ячеек D3:D31.
6) Если всё выполнено верно, вы должны получить следующую таблицу:
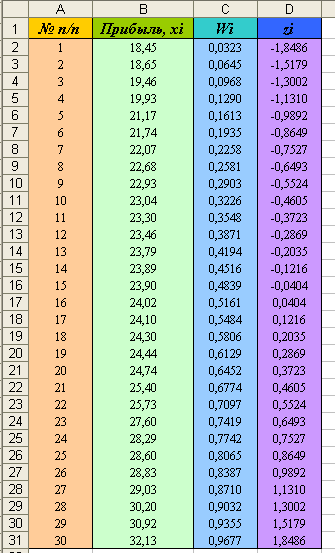
7) Построим график зависимости от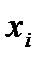 
- он должен быть близок к линейному. Выделите диапазон ячеек D2:D31 и вызовите пункт меню Вставка/Диаграмма. В открывшемся диалоговом окне выберите тип диаграммы – точечная, нажмите Далее. В новом диалоговом окне перейдите на вкладку Ряд и в поле Значения Х задайте диапазон В2:В31. Нажмите Готово. В настройках графика для шкалы ОХ задайте минимальное значение – 15. Выделив диаграмму, вызовите пункт меню Диаграмма/Добавить линию тренда. В открывшемся диалоговом окне выберите тип линии тренда линейная и нажмите ОК. Вы должны получить следующий график:
По графику видно, что зависимость 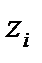от 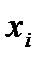похожа на линейную, следовательно, можно предположить, что изучаемое распределение подчиняется нормальному закону.
III. Сгруппируем данные, найдём моду, медиану и среднее значение и сравним эти величины между собой. Если они окажутся приблизительно равными, то можно сделать вывод о том, что распределение близко к нормальному.
1) Скопируйте на третий лист исходные данные и сделайте заготовки таблиц для последующих расчётов (см. рисунок):
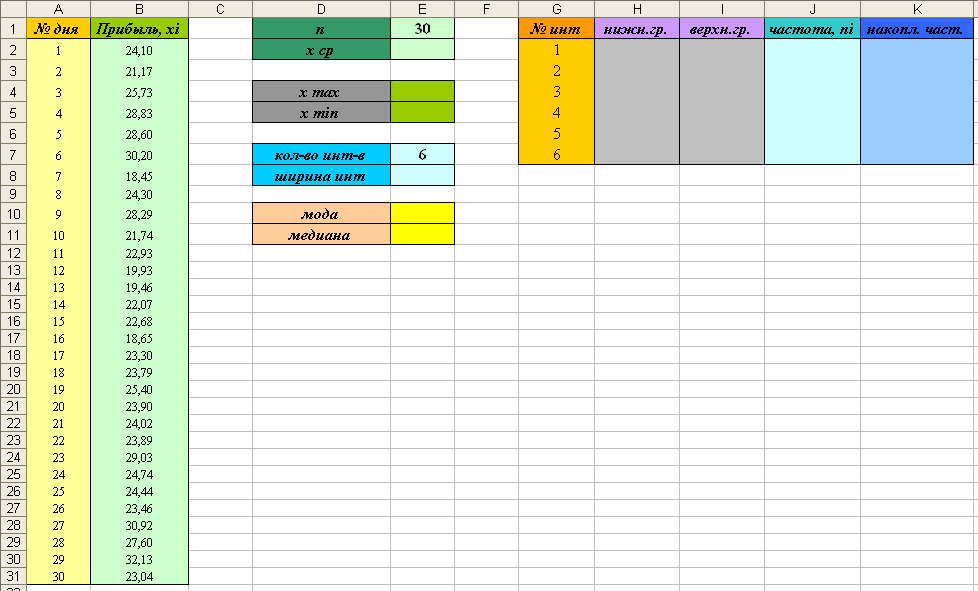
2) В ячейке Е2 вычислите среднее значение прибыли с помощью функции СРЗНАЧ ( );
3) Установите курсор в ячейку Е4 и введите формулу: =МАКС(B2:B31).
4) Установите курсор в ячейку Е5 и введите формулу: =МИН(B2:B31).
5) Количество интервалов возьмём равным 6. Расчитаем ширину интервалов по формуле: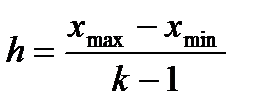 
. Установите курсор в ячейку Е8 и введите формулу: =(E4-E5)/(E7-1).
6) Найдём нижнюю границу первого интервала по формуле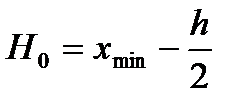 
. Установите курсор в ячейку Н2 и введите формулу: =E5-E8/2.
7) Найдём верхнюю границу первого интервала, прибавив к нижнее границе ширину интервала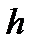 
. Установите курсор в ячейку I2 и введите формулу: =H2+$E$8.
8) Нижняя граница второго интервала равна верхней границе первого, поэтому в ячейку Н3 следует ввести формулу: = I2. В ячейку I3 скопируйте формулу из ячейки I2.
9) Выделите ячейки Н3: I3 и скопируйте формулы из них вниз в диапазон Н4: I7.
10) Подсчитаем частоту для каждого интервала (то есть, сколько значений попадет в каждый интервал) с помощью встроенной функции. Выделите диапазон J2: J7 и введите формулу: =ЧАСТОТА(B2:B31;I2:I6). Ввод формулы завершите, одновременно нажав клавиши CTRL, Shift и Enter. Внимание: посмотрите справку для функции ЧАСТОТА ( ) и самостоятельно разберитесь, почему именно так задаются аргументы.
11) В столбце К самостоятельно вычислите накопленные частоты.
12) Из столбца J мы видим, что модальным является интервал №3: в нём признак имеет набольшую частоты. Вычислим значение медианы по формуле:
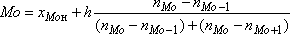
Установите курсор в ячейку Е10 и введите формулу: =H4+E8*(J4-J3)/((J4-J3)+(J4-J5)). (Встроенную функцию МОДА ( ) здесь не удасться использовать, так как она подходит только для несгруппированных рядов, в которых встречаются повторяющиеся значения признака).
13) Из столбца К мы видим, что медианным является так же интервал №3, так как для этого интервала накопленная частота впервые оказалась больше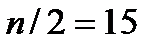 
. Установите курсор в ячейку Е11 и введите формулу: =МЕДИАНА(B2:B31).
14) Вы должны получить следующую таблицу:
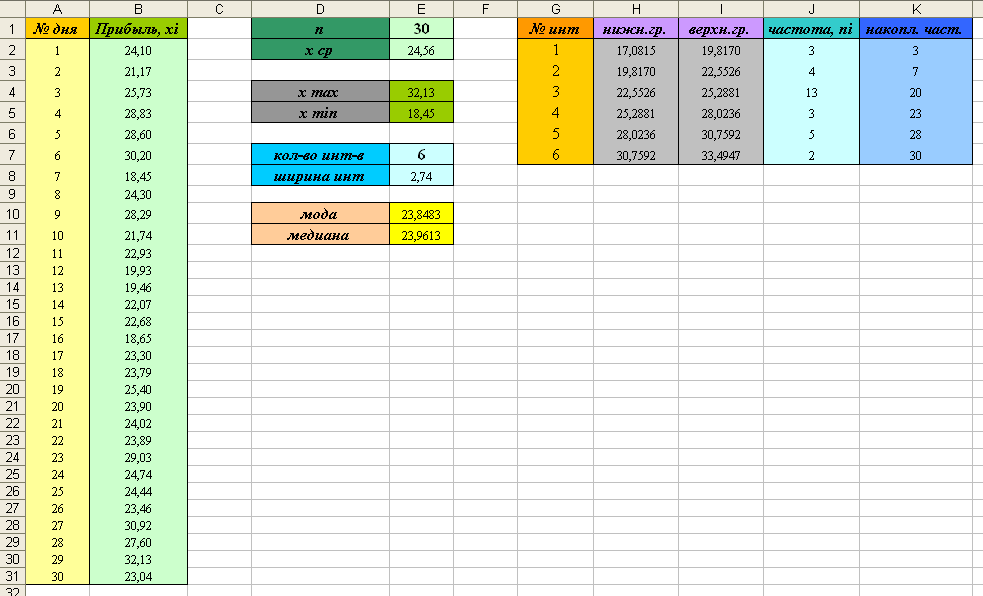
Из таблицы видно, что мода, медиана и среднее арифметическое имею близкие значения. Можно предположить, что распределение является нормальным.
Часть 2
I. Вернитесь на первый лист в файле с лабораторной работой. Создайте заготовки таблиц для последующих вычислений (см. рисунок):
Вероятность попадания нормально распределённой величины в заданный промежуток будем вычислять по формуле:
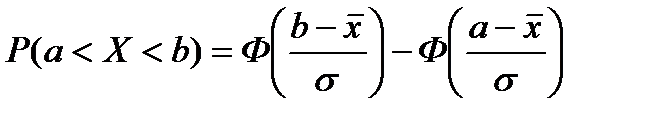
1) Установите курсор в ячейку N1 и введите формулу: =(L2-$I$2)/$I$4. Скопируйте эту формулу в ячейку вниз.
2) Установите курсор в ячейку О1 и введите формулу: =(M2-$I$2)/$I$4. Скопируйте эту формулу в ячейку О3.
3) Установите курсор в ячейку Р1 и введите формулу: =НОРМСТРАСП(N2). Скопируйте эту формулу в ячейку вниз.
4) Установите курсор в ячейку Q1 и введите формулу: =НОРМСТРАСП(O2). Скопируйте эту формулу в ячейку Q3.
5) Подсчитайте в столбце R нужные разности.
6) Вы должны получить следующую таблицу:
Из этой таблицы делаем выводы:
1) Вероятность того, чтобы прибыль магазина за день составит от 19 тыс. до 22 тыс. составляет 17,63%.
2) Вероятность того, что дневная прибыль магазина окажется больше 25 тыс. составляет 44,98%.
3) Вероятность того, что дневная прибыль магазина окажется меньше 19 тыс. составляет 5,63%.
Контрольные вопросы
- Какое распределение случайной величины называется нормальным?
- Что такое стандартное нормальное определение?
- Какими способами можно проверить, является ли распределение нормальным?
- Как найти вероятность попадания случайной величины в заданный интервал для нормального распределения?
- Какие специальные встроенные функции вы использовали при выполнении работы?
Дополнитнльное задание
- Создайте новую книгу MS Excel.
- Вызовите пункт меню Сервис/Анализ данных… В открывшемся диалоговом окне выберите Генерация случайных чисел и нажмите ОК.
- В открывшемся диалоговом окне задайте следующие параметры:
- Число переменных – 1;
- Число случайных чисел – 30;
- Распределение – нормальное;
- Среднее – номер студента по журналу;
- Стандартное отклонение – 0,5;
- Выходной интервал – А1.
- Нажмите ОК. В результате в диапазоне А1:А30 у вас будут помещены 30 случайных чисел, распределённых по нормальному закону. Для этих чисел:
- Всеми способами, которые использовались при выполнении лабораторной работы, докажите, что распределение является нормальным:
- Найдите следующие вероятности: величина находится в промежутке от К – 1 до К + 2; величина меньше К-5; величина больше 2К (К – последняя цифра номера зачетной книжки).
ЛАБОРАТОРНАЯ РАБОТА № 2д.