Частные уравнения регрессии
На основе линейного уравнения множественной регрессии могут быть найдены частные уравнения регрессии, то есть уравнения регрессии, которые связывают результативный признак у с соответствующими факторами xi при закреплении других, учитываемых во множественной регрессии, факторов на среднем уровне. Частные уравнения регрессии имеют следующий вид:
При подстановке в эти уравнения средних значений соответствующих факторов они принимают вид парных уравнений линейной регрессии.
В нашем случае:
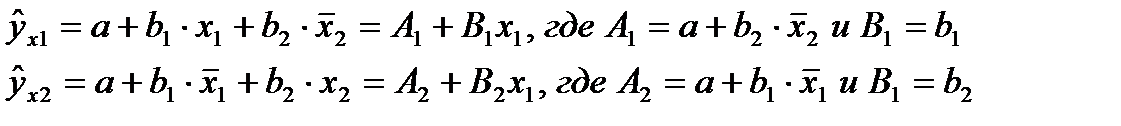
Параметры а, b1 и b2 – это параметры уравнения множественной регрессии.
- В книге MS Excel вернитесь на Лист1 (на этом листе было получено уравнение множественной регрессии). Создайте заготовки таблиц для вычислений (см. рисунок).
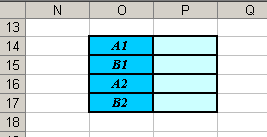
- В ячейке Р14 вычислите коэффициент А1, вставив формулу: =M10+M12*M23.
- В ячейку Р15 скопируйте значение из ячейки М11.
- В ячейке Р16 вычислите коэффициент А2, вставив формулу: =M10+M11*M22.
- В ячейку Р17 скопируйте значение из ячейки М17.
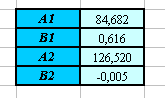
- Вы должны получить следующие результаты:
Вывод.
Частные уравнения регрессии имеют вид:
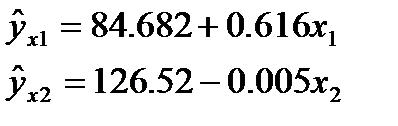
Частные индексы корреляции
Коэффициент частной корреляции (в случае линейной зависимости) измеряет влияние на результат у фактора xi при неизменном уровне других факторов и вычисляется по формуле:
, где
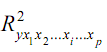- множественный коэффициент детерминации всего комплекса р факторов с результатом,
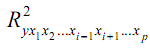- множественный коэффициент детерминации, но без введения в модель фактора хi.
В нашем случае:
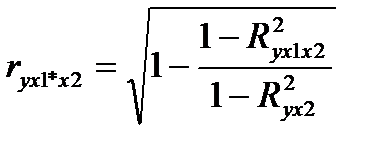- коэффициент частной корреляции, измеряющий влияние на результат Y фактора Х1 при неизменном уровне фактора Х2;
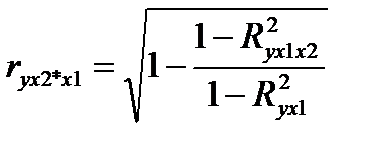- коэффициент частной корреляции, измеряющий влияние на результат Y фактора Х2 при неизменном уровне фактора Х1.
1. Перейдите в книге MS Excel на Лист 2 (на этом листе определялась значимость уравнения регрессии, на нём же находится матрица парных коэффициентов корреляции).
2. Создайте заготовки таблиц для последующих вычислений (см. рисунок)
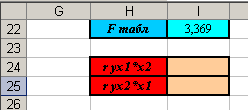
3. Вычислим коэффициент частной корреляции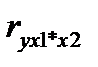 
. Установите курсор в ячейку I24 и введите формулу: =КОРЕНЬ(1-(1-I17)/(1-L5^2)).
4. Вычислим коэффициент парной корреляции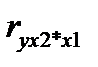 
. В ячейку I25 введите формулу: =КОРЕНЬ(1-(1-I17)/(1-L4^2)).
5. Вы должны получить следующие результаты:
Вывод:
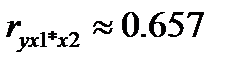- при неизменном значении фактора Х2 между фактором Х1 и результативным признаком Y присутствует достаточно сильная прямая зависимость.
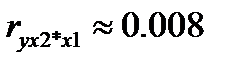- при неизменном значении фактора Х1 связь между факторным признаком Х2 и результативным признаком Y очень слабая, факторный признак Х2 практически не влияет на значение результата Y.